当前位置：首页 > news >正文

LeetCode 71~90题解

news 2025/8/7 13:21:57

LeetCode71.简化路径：

题目描述：

给你一个字符串 path ，表示指向某一文件或目录的 Unix 风格绝对路径（以 ‘/’ 开头），请你将其转化为更加简洁的规范路径。

在 Unix 风格的文件系统中规则如下：

一个点 ‘.’ 表示当前目录本身。
此外，两个点 ‘…’ 表示将目录切换到上一级（指向父目录）。
任意多个连续的斜杠（即，‘//’ 或 ‘///’）都被视为单个斜杠 ‘/’。
任何其他格式的点（例如，‘…’ 或 ‘…’）均被视为有效的文件/目录名称。
返回的简化路径必须遵循下述格式：

始终以斜杠 ‘/’ 开头。
两个目录名之间必须只有一个斜杠 ‘/’ 。
最后一个目录名（如果存在）不能以 ‘/’ 结尾。
此外，路径仅包含从根目录到目标文件或目录的路径上的目录（即，不含 ‘.’ 或 ‘…’）。
返回简化后得到的规范路径。

示例 1：

输入：path = “/home/”

输出：“/home”

解释：

应删除尾随斜杠。

示例 2：

输入：path = “/home//foo/”

输出：“/home/foo”

解释：

多个连续的斜杠被单个斜杠替换。

示例 3：

输入：path = “/home/user/Documents/…/Pictures”

输出：“/home/user/Pictures”

解释：

两个点 “…” 表示上一级目录（父目录）。

示例 4：

输入：path = “/…/”

输出：“/”

解释：

示例 5：

输入：path = “/…/a/…/b/c/…/d/./”

输出：“/…/b/d”

解释：

“…” 在这个问题中是一个合法的目录名。

提示：

1 <= path.length <= 3000
path 由英文字母，数字，‘.’，‘/’ 或 ‘_’ 组成。
path 是一个有效的 Unix 风格绝对路径。

思路：

利用栈思想将每个目录名字依次存入“栈”中，在遇到. .. //时进行对应操作选择入栈还是出栈还是不变（这题使用真实栈也可以做但是空间消耗可能大一些）

具体做法：将过程模拟一遍：形成思路
微信截图_20241120201500.png

时间复杂度：O(n)：每个字符遍历一次

注释代码：

class Solution {
public:string simplifyPath(string path) {string res;string name;  //记录文件路径名if(path.back() != '/') path += '/';  //以'/’为文件名的开始符，统一形式，减少特判条件for(auto c : path){if(c != '/'){name += c;cout<<name<<endl;}else{if(name == ".."){//返回上一级while(res.size() && res.back() != '/') res.pop_back(); //去掉文件名if(res.size()) res.pop_back(); //去掉'/'以便开始记录下一个路径名}else if(name != "." && name != ""){//.是本级目录， 空是重复/, 只要不是就可以将目录路径加入最终路径res += '/' + name;}name.clear();}}if(res.empty()) res = '/';return res;}
};

纯享版：

class Solution {
public:string simplifyPath(string path) {string res, name;if(path.back() != '/') path += '/';for(auto c : path){if(c != '/'){name += c;cout<<name<<endl;} else{if(name == ".."){while(res.size() && res.back() != '/') res.pop_back();if(res.size()) res.pop_back();} else if(name != "." && name != ""){res += '/' + name;}name.clear();}}if(res.size() == 0) res += '/';return res;}
};

LeetCode72.编辑距离：

题目描述：

给你两个单词 word1 和 word2，请返回将 word1 转换成 word2 所使用的最少操作数。

你可以对一个单词进行如下三种操作：

插入一个字符
删除一个字符
替换一个字符

示例 1：

输入：word1 = “horse”, word2 = “ros”
输出：3
解释：
horse -> rorse (将 ‘h’ 替换为 ‘r’)
rorse -> rose (删除 ‘r’)
rose -> ros (删除 ‘e’)

示例 2：

输入：word1 = “intention”, word2 = “execution”
输出：5
解释：
intention -> inention (删除 ‘t’)
inention -> enention (将 ‘i’ 替换为 ‘e’)
enention -> exention (将 ‘n’ 替换为 ‘x’)
exention -> exection (将 ‘n’ 替换为 ‘c’)
exection -> execution (插入 ‘u’)

提示：

0 <= word1.length, word2.length <= 500
word1 和 word2 由小写英文字母组成

##经典的动态规划思路题：如果第一时间没有反应过来说明DP问题做的少了（我就是。。。）

#思路：

动态规划：设定集合f[i, j]为a串的前[1_{i]个字符和b串的前[1}j]个字符匹配的最少操作次数：
###时间复杂度：O(n * n)

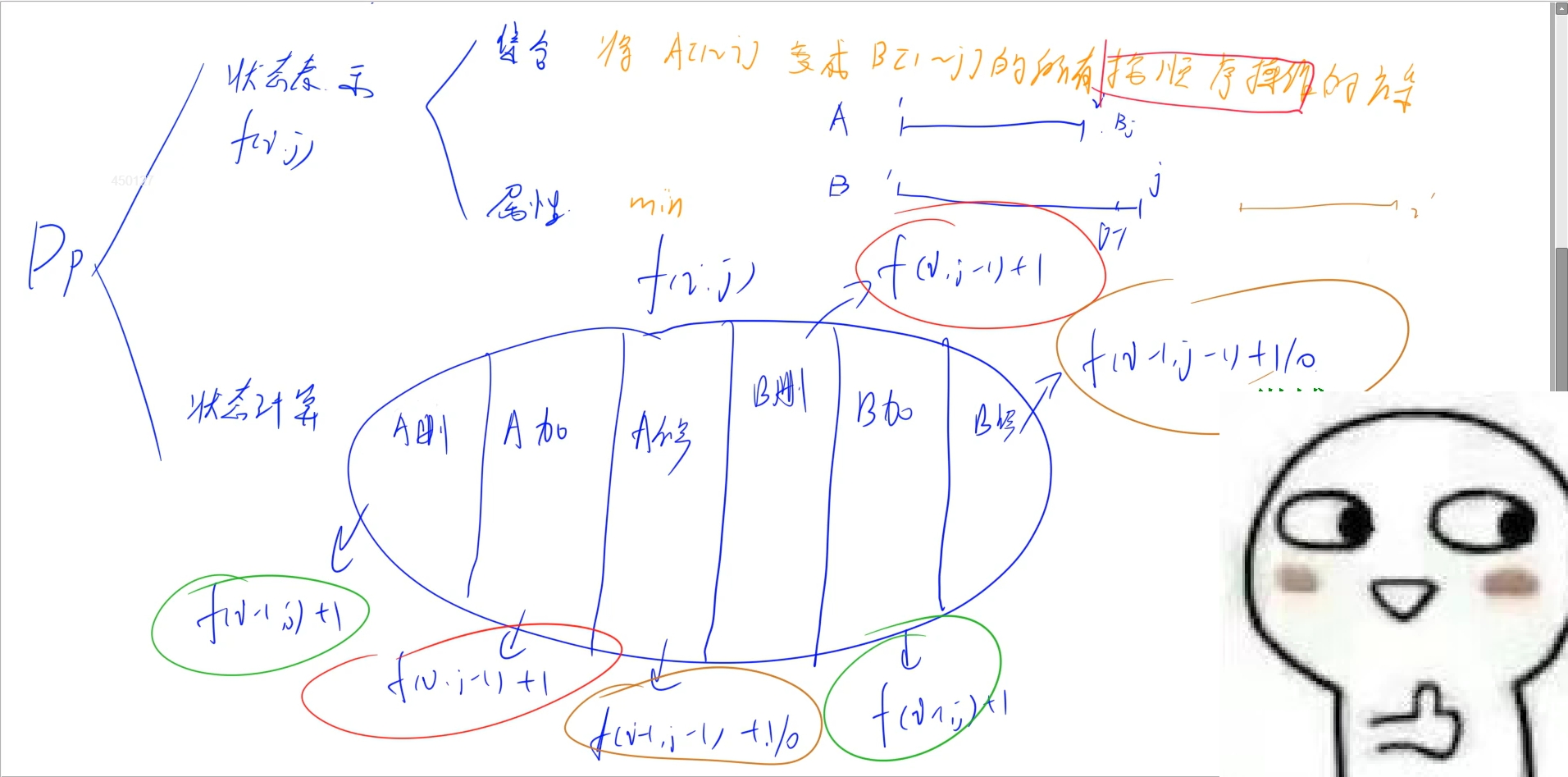
根据闫式DP分析法：集合：f[i, j]为a串的前[1_{i]个字符和b串的前[1}j]个字符匹配的最少操作次数，属性： min

0

集合划分：这里可以由两种看法：一种是a可以变成b，b可以变成a，那么就有六种集合划分方式： a删除一个字符、a修改一个字符、a插入一个字符、b删除一个字符、b修改一个字符、b插入一个字符
微信截图_20241120203321.png

0

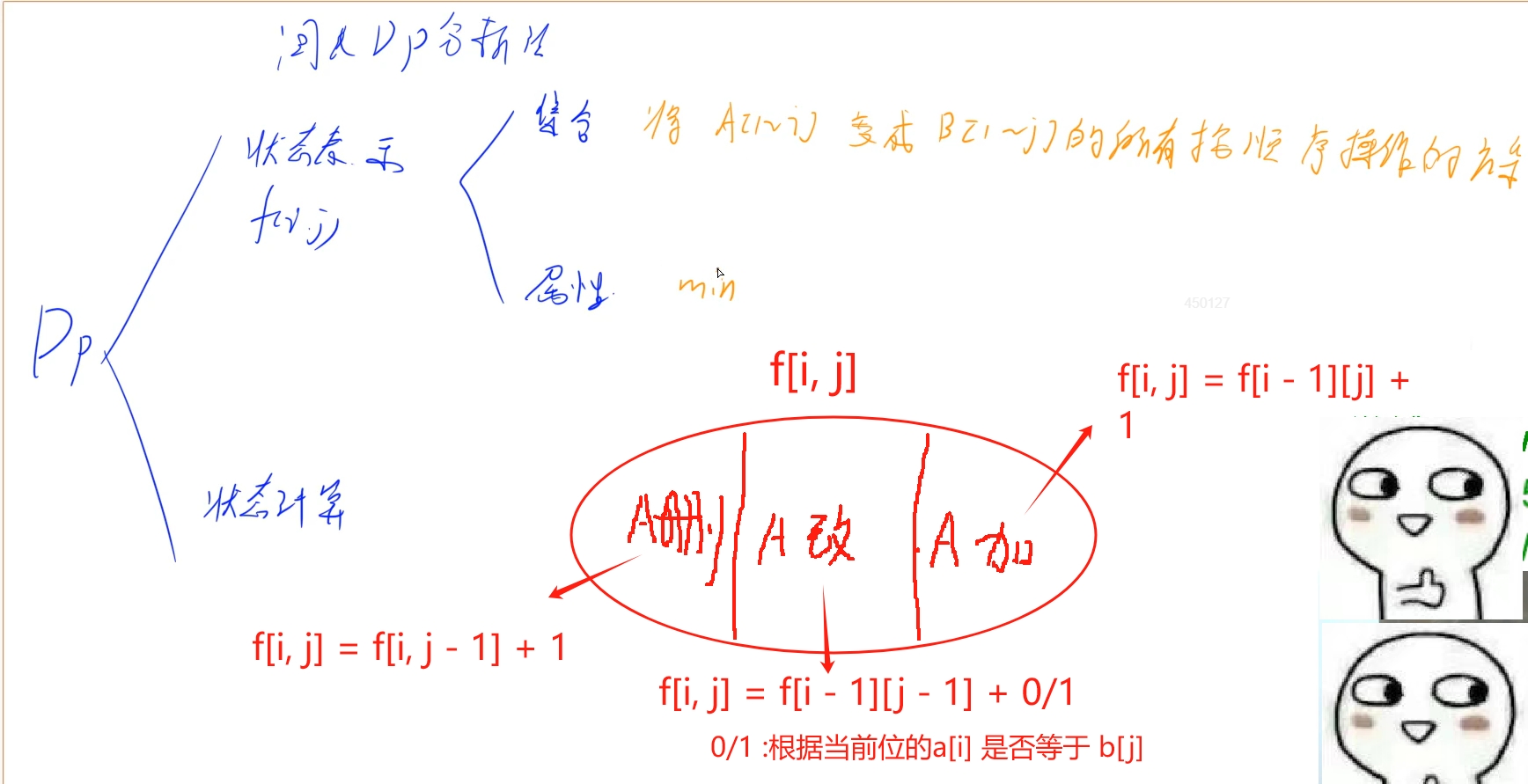
另外一种是因为a可以由b修改而来，或者a修改成b，那么选其中一个字符串向另外一个靠拢就相当于将二者其中一者修改成另外一者（题目意思也是只能对一个单词进行操作，而不能同时对两个进行修改），那么集合划分就是： a删除一个字符、 a改一个字符、 a加一个字符：对此状态转移方程分别对应：

1

当a删除一个字符才使得a串的前[1_{i]个字符和b串的前[1}j]个字符匹配，也就是说a串的前i - 1个字符和b串的前j个字符需要先匹配，然后进行一次删除操作得到：f[i][j] = f[i - 1][j] + 1;
###当a修改一个字符才使得a串的前[1_{i]个字符和b串的前[1}j]个字符匹配，也就是说a串的前i - 1个字符和b串的前j - 1个字符需要先匹配，然后判断当前也就是a[i] 是否等于b[j]，如果相等则无需操作，如果不等那么需要进行一次修改操作得到：f[i][j] = f[i - 1][j - 1] + 0/1;

2

当a增加一个字符才使得a串的前[1_{i]个字符和b串的前[1}j]个字符匹配，也就是说a串的前i个字符和b串的前j - 1个字符需要先匹配，然后进行一次增加操作得到：f[i][j] = f[i][j - 1] + 1;

微信图片编辑_20241120210237.jpg

注释代码：

class Solution {
public:int minDistance(string a, string b) {int n = a.size(), m = b.size();a = ' ' + a, b = ' ' + b; //从1开始操作vector<vector<int>> f(n + 1, vector<int> (m + 1));//初始化//当b为空串时， 将a变成b只有将a都删除，或者插入a相同的字符，那么操作数都为a串的长度for(int i = 0; i <= n; i++) f[i][0] = i; for(int i = 0; i <= m; i++) f[0][i] = i;for(int i = 1; i <= n; i++){for(int j = 1; j <= m; j++){f[i][j] = min(f[i - 1][j], f[i][j - 1]) + 1;int t = a[i] != b[j]; //在a的前[1~i]和b的前[1~j]个字符已经匹配的前提下，如果a[i] == b[j] 那么就不需要再操作t= 0,否则t = 1f[i][j] = min(f[i][j], f[i - 1][j - 1] + t);}}return f[n][m];}
};

纯享版：

class Solution {
public:int minDistance(string a, string b) {int n = a.size(), m = b.size();a = ' '  + a, b = ' ' + b;vector<vector<int>> f(n + 1, vector<int>(m + 1));for(int i = 0; i <= n; i++) f[i][0] = i;for(int i = 0; i <= m; i++) f[0][i] = i;for(int i = 1; i <= n; i++){for(int j = 1; j <= m; j++){f[i][j] = min(f[i - 1][j], f[i][j - 1]) + 1;int t = a[i] != b[j];f[i][j] = min(f[i][j], f[i - 1][j - 1] + t);}}return f[n][m];}
};

LeetCode73.矩阵置零：

题目描述：

给定一个 m x n 的矩阵，如果一个元素为 0 ，则将其所在行和列的所有元素都设为 0 。请使用原地算法。

示例 1：
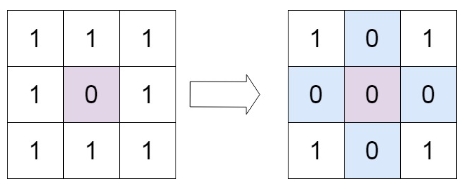
微信截图_20241121210725.png

输入：matrix = [[1,1,1],[1,0,1],[1,1,1]]
输出：[[1,0,1],[0,0,0],[1,0,1]]

示例 2：

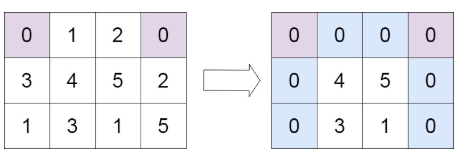
微信截图_20241121210732.png
输入：matrix = [[0,1,2,0],[3,4,5,2],[1,3,1,5]]
输出：[[0,0,0,0],[0,4,5,0],[0,3,1,0]]

提示：

m == matrix.length
n == matrix[0].length
1 <= m, n <= 200
-2^31 <= matrix[i][j] <= 2^31 - 1

进阶：

一个直观的解决方案是使用 O(mn) 的额外空间，但这并不是一个好的解决方案。
一个简单的改进方案是使用 O(m + n) 的额外空间，但这仍然不是最好的解决方案。
你能想出一个仅使用常量空间的解决方案吗？

思路：

首先这里需要做一个思想转换：题目意思是出现0的位置所在行和列都全置为0，如果挨个元素进行判断可能非常繁琐且难以实现，我们就需要换位思考一下，每个位置上的数什么情况下是0，什么情况下不为0：当元素所在行或者列为零的时候它就为0，那么我们就可以考虑每一行每一列是否存在有0的情况，因为要使用原地算法，不开额外的空间，使用两个变量r0和c0记录第一行和第一列中是否存在0，而第一行上的每一个数分别记录对应行是否存在0，第一列上的每一个数分别记录对应列是否存在0

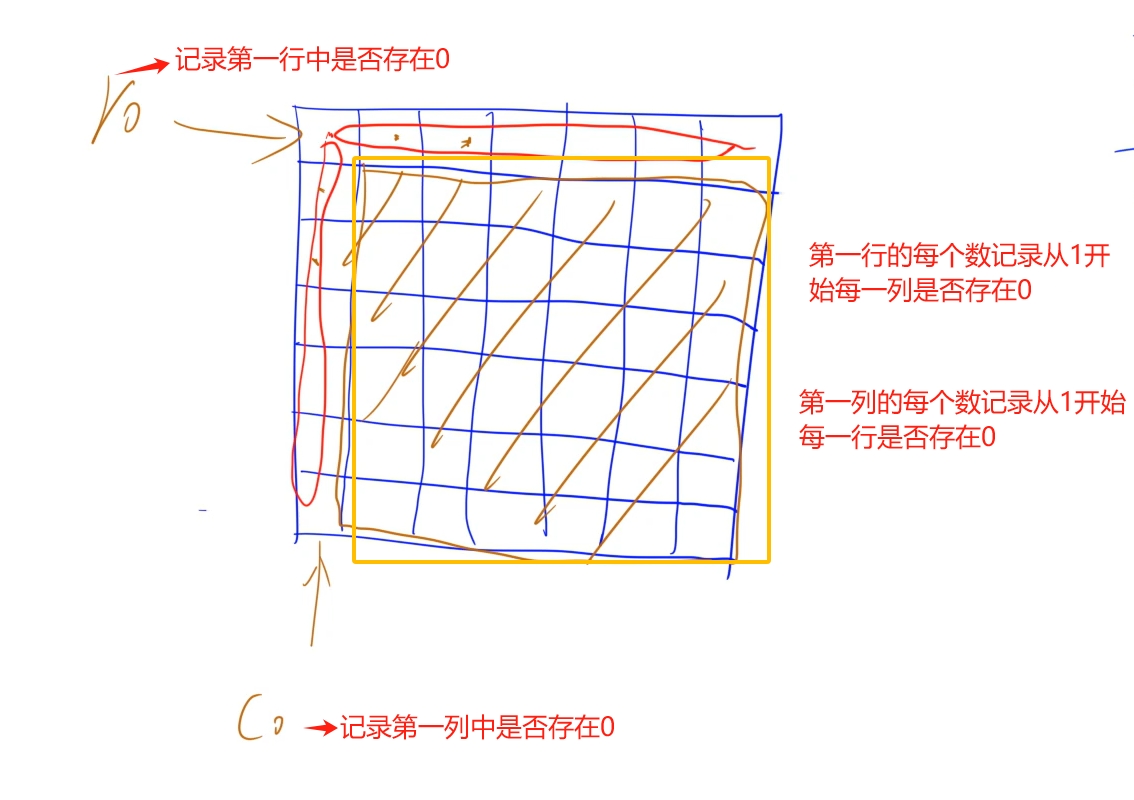
微信截图_20241121212155.png

时间复杂度：O(4 * n * n)

注释代码：

class Solution {
public:void setZeroes(vector<vector<int>>& matrix) {int n = matrix.size();  //行int m = matrix[0].size(); //列int r0 = 1, c0 = 1;//看第一行和第一列是否存在0：for(int i = 0; i < m; i++) if(!matrix[0][i]) r0 = 0;for(int i = 0; i < n; i++) if(!matrix[i][0]) c0 = 0;//用第一行和第一列存每行每列是否存在0for(int i = 1; i < m; i++){for(int j = 0; j < n; j++){if(!matrix[j][i]) matrix[0][i] = 0;}}for(int i = 1; i < n; i++){for(int j = 0; j < m; j++){if(!matrix[i][j]) matrix[i][0] = 0;}}//按第一列存储的每一行是否存在0的状态将存在的行置为全0for(int i = 1; i < n; i++){if(!matrix[i][0]){for(int j = 0; j < m; j++){matrix[i][j] = 0;}}}//按第一行存储的每一列是否存在0的状态将存在0 的列置为全0for(int i = 1; i < m; i++){if(!matrix[0][i]){for(int j= 0; j < n; j++){matrix[j][i] = 0;}}}//最后看第一行和第一列中是否存在0if(!r0) for(int i = 0; i < m; i++) matrix[0][i] = 0;if(!c0) for(int i = 0; i < n; i++) matrix[i][0] = 0;}
};

纯享版：

class Solution {
public:void setZeroes(vector<vector<int>>& matrix) {int n = matrix.size(), m = matrix[0].size();int r0 = 1, c0 = 1;for(int i = 0; i < m; i++) if(!matrix[0][i]) r0 = 0;for(int i = 0; i < n; i++) if(!matrix[i][0]) c0 = 0;for(int i = 1; i < n; i++){for(int j = 0; j < m; j++){if(!matrix[i][j]) matrix[i][0] = 0;}}for(int i = 1; i < m; i++){for(int j = 0; j < n; j++){if(!matrix[j][i]) matrix[0][i] = 0;}}for(int i = 1; i < n; i++){if(!matrix[i][0]){for(int j = 0; j < m; j++) matrix[i][j] = 0;}}for(int i = 1; i < m; i++){if(!matrix[0][i]){for(int j = 0; j < n; j++) matrix[j][i] = 0;}}if(!r0) for(int i = 0; i < m; i++) matrix[0][i] = 0;if(!c0) for(int i = 0; i < n; i++) matrix[i][0] = 0;}
};

LeetCode 74.搜索二维矩阵：

题目描述：

给你一个满足下述两条属性的 m x n 整数矩阵：

每行中的整数从左到右按非严格递增顺序排列。
每行的第一个整数大于前一行的最后一个整数。
给你一个整数 target ，如果 target 在矩阵中，返回 true ；否则，返回 false 。

示例 1：
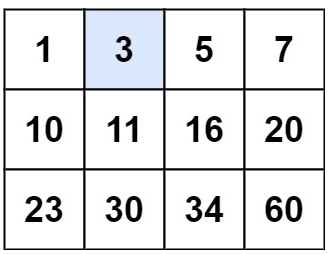
微信截图_20241121213159.png

输入：matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3
输出：true

示例 2：
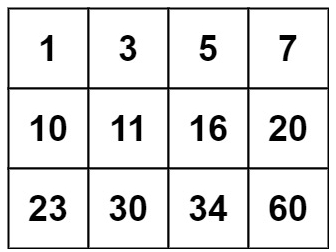
微信截图_20241121213206.png

输入：matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13
输出：false

提示：

m == matrix.length
n == matrix[i].length
1 <= m, n <= 100
-10^4 <= matrix[i][j], target <= 10^4

思路：

因为二维数组中每一行都是递增的，然后每行的第一个整数大于前一行的最后一个整数，整个二维数组每一行拼接起来也是严格递增的，那么在这个严格递增的区间中找一个target有没有熟悉的感觉！ 二分（如果没有，回去刷30道二分题）
那么如何在二维矩阵上做二分呢，这里主要就是要将原本一维上的mid 映射到二维矩阵的下标中，这里会发现：mid / m = 行 mid % m = 列
微信截图_20241121213921.png

注释代码：

class Solution {
public:bool searchMatrix(vector<vector<int>>& matrix, int target) {if(matrix.empty() || matrix[0].empty()) return false;int n = matrix.size(), m = matrix[0].size();int l = 0, r = n * m - 1;while(l < r){int mid = l + r >> 1;if(matrix[mid / m][mid % m] >= target) r = mid;else l = mid + 1;}return matrix[r / m][r % m] == target;}
};

纯享版：

class Solution {
public:bool searchMatrix(vector<vector<int>>& matrix, int target) {if(matrix.empty() || matrix[0].empty()) return false;int n = matrix.size(), m = matrix[0].size();int l = 0, r = n * m - 1;while(l < r){int mid = l + r + 1 >> 1;if(matrix[mid / m][mid % m] <= target) l = mid;else r = mid - 1;}return matrix[r / m][r % m] == target;}
};

LeetCode75.颜色分类：

题目描述：

给定一个包含红色、白色和蓝色、共 n 个元素的数组 nums ，原地对它们进行排序，使得相同颜色的元素相邻，并按照红色、白色、蓝色顺序排列。

我们使用整数 0、 1 和 2 分别表示红色、白色和蓝色。

必须在不使用库内置的 sort 函数的情况下解决这个问题。

示例 1：

输入：nums = [2,0,2,1,1,0]
输出：[0,0,1,1,2,2]

示例 2：

输入：nums = [2,0,1]
输出：[0,1,2]

提示：

n == nums.length
1 <= n <= 300
nums[i] 为 0、1 或 2

进阶：

你能想出一个仅使用常数空间的一趟扫描算法吗？

思路：

使用三指针：
0 ~ j -1: 维护0
j ~ i- 1：维护1
i ~ k：维护2
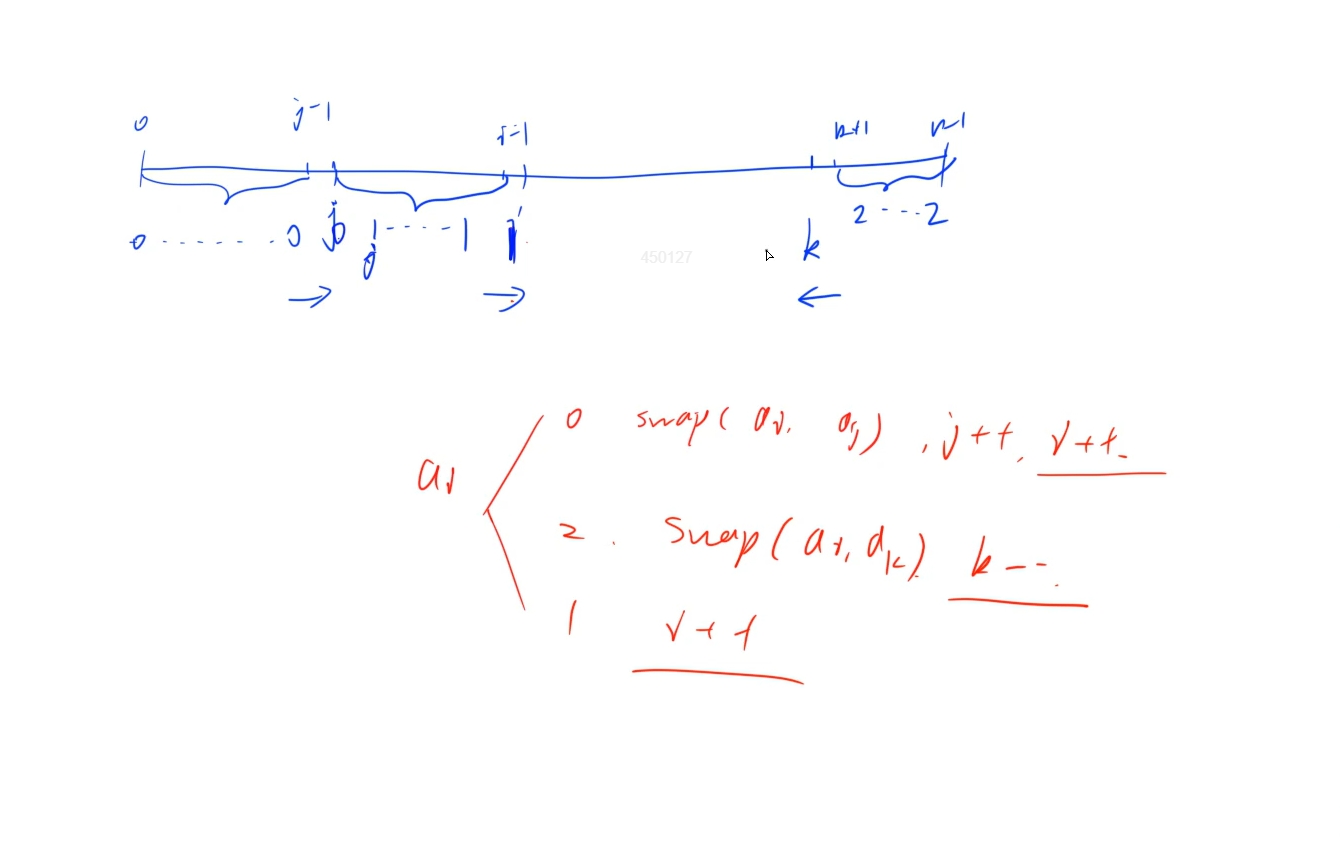
微信截图_20241121215059.png

时间复杂度：O(n)

注释代码：

class Solution {
public:void sortColors(vector<int>& nums) {for(int i = 0, j = 0, k = nums.size() -1 ; i <= k;){if(nums[i] == 0) swap(nums[i++], nums[j++]);else if(nums[i] == 2) swap(nums[i], nums[k--]);else i++;}}
};

纯享版：

class Solution {
public:void sortColors(vector<int>& nums) {for(int i = 0, j = 0, k = nums.size() -1 ; i <= k;){if(nums[i] == 0) swap(nums[i++], nums[j++]);else if(nums[i] == 2) swap(nums[i], nums[k--]);else i++;}}
};

LeetCode76.最小覆盖子串：

题目描述：

给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串，则返回空字符串 “” 。

注意：

对于 t 中重复字符，我们寻找的子字符串中该字符数量必须不少于 t 中该字符数量。
如果 s 中存在这样的子串，我们保证它是唯一的答案。

示例 1：

输入：s = “ADOBECODEBANC”, t = “ABC”
输出：“BANC”
解释：最小覆盖子串 “BANC” 包含来自字符串 t 的 ‘A’、‘B’ 和 ‘C’。

示例 2：

输入：s = “a”, t = “a”
输出：“a”
解释：整个字符串 s 是最小覆盖子串。

示例 3:

输入: s = “a”, t = “aa”
输出: “”
解释: t 中两个字符 ‘a’ 均应包含在 s 的子串中，
因此没有符合条件的子字符串，返回空字符串。

提示：

m == s.length
n == t.length
1 <= m, n <= 10^5
s 和 t 由英文字母组成

进阶：你能设计一个在 o(m+n) 时间内解决此问题的算法吗？

思路：

首先分析题意：需要在s串中找到包含t串所有字符的最小子串，那么也就是说我们需要在s串中找到包含t串所有字符的i ~ j的最小的一段，那么可以考虑使用滑动窗口来维护，那么使用滑动窗口的前提是i 和j需要具有单调性（当i往前走时j不会往后走）

单调性证明：

i ~ j 是包含t串所有字符的，那么当i往前移动时(假设i在前面) i+ 1 ~ j这一段肯定也是包含t串的所有字符的，那么j不可能往后移动，只可能往前移动或者保持在原地，于是两者都具有单调性，可以使用滑动窗口：
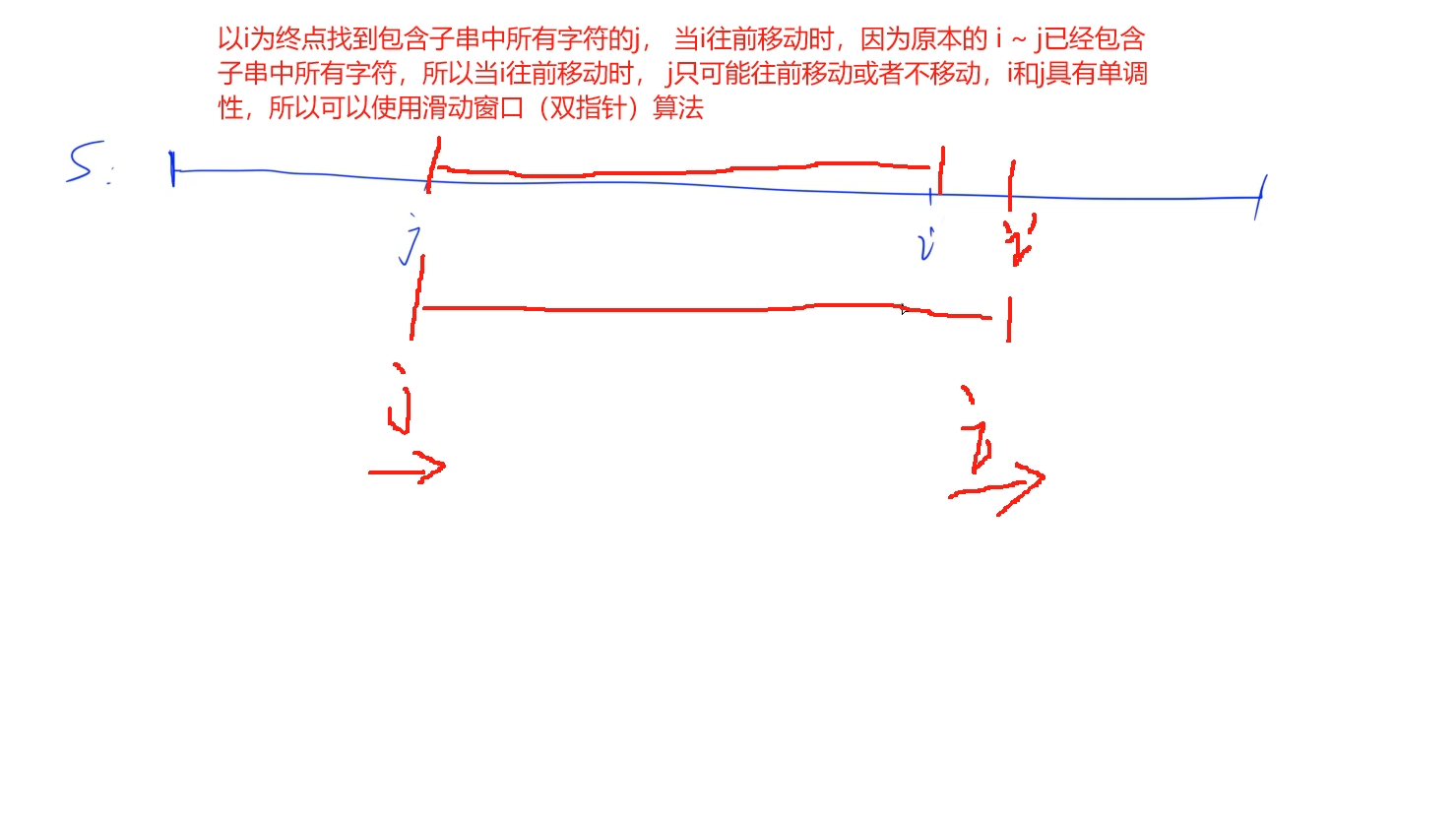
微信截图_20241122193007.png

窗口维护：

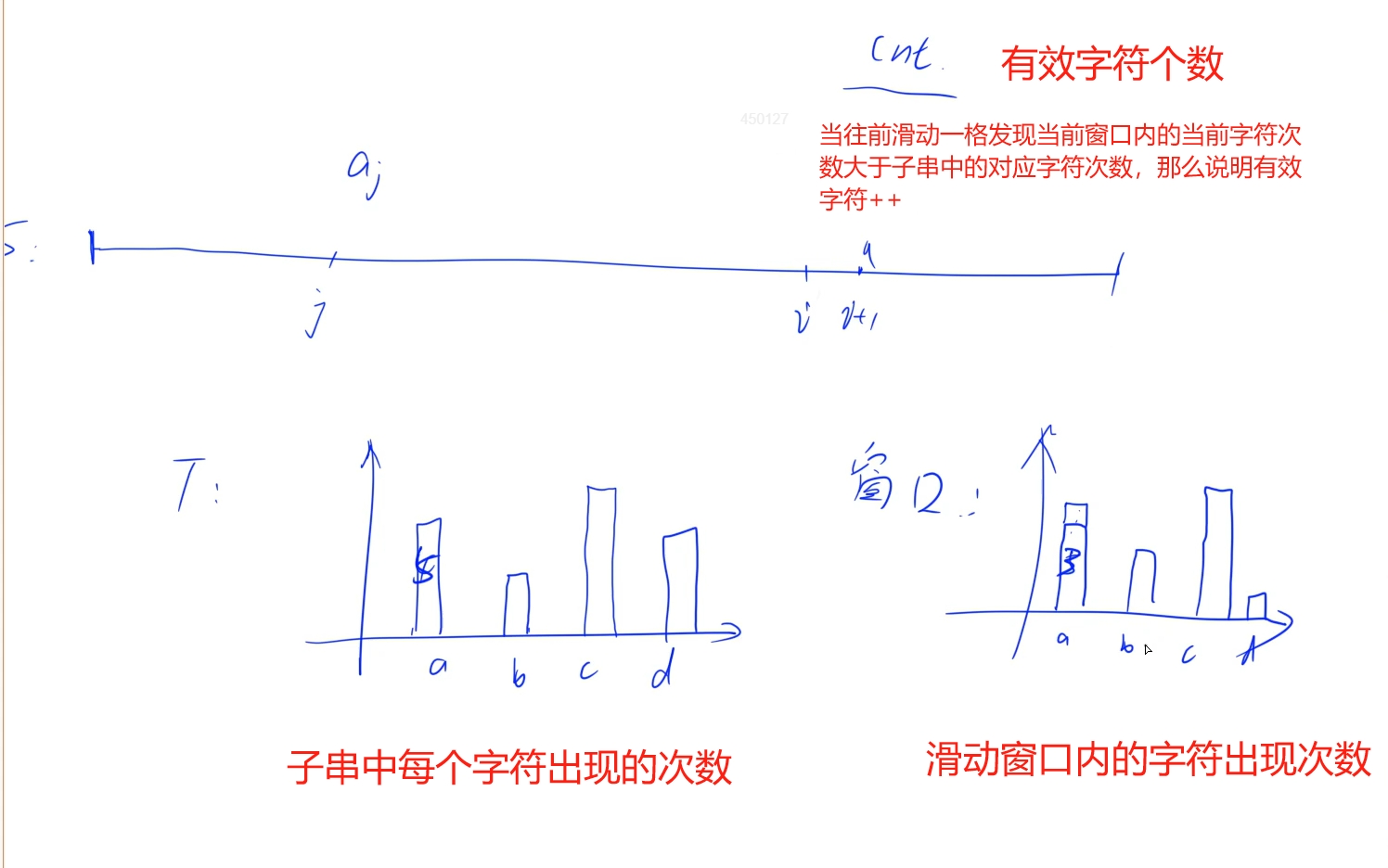
微信截图_20241122192444.png

时间复杂度：O(n)

注释代码：

class Solution {
public:string minWindow(string s, string t) {unordered_map<char, int> tot, character;for(auto c : t) tot[c]++; //子串每个字符出现的次数int cnt = 0;string res;for(int i = 0, j = 0; i < s.size(); i++){character[s[i]]++;  //当前字符出现次数+1if(character[s[i]] <= tot[s[i]]) cnt++; //如果当前字符出现是有效的，cnt有效字符个数+1//窗口后沿： 如果字符次数大于子串字符次数，那么他表示不是一个有效字符，窗口往前移动while(character[s[j]] > tot[s[j]]) character[s[j++]]--;  if(cnt == t.size()){if(res.empty() || i - j + 1 < res.size()) //当有效字符满足子串长度时，不断更新最小的窗口{res = s.substr(j, i - j + 1); //截取最小覆盖子串}}}return res;}
};

纯享版：

class Solution {
public:string minWindow(string s, string t) {unordered_map<char, int> tot, sos;for(auto c : t) tot[c]++;string res;int cnt = 0;for(int i = 0, j = 0; i < s.size(); i++){sos[s[i]]++;if(sos[s[i]] <= tot[s[i]]) cnt++;while(sos[s[j]] > tot[s[j]]) sos[s[j++]]--;if(cnt == t.size()){if(res.empty() || i - j + 1 < res.size()){res = s.substr(j, i - j + 1);}}}return res;}
};

LeetCode77.组合：

题目描述：

给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。

你可以按任何顺序返回答案。

示例 1：

输入：n = 4, k = 2
输出：
[
[2,4],
[3,4],
[2,3],
[1,2],
[1,3],
[1,4],
]

示例 2：

输入：n = 1, k = 1
输出：[[1]]

提示：

1 <= n <= 20
1 <= k <= n

思路：

dfs的适用题（组合枚举）：问题在于他需要从n个数中选k个数，而不能重复，比如： 1 2 3 跟 1 3 2
常用套路：按顺序选，将当前数的情况搜索完之后下一层dfs就应该从后一位开始搜索
微信截图_20241122200048.png

时间复杂度：

微信截图_20241122204310.png

注释代码：

class Solution {
public:vector<vector<int>> res;vector<int> path;vector<vector<int>> combine(int n, int k) {dfs(n, k, 1);return res;}//当前可以加入哪些数，加了几个， 可以从哪里开始添加void dfs(int n, int k, int start){if(!k){res.push_back(path);return;}//只能从start开始添加for(int i = start; i <= n; i++){//将当前数添加到pathpath.push_back(i);//递归下一层dfs(n, k - 1, i + 1);//恢复现场path.pop_back();}}
};

纯享版：

class Solution {
public:vector<vector<int>> res;vector<int> path;vector<vector<int>> combine(int n, int k) {dfs(n, k, 1);return res;}void dfs(int n, int k, int start){if(!k){res.push_back(path);return;}for(int i = start; i <= n; i++){path.push_back(i);dfs(n, k - 1, i + 1);path.pop_back();}}
};

LeetCode78.子集：

题目描述：

给你一个整数数组 nums ，数组中的元素互不相同。返回该数组所有可能的
子集
（幂集）。

解集不能包含重复的子集。你可以按任意顺序返回解集。

示例 1：

输入：nums = [1,2,3]
输出：[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]

示例 2：

输入：nums = [0]
输出：[[],[0]]

提示：

1 <= nums.length <= 10
-10 <= nums[i] <= 10
nums 中的所有元素互不相同

算法1：

思路：

微信截图_20241122202447.png

时间复杂度：O(2^n * n)

注释代码：

class Solution {
public:vector<vector<int>> subsets(vector<int>& nums) {vector<vector<int>> res;int n = nums.size();//枚举2^n种子集for(int i = 0; i < 1 << n; i++){vector<int> path;for(int j = 0; j < n; j++){//判断nums中的每个元素是否要选if(i >> j & 1){//当前位选path.push_back(nums[j]);}}res.push_back(path);}return res;}
};

纯享版：

class Solution {
public:vector<vector<int>> subsets(vector<int>& nums) {vector<vector<int>> res;int n = nums.size();for(int i = 0; i < 1 << n; i++){vector<int> path;for(int j = 0; j < n; j++){if(i >> j & 1){//cout<<"yes"<<endl;path.push_back(nums[j]);}}res.push_back(path);}return res;}
};

算法2：

思路：dfs 如上题所示思想

时间复杂度：O(2^n * n)

代码：

class Solution {
public:vector<vector<int>> res;vector<int> path;vector<vector<int>> subsets(vector<int>& nums) {int n = nums.size();dfs(nums,  0);return res;}void dfs(vector<int>& nums,  int start){res.push_back(path);for(int  i = start; i < nums.size(); i++){path.push_back(nums[i]);dfs(nums,  i + 1);path.pop_back();}}
};

LeetCode79.单词搜索：

题目描述：

给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中，返回 true ；否则，返回 false 。

单词必须按照字母顺序，通过相邻的单元格内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。

示例 1：

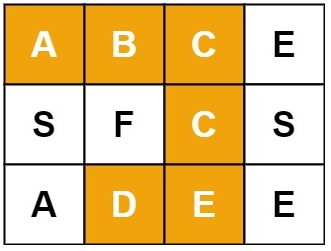
微信截图_20241123160822.png
输入：board = [[“A”,“B”,“C”,“E”],[“S”,“F”,“C”,“S”],[“A”,“D”,“E”,“E”]], word = “ABCCED”
输出：true

示例 2：
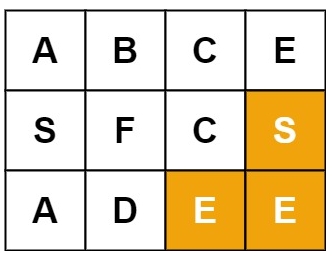
微信截图_20241123160830.png

输入：board = [[“A”,“B”,“C”,“E”],[“S”,“F”,“C”,“S”],[“A”,“D”,“E”,“E”]], word = “SEE”
输出：true

示例 3：

微信截图_20241123160837.png
输入：board = [[“A”,“B”,“C”,“E”],[“S”,“F”,“C”,“S”],[“A”,“D”,“E”,“E”]], word = “ABCB”
输出：false

提示：

m == board.length
n = board[i].length
1 <= m, n <= 6
1 <= word.length <= 15
board 和 word 仅由大小写英文字母组成

进阶：你可以使用搜索剪枝的技术来优化解决方案，使其在 board 更大的情况下可以更快解决问题？

思路：

将每个位置都看成是一个起点，找到每个位置作为起点的所有方案，
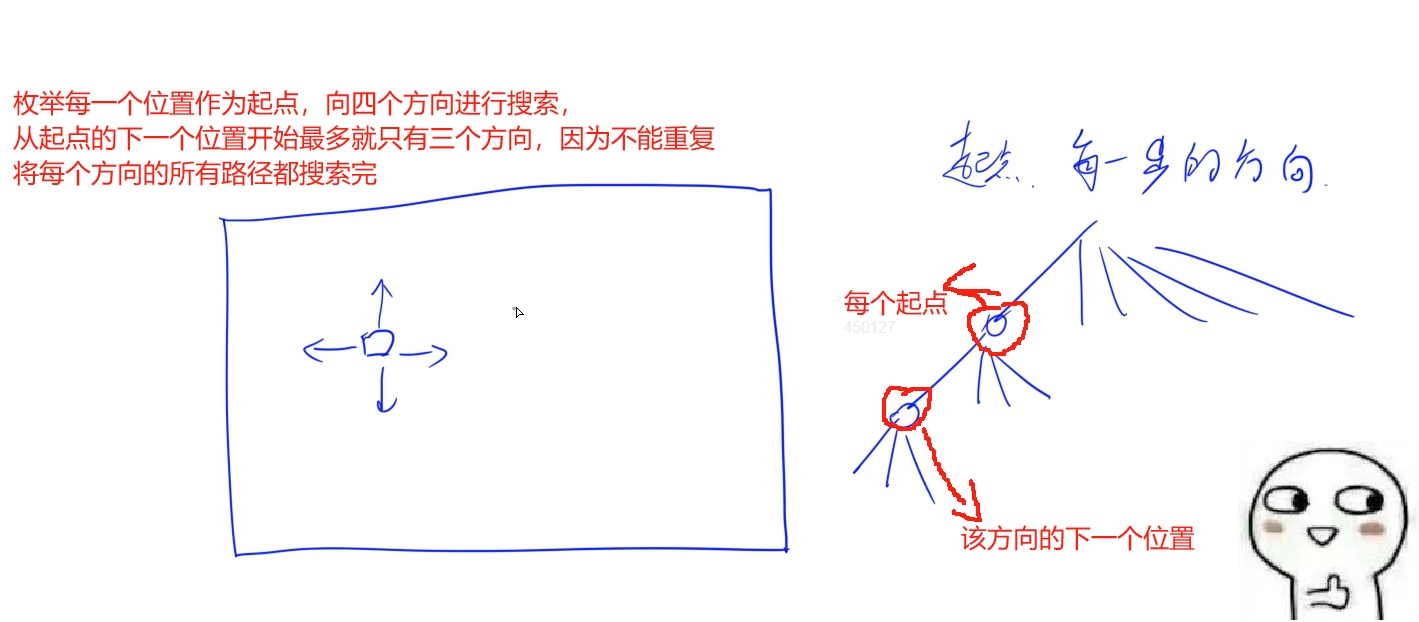
微信截图_20241123161407.png

时间复杂度：O(n * n * 3^k)

每个位置会遍历一次，对于单词的每个字符每次要向3个方向搜索： 3^k

注释代码：

class Solution {
public:bool exist(vector<vector<char>>& board, string word) {for(int i = 0; i < board.size(); i ++){for(int j = 0; j < board[0].size(); j++){//以每个位置作为起点开始往四周搜if(dfs(board, word, 0, i, j)) return true;}}return false;}//方向数组int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};bool dfs(vector<vector<char>>& board, string& word, int u, int x, int y){//如果当前搜的第u个字符不等于起点的字符那么该方向无法继续搜索if(board[x][y] != word[u]) return false;//如果搜的第u个字符已经满足需要的word长度，说明这是一种方案if(u == word.size() - 1) return true;//记录起点的字符char t = board[x][y];//将搜索过的字符进行标记board[x][y] = '.';//尝试向四个方向进行深度搜索for(int i = 0; i < 4; i++){int a = x + dx[i], b = y + dy[i];if(a < 0 || a >= board.size() || b < 0 || b >= board[0].size() || board[a][b] == '.') continue;//递归进行，直到找到当前为起点的所有方案if(dfs(board, word, u + 1, a, b)) return true;}//如果未找到方案，则需要将现场恢复board[x][y] = t;return false;}
};

纯享版：

LeetCode80.删除排序数组中的重复项Ⅱ：

题目描述：

给你一个有序数组 nums ，请你原地删除重复出现的元素，使得出现次数超过两次的元素只出现两次，返回删除后数组的新长度。

不要使用额外的数组空间，你必须在原地修改输入数组并在使用 O(1) 额外空间的条件下完成。

说明：

为什么返回数值是整数，但输出的答案是数组呢？

请注意，输入数组是以「引用」方式传递的，这意味着在函数里修改输入数组对于调用者是可见的。

你可以想象内部操作如下:

// nums 是以“引用”方式传递的。也就是说，不对实参做任何拷贝
int len = removeDuplicates(nums);

// 在函数里修改输入数组对于调用者是可见的。
// 根据你的函数返回的长度, 它会打印出数组中该长度范围内的所有元素。
for (int i = 0; i < len; i++) {
print(nums[i]);
}

示例 1：

输入：nums = [1,1,1,2,2,3]
输出：5, nums = [1,1,2,2,3]
解释：函数应返回新长度 length = 5, 并且原数组的前五个元素被修改为 1, 1, 2, 2, 3。不需要考虑数组中超出新长度后面的元素。
示例 2：

输入：nums = [0,0,1,1,1,1,2,3,3]
输出：7, nums = [0,0,1,1,2,3,3]
解释：函数应返回新长度 length = 7, 并且原数组的前七个元素被修改为 0, 0, 1, 1, 2, 3, 3。不需要考虑数组中超出新长度后面的元素。

提示：

1 <= nums.length <= 3 * 10^4
-10^4 <= nums[i] <= 10^4
nums 已按升序排列

思路：双指针

微信截图_20241123170528.png

微信截图_20241123170438.png

时间复杂度：O(n)

注释代码：

class Solution {
public:int removeDuplicates(vector<int>& nums) {int k = 0; //k作为新的下标int j = 0;for(int i = 0; i < nums.size(); i++){while(j < nums.size() && nums[i] == nums[j]) j++; nums[k++] = nums[i]; //重新替换nums，将当前位置元素添加到数组if(j - i >= 2) //之间重复超过两个 {nums[k++] = nums[i];}i = j - 1;  //跳到 j所在位置继续往后看}return k;}
};

纯享版：

LeetCode81.搜索旋转排序数组Ⅱ：

题目描述：

已知存在一个按非降序排列的整数数组 nums ，数组中的值不必互不相同。

在传递给函数之前，nums 在预先未知的某个下标 k（0 <= k < nums.length）上进行了旋转，使数组变为 [nums[k], nums[k+1], …, nums[n-1], nums[0], nums[1], …, nums[k-1]]（下标从 0 开始计数）。例如， [0,1,2,4,4,4,5,6,6,7] 在下标 5 处经旋转后可能变为 [4,5,6,6,7,0,1,2,4,4] 。

给你旋转后的数组 nums 和一个整数 target ，请你编写一个函数来判断给定的目标值是否存在于数组中。如果 nums 中存在这个目标值 target ，则返回 true ，否则返回 false 。

你必须尽可能减少整个操作步骤。

示例 1：

输入：nums = [2,5,6,0,0,1,2], target = 0
输出：true
示例 2：

输入：nums = [2,5,6,0,0,1,2], target = 3
输出：false

提示：

1 <= nums.length <= 5000
-10^4 <= nums[i] <= 10^4
题目数据保证 nums 在预先未知的某个下标上进行了旋转
-10^4 <= target <= 10^4

进阶：

此题与搜索旋转排序数组相似，但本题中的 nums 可能包含重复元素。这会影响到程序的时间复杂度吗？会有怎样的影响，为什么？

思路：

与旋转排序数组Ⅰ一致的思想，还是利用二分将区间进行分段，判断target会出现在哪段，然后在那段的范围内进行二分找到target，唯一不同的是：这里会出现重复元素，其他位置都还好，但是如果起止位置重复的话，前后区间变得无法使用是否大于nums[0]进行区分，所以我们需要先将后面重复的元素删除，重新使得区间可分
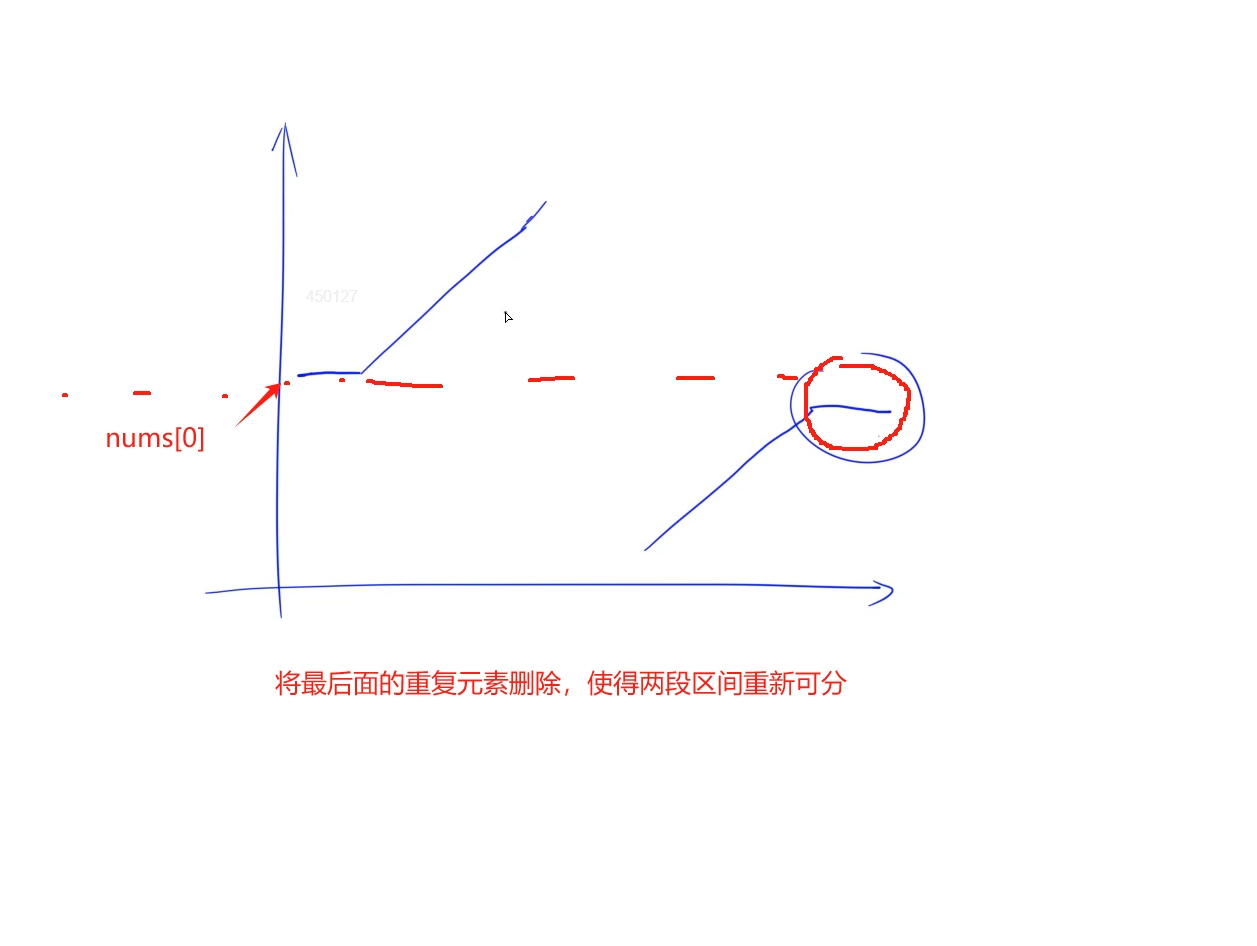
微信截图_20241124193233.png

时间复杂度：O(n)

注释代码：

class Solution {
public:bool search(vector<int>& nums, int target) {int R = nums.size() - 1;//将最后面相同的元素删去， 为了方便分段while(R >= 0 && nums[R] == nums[0]) R--;//如果R小于零， 说明全都是相等的，那么只要看最后那个是不是为target就行if(R < 0) return nums[0] == target;//将前后两段进行区分，通过nums[0]， 大于nums[0]的为前半段int l = 0, r = R;while(l < r){int mid = l + r + 1 >> 1;if(nums[mid] >= nums[0]) l = mid;else r = mid - 1;}//看在哪一段if(target >= nums[0]) r = l, l = 0;else l++, r = R;//最后在那一段中找targetwhile(l < r){int mid = l + r >> 1;if(nums[mid] >= target) r = mid;else l = mid + 1;}if(target == nums[l]) return true;else return false;}
};

纯享版：

class Solution {
public:bool search(vector<int>& nums, int target) {int R = nums.size() - 1;while(R >= 0 && nums[R] == nums[0]) R--;if(R < 0) return nums[0] == target;int l = 0, r = R;while(l < r){int mid = l + r + 1 >> 1;if(nums[mid] >= nums[0]) l = mid;else r = mid - 1;}if(target >= nums[0]) r = l, l = 0;else l++, r = R;while(l < r){int mid = l + r >> 1;if(nums[mid] >= target) r = mid;else l = mid + 1; }if(nums[r] == target) return true;else return false;}
};

LeetCode82.删除排序链表中的重复元素Ⅱ：

题目描述：

给定一个已排序的链表的头 head ，删除原始链表中所有重复数字的节点，只留下不同的数字。返回已排序的链表。

示例 1：

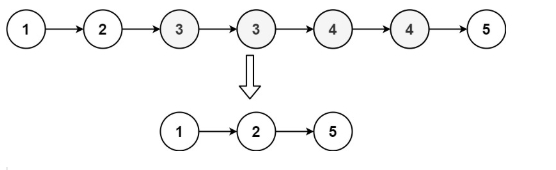
微信截图_20241124195148.png
输入：head = [1,2,3,3,4,4,5]
输出：[1,2,5]

示例 2：

微信截图_20241124195154.png
输入：head = [1,1,1,2,3]
输出：[2,3]

提示：

链表中节点数目在范围 [0, 300] 内
-100 <= Node.val <= 100
题目数据保证链表已经按升序排列

思路：

双指针思想：利用两个指针找出相同的节点值，如果相同则直接忽略它们之间的节点，如果不同则顺序衔接

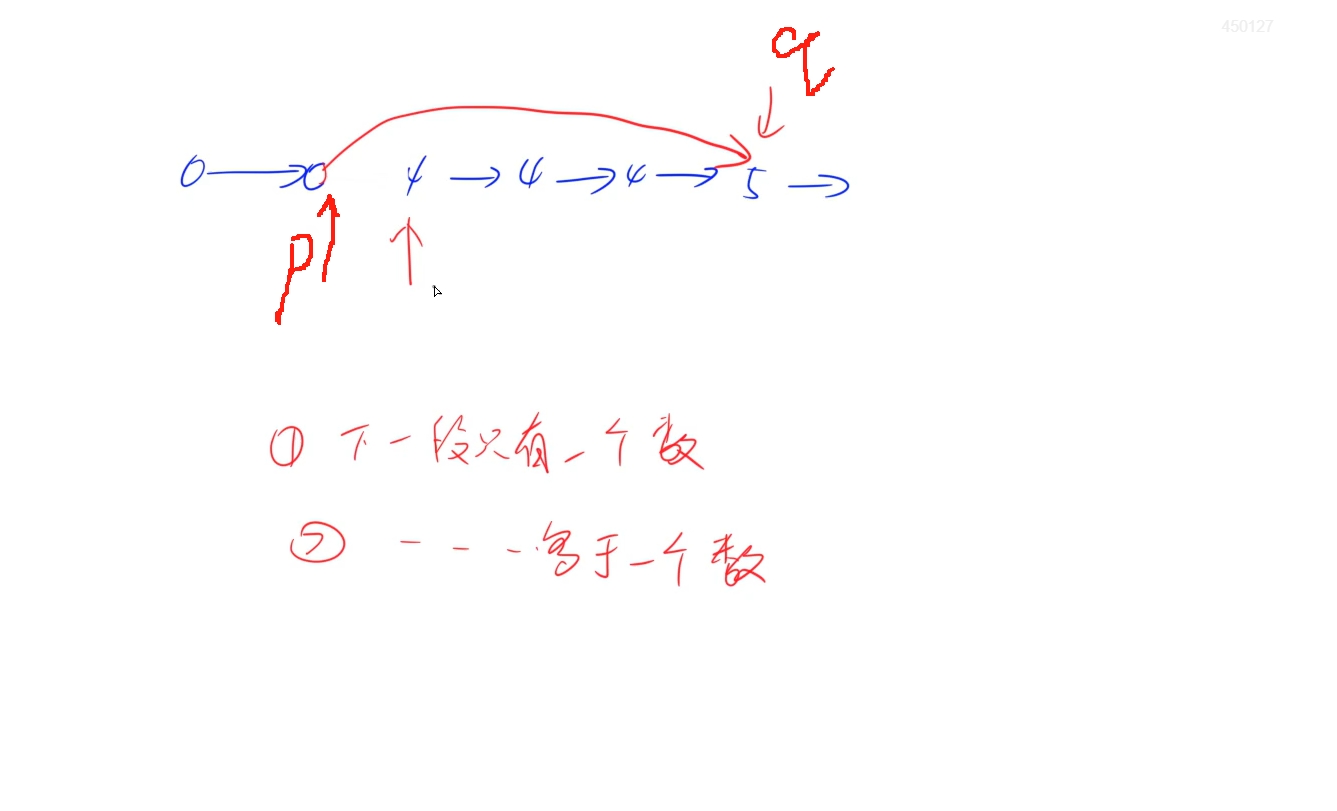
微信截图_20241124195310.png

时间复杂度：O(n)

注释代码：

/*** Definition for singly-linked list.* struct ListNode {*     int val;*     ListNode *next;*     ListNode() : val(0), next(nullptr) {}*     ListNode(int x) : val(x), next(nullptr) {}*     ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:ListNode* deleteDuplicates(ListNode* head) {auto dummy = new ListNode(-1); //虚拟头节点方便从第一个开始dummy -> next = head;auto p = dummy;while(p -> next) //有下一段时{auto q = p -> next -> next;  //找到下一段的第二个数while(q && q -> val == p -> next -> val) q = q -> next;//下段的第二个数的值跟下段第一个数的值发现两者值相同时，q往后继续if(p -> next -> next == q) p = p -> next; //如果下面的就是q说明没有相同节点值所以直接往后衔接else p -> next = q; //直接忽略相同元素}return dummy -> next;}
};

纯享版：

 */
class Solution {
public:ListNode* deleteDuplicates(ListNode* head) {auto dummy = new ListNode(-1);dummy -> next = head;auto p = dummy;while(p -> next){auto q = p -> next -> next;while(q && q -> val == p -> next -> val) q = q -> next;if(p -> next -> next == q){p = p -> next;}else p -> next = q;}return dummy -> next;}
};

LeetCode83.删除排序链表中的重复元素：

题目描述：

给定一个已排序的链表的头 head ，删除所有重复的元素，使每个元素只出现一次。返回已排序的链表。

示例 1：
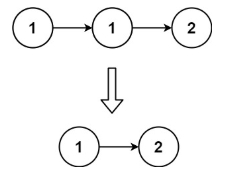
微信截图_20241124200443.png

输入：head = [1,1,2]
输出：[1,2]

示例 2：

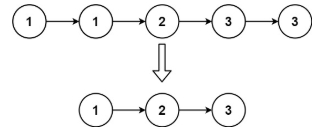
微信截图_20241124200450.png
输入：head = [1,1,2,3,3]
输出：[1,2,3]

提示：

链表中节点数目在范围 [0, 300] 内
-100 <= Node.val <= 100
题目数据保证链表已经按升序排列

思路：

由于是排序的，所以相同的值会被排序到一起，对于重复节点只保留第一个：利用cur更新链表，如果下一个节点跟当前的cur节点值不一样，就将这个节点更新到cur后面，作为第一个不同的值，相同的则忽略
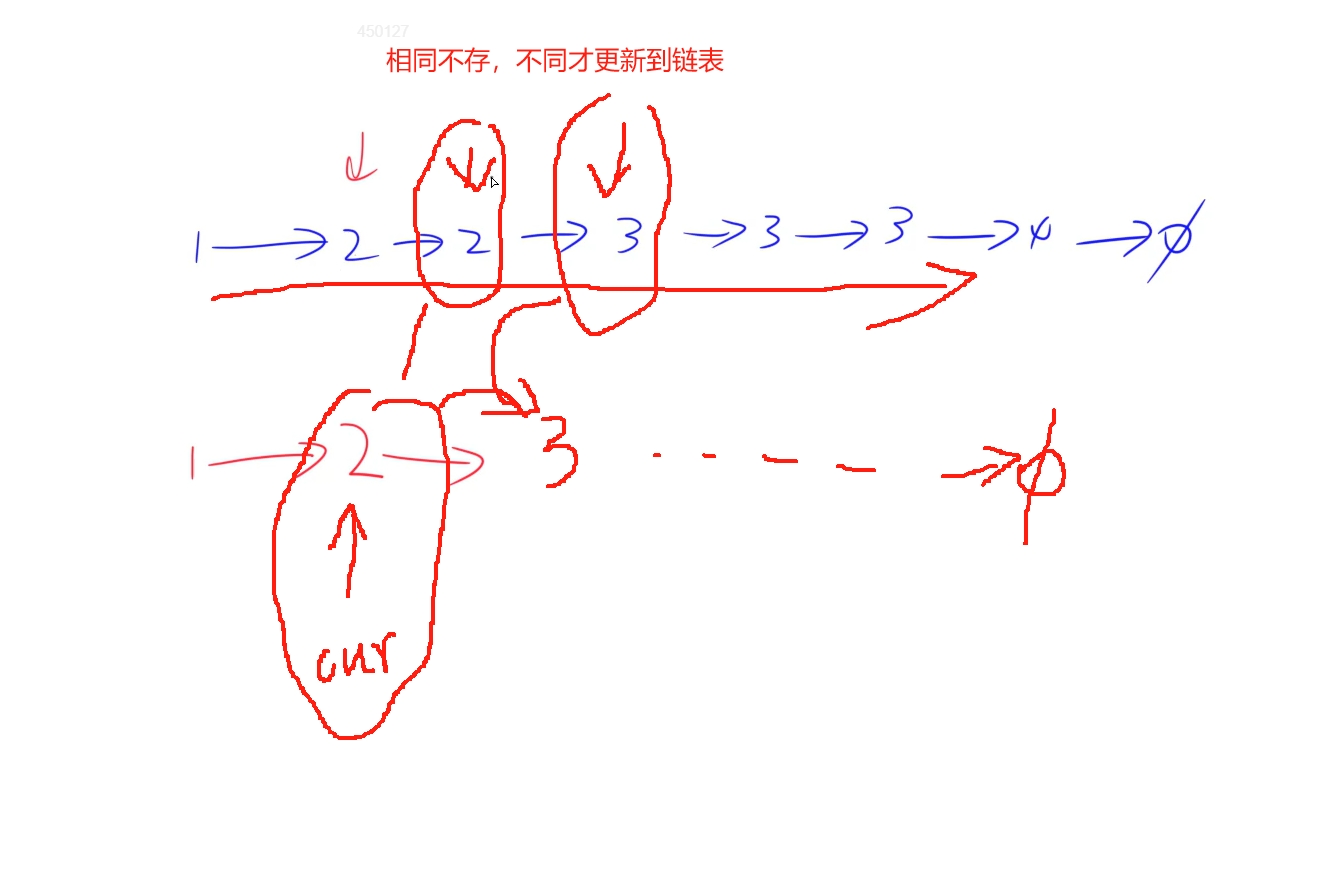
微信截图_20241124200755.png

注释代码：

/*** Definition for singly-linked list.* struct ListNode {*     int val;*     ListNode *next;*     ListNode() : val(0), next(nullptr) {}*     ListNode(int x) : val(x), next(nullptr) {}*     ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:ListNode* deleteDuplicates(ListNode* head) {if(!head) return head;auto cur = head;for(auto p = head -> next; p; p = p -> next){if(p -> val != cur -> val)  //只存第一个跟新链表前一个节点不一样的节点{cur -> next = p;cur = cur -> next;}}cur -> next = NULL;return head;}
};

纯享版：

/*** Definition for singly-linked list.* struct ListNode {*     int val;*     ListNode *next;*     ListNode() : val(0), next(nullptr) {}*     ListNode(int x) : val(x), next(nullptr) {}*     ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:ListNode* deleteDuplicates(ListNode* head) {if(!head) return head;auto cur = head;for(auto p = head -> next; p; p = p -> next){if(p -> val != cur -> val){cur -> next = p;cur = cur -> next;}}cur -> next = NULL;return head;}
};

LeetCode84.柱状图中最大的矩形：

题目描述：

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

示例 1:

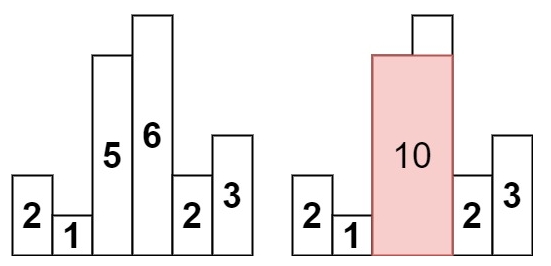
微信截图_20241125200419.png

输入：heights = [2,1,5,6,2,3]
输出：10
解释：最大的矩形为图中红色区域，面积为 10

示例 2：

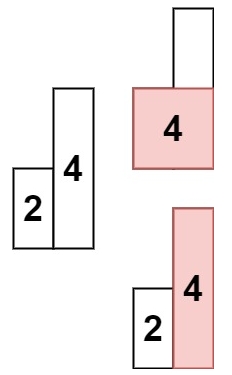
微信截图_20241125200427.png

输入： heights = [2,4]
输出： 4

提示：

1 <= heights.length <=10^5
0 <= heights[i] <= 10^4

思路：

使用单调栈思想，求出每个位置前后小于它本身数值的位置，那么以该位置为高的矩形面积就是不小于它的柱状体围成的面积：如图
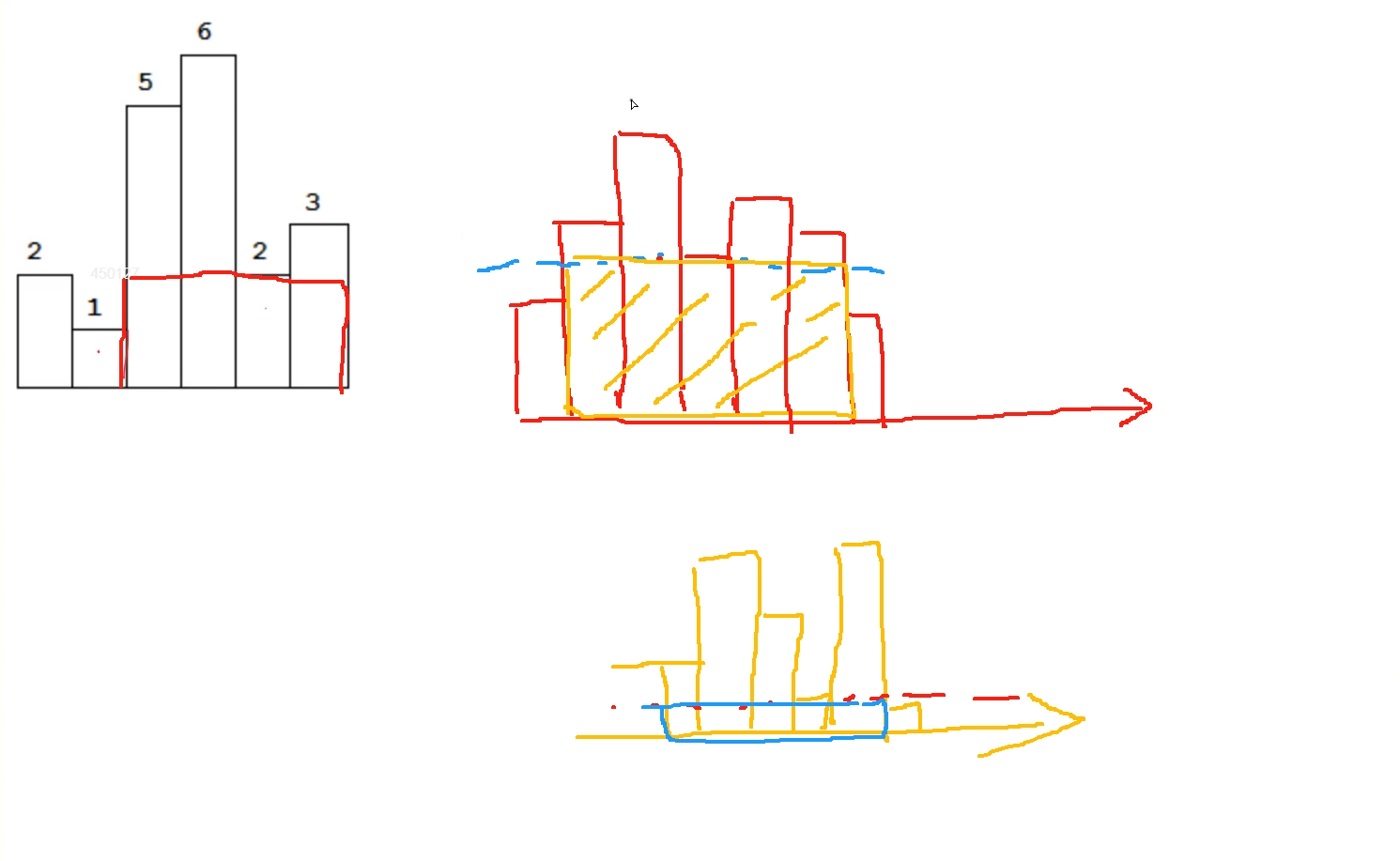
微信截图_20241125201425.png
对于每个位置求出它所能围成的最大面积，那么再对所有面积取最大值便是最大矩形

单调栈思想：
我们只需要求出当前位置左边的数第一个比他小的数，以及当前位置右边第一个比他小的数，那么在这两个数中间围成的面积，就是以当前位置的值为高的矩形所能围成的最大面积

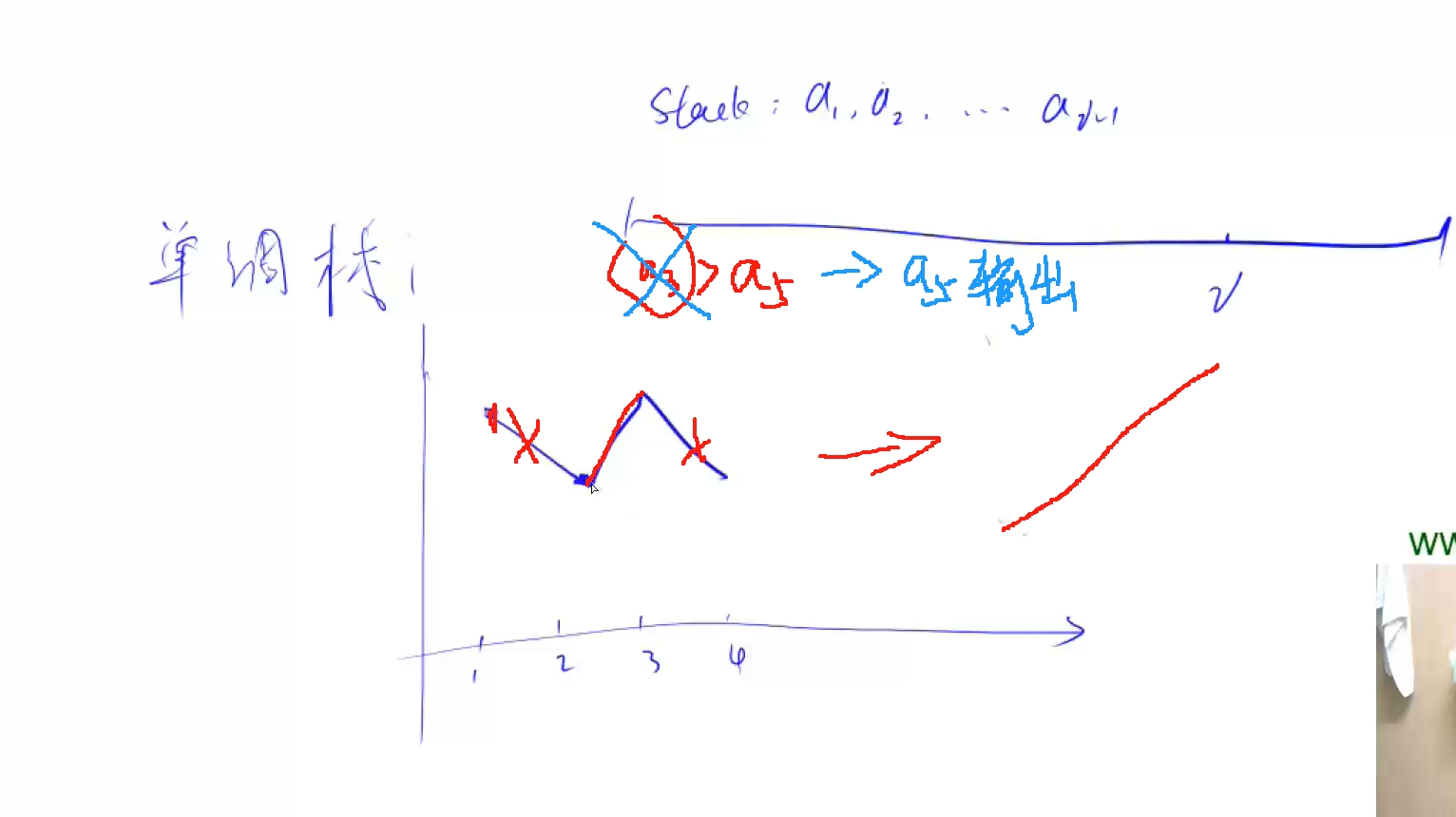
微信截图_20241125192326.png

时间复杂度：O(n)

注释代码：

class Solution {
public:int largestRectangleArea(vector<int>& h) {int n = h.size();//left 每个数左边离他最近的最小的数， right： 每个数右边离他最近的最小的数vector<int> left(n), right(n);stack<int> stk;//找到每个数左边离他最近的数for(int i = 0; i < n; i++){while(stk.size() && h[stk.top()] >= h[i]) stk.pop();if(stk.empty()) left[i] = -1;  //栈中没有元素，说明任何一个数都比当前数大，左边界可以取到最前面else left[i] = stk.top();stk.push(i);}stk = stack<int>(); //清空栈//找到每个数右边离他最近的最小数for(int i = n - 1; i >= 0; i--){while(stk.size() && h[stk.top()] >= h[i]) stk.pop();//栈中没有元素，说明任何一个数都比当前数大， 右边界可以取到右边界的下一个位置if(stk.empty()) right[i] = n;  else right[i] = stk.top();stk.push(i);}int res = 0;for(int i = 0; i < n; i++) {//cout<<right[i]<<left[i]<<' ';//求所有矩形的体积， 这里的right[i] - left[i] - 1是由于相当于 (j - 1) - (i - 1) + 1//求的是中间的矩形大小res = max(res, h[i] * (right[i] - left[i] - 1));}return res;}
};

纯享版：

class Solution {
public:int largestRectangleArea(vector<int>& h) {int n = h.size();vector<int> right(n), left(n);stack<int> stk;for(int i = 0; i < n; i++){while(stk.size() && h[stk.top()] >= h[i]) stk.pop();if(stk.empty()) left[i] = -1;else left[i] = stk.top();stk.push(i);}stk = stack<int>();for(int i = n - 1; i >= 0; i--){while(stk.size() && h[stk.top()] >= h[i]) stk.pop();if(stk.empty()) right[i] = n;else right[i] = stk.top();stk.push(i);}int ans = 0;for(int i = 0; i < n; i++) ans = max(ans, h[i] * (right[i] - left[i] - 1));return ans;}
};

LeetCode85.最大矩形：

题目描述：

给定一个仅包含 0 和 1 、大小为 rows x cols 的二维二进制矩阵，找出只包含 1 的最大矩形，并返回其面积。

示例 1：
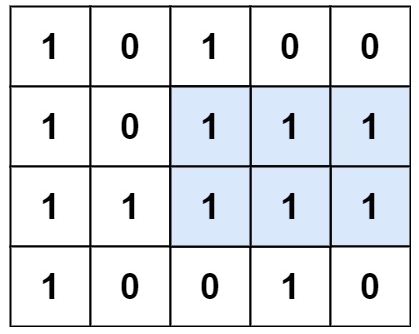
微信截图_20241125204724.png

输入：matrix = [[“1”,“0”,“1”,“0”,“0”],[“1”,“0”,“1”,“1”,“1”],[“1”,“1”,“1”,“1”,“1”],[“1”,“0”,“0”,“1”,“0”]]
输出：6
解释：最大矩形如上图所示。

示例 2：

输入：matrix = [[“0”]]
输出：0

示例 3：

输入：matrix = [[“1”]]
输出：1

提示：

rows == matrix.length
cols == matrix[0].length
1 <= row, cols <= 200
matrix[i][j] 为 ‘0’ 或 ‘1’

思路：

把它拆分为上道题的变种，就是将每一行以及它上方的由1组成的柱体看成是柱状图形式，只要求出该行每个位置上的柱状体高度就可以利用上题的代码直接求出对于该行来说，它以及它上方的柱状图形成的最大矩形

如何求每行的每个位置上的‘柱状体’高度，也就是需要求二维矩阵中每个位置上的上方连续的1的个数，我们可以使用动态规划思想，每一个位置上的状态由它上一行的同一个位置转移而来，于是h[i][j]表示(i， j)位置上连续1的个数由h[i - 1][j]加上当前位置上的1得来

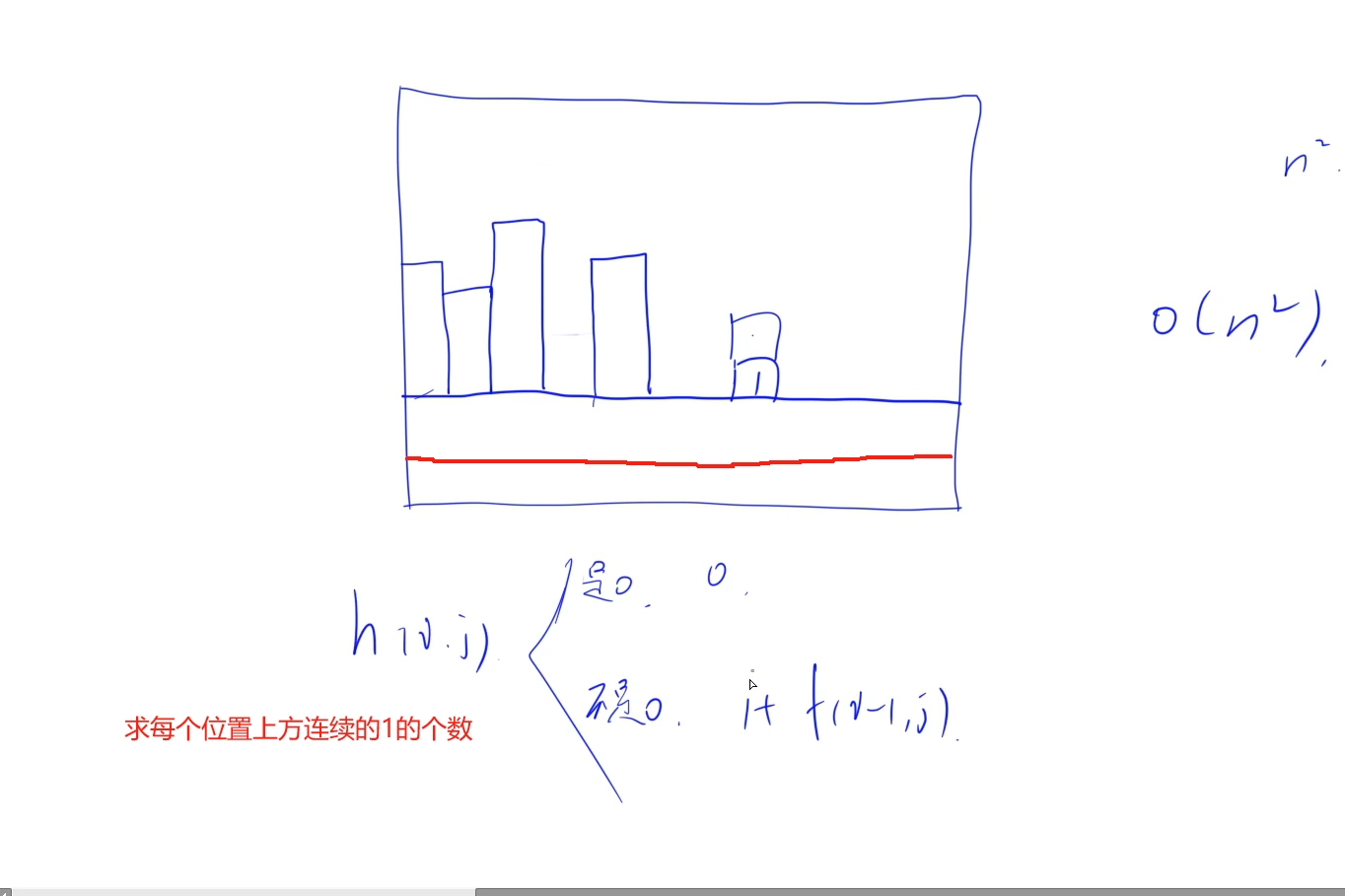
微信截图_20241125204931.png

时间复杂度：o(n * n)

注释代码：

class Solution {
public:int largestRectangleArea(vector<int>& h) {int n = h.size();vector<int> right(n), left(n);stack<int> stk;for(int i = 0; i < n; i++){while(stk.size() && h[stk.top()] >= h[i]) stk.pop();if(stk.empty()) left[i] = -1;else left[i] = stk.top();stk.push(i);}stk = stack<int>();for(int i = n - 1; i >= 0; i--){while(stk.size() && h[stk.top()] >= h[i]) stk.pop();if(stk.empty()) right[i] = n;else right[i] = stk.top();stk.push(i);}int ans = 0;for(int i = 0; i < n; i++) ans = max(ans, h[i] * (right[i] - left[i] - 1));return ans;}int maximalRectangle(vector<vector<char>>& matrix) {if(matrix.empty() || matrix[0].empty()) return 0;int n = matrix.size(), m = matrix[0].size();vector<vector<int>> h(n, vector<int>(m));  //h[i][j] 当前行的当前位置的连续1的长度for(int i = 0; i < n; i++){for(int j = 0; j < m; j++){if(matrix[i][j] == '1'){if(i) h[i][j] = 1 + h[i - 1][j]; //往上数有多少个连续的1else h[i][j] = 1;  //位于第一行，数字为1，所以它的1的高度为1}}}int res = 0;for(int i = 0; i < n; i++) res = max(res, largestRectangleArea(h[i])); //对每一行求最大矩形return res;}
};

纯享版：

class Solution {
public:int maxAera(vector<int>& h){int n = h.size();vector<int> right(n), left(n);stack<int> stk;for(int i = 0; i < n; i++){while(stk.size() && h[stk.top()] >= h[i]) stk.pop();if(stk.empty()) left[i] = -1;else left[i] = stk.top();stk.push(i);}stk = stack<int> ();for(int i = n - 1; i >= 0; i--){while(stk.size() && h[stk.top()] >= h[i]) stk.pop();if(stk.empty()) right[i] = n;else right[i] = stk.top();stk.push(i);}int res = 0; for(int i = 0; i < n; i++) res = max(res, h[i] * (right[i] - left[i] - 1));return res;}int maximalRectangle(vector<vector<char>>& matrix) {if(matrix.empty() || matrix[0].empty()) return 0;int n = matrix.size(), m = matrix[0].size();vector<vector<int>> h(n, vector<int>(m));for(int i = 0; i < n; i++){for(int j = 0; j < m; j++){if(matrix[i][j] == '1'){if(i) h[i][j] = 1 + h[i - 1][j];else h[i][j] = 1;}}}int res = 0; for(int i = 0; i < n; i++) res = max(res, maxAera(h[i]));return res;}
};

LeetCode84.分隔链表： (做链表题一定要画图！！！！)

题目描述：

给你一个链表的头节点 head 和一个特定值 x ，请你对链表进行分隔，使得所有小于 x 的节点都出现在大于或等于 x 的节点之前。

你应当保留两个分区中每个节点的初始相对位置。

示例 1：
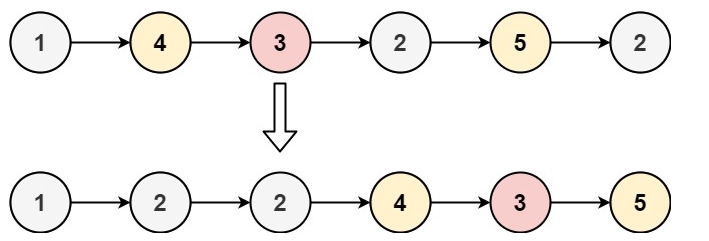
微信截图_20241125210720.png

输入：head = [1,4,3,2,5,2], x = 3
输出：[1,2,2,4,3,5]

示例 2：

输入：head = [2,1], x = 2
输出：[1,2]

提示：

链表中节点的数目在范围 [0, 200] 内
-100 <= Node.val <= 100
-200 <= x <= 200

思路：

根据题目意思要将链表以目标值分隔开，并且不打乱原本顺序，于是左右两边分别用不同链表进行存储节点值，最后合并时将左边链表的尾节点连到右边链表的头节点上：
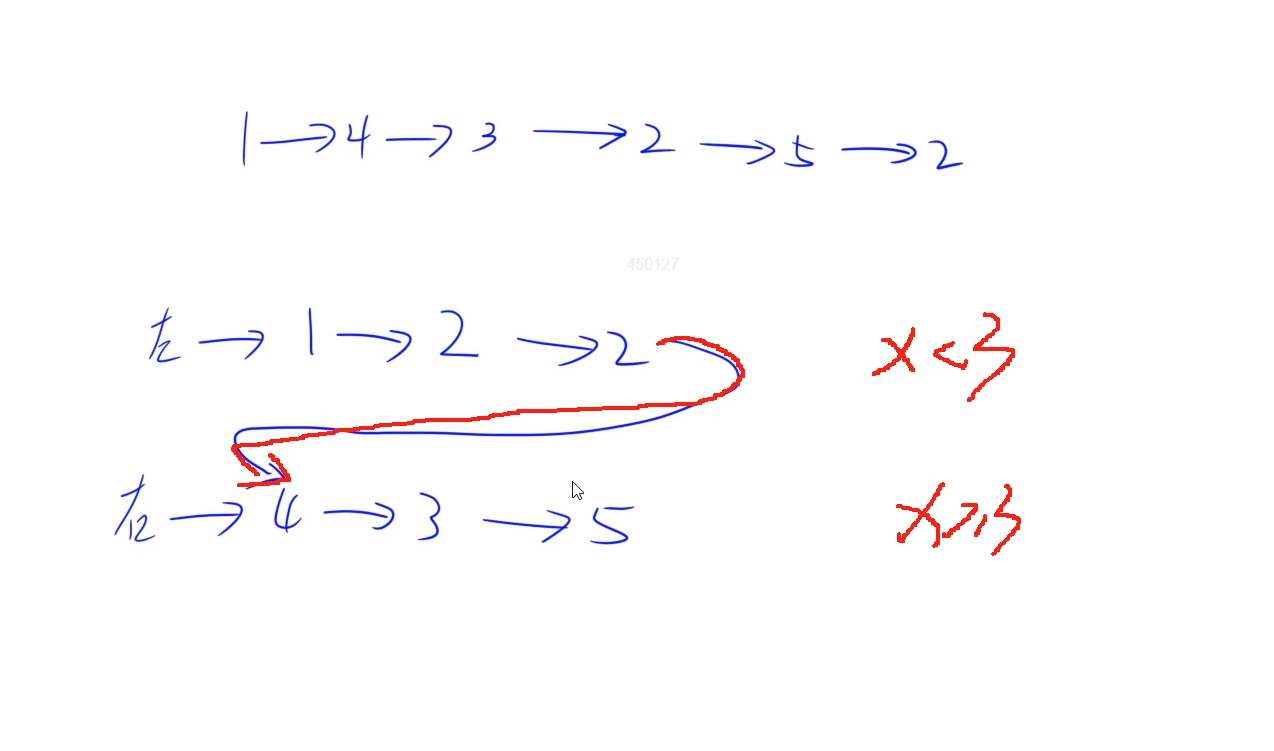
微信截图_20241125205948.png

注释代码：

/*** Definition for singly-linked list.* struct ListNode {*     int val;*     ListNode *next;*     ListNode() : val(0), next(nullptr) {}*     ListNode(int x) : val(x), next(nullptr) {}*     ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:ListNode* partition(ListNode* head, int x) {auto lh = new ListNode(-1), rh = new ListNode(-1); //左边头节点，右边头节点auto lt = lh, rt = rh; //左右的尾节点for(auto p = head; p; p = p -> next){if(p -> val < x)  //小于目标值放左边链表{lt -> next = p; //左尾指向plt = lt -> next;  //尾节点往后移动}else{rt -> next = p;rt = rt -> next;}}lt -> next = rh -> next; //左尾指向右头rt -> next = NULL; //右尾指向空return lh -> next;}
};

纯享版：

/*** Definition for singly-linked list.* struct ListNode {*     int val;*     ListNode *next;*     ListNode() : val(0), next(nullptr) {}*     ListNode(int x) : val(x), next(nullptr) {}*     ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:ListNode* partition(ListNode* head, int x) {auto lh = new ListNode(-1), rh = new ListNode(-1);auto lt = lh, rt = rh;for(auto p = head; p; p = p -> next){if(p -> val < x){lt -> next = p;lt = lt -> next;}else{rt -> next = p;rt = rt -> next;}}lt -> next = rh -> next;rt -> next = NULL;return lh -> next;}
};

LeetCode88.合并两个有序数组：

题目描述：

给你两个按非递减顺序排列的整数数组 nums1 和 nums2，另有两个整数 m 和 n ，分别表示 nums1 和 nums2 中的元素数目。

请你合并 nums2 到 nums1 中，使合并后的数组同样按非递减顺序排列。

注意：最终，合并后数组不应由函数返回，而是存储在数组 nums1 中。为了应对这种情况，nums1 的初始长度为 m + n，其中前 m 个元素表示应合并的元素，后 n 个元素为 0 ，应忽略。nums2 的长度为 n 。

示例 1：

输入：nums1 = [1,2,3,0,0,0], m = 3, nums2 = [2,5,6], n = 3
输出：[1,2,2,3,5,6]
解释：需要合并 [1,2,3] 和 [2,5,6] 。
合并结果是 [1,2,2,3,5,6] ，其中斜体加粗标注的为 nums1 中的元素。

示例 2：

输入：nums1 = [1], m = 1, nums2 = [], n = 0
输出：[1]
解释：需要合并 [1] 和 [] 。
合并结果是 [1] 。

示例 3：

输入：nums1 = [0], m = 0, nums2 = [1], n = 1
输出：[1]
解释：需要合并的数组是 [] 和 [1] 。
合并结果是 [1] 。
注意，因为 m = 0 ，所以 nums1 中没有元素。nums1 中仅存的 0 仅仅是为了确保合并结果可以顺利存放到 nums1 中。

提示：

nums1.length == m + n
nums2.length == n
0 <= m, n <= 200
1 <= m + n <= 200
-10^9 <= nums1[i], nums2[j] <= 10^9

进阶：你可以设计实现一个时间复杂度为 O(m + n) 的算法解决此问题吗？

思路：

使用归并排序思想：对比每个数组将它们中较小的那个存到数组中，但是这里有点改变，因为nums1的长度刚好为两个数组的有效元素之和nums1.length = m + n，也就是说我们需要使用nums1来存储排序之后的数组，如果从前往后做就可能覆盖nums1中的元素，所以我们需要变通，从后面往前，从后往前依次比较每个数组中的末尾，将较大的依次放到nums1的末尾

时间复制度： O(n + m)

注释代码：

class Solution {
public:void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {int k =  n + m -1;  //k为较大数的下标int  i = m - 1, j = n -1;  while(i >= 0 && j >= 0){  //从后往前存if(nums1[i] >= nums2[j]) nums1[k--] = nums1[i--];else nums1[k--] = nums2[j--];}//如果nums2还有那么将nums2剩余存起来，nums1则不用管，因为本身就存在nums1while(j >= 0) nums1[k--] = nums2[j--]; }
};

纯享版：

class Solution {
public:void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {int tail = n + m - 1;int i = m -1, j = n -1;while(i >= 0 && j >= 0){if(nums1[i] >= nums2[j]) nums1[tail--] = nums1[i--];else nums1[tail--] = nums2[j--];}while(j >= 0) nums1[tail--] = nums2[j--];}
};

LeetCode89.格雷编码：

题目描述：

n 位格雷码序列是一个由 2n 个整数组成的序列，其中：
每个整数都在范围 [0, 2n - 1] 内（含 0 和 2n - 1）
第一个整数是 0
一个整数在序列中出现不超过一次
每对相邻整数的二进制表示恰好一位不同，且
第一个和最后一个整数的二进制表示恰好一位不同
给你一个整数 n ，返回任一有效的 n 位格雷码序列。

示例 1：

输入：n = 2
输出：[0,1,3,2]
解释：
[0,1,3,2] 的二进制表示是 [00,01,11,10] 。

00 和 01 有一位不同
01 和 11 有一位不同
11 和 10 有一位不同
10 和 00 有一位不同
[0,2,3,1] 也是一个有效的格雷码序列，其二进制表示是 [00,10,11,01] 。
00 和 10 有一位不同
10 和 11 有一位不同
11 和 01 有一位不同
01 和 00 有一位不同

示例 2：

输入：n = 1
输出：[0,1]

提示：

1 <= n <= 16

思路：

找规律发现每次将前一次的结果进行对称复制然后前半部分在后面加0，后半部分加1就可以了：
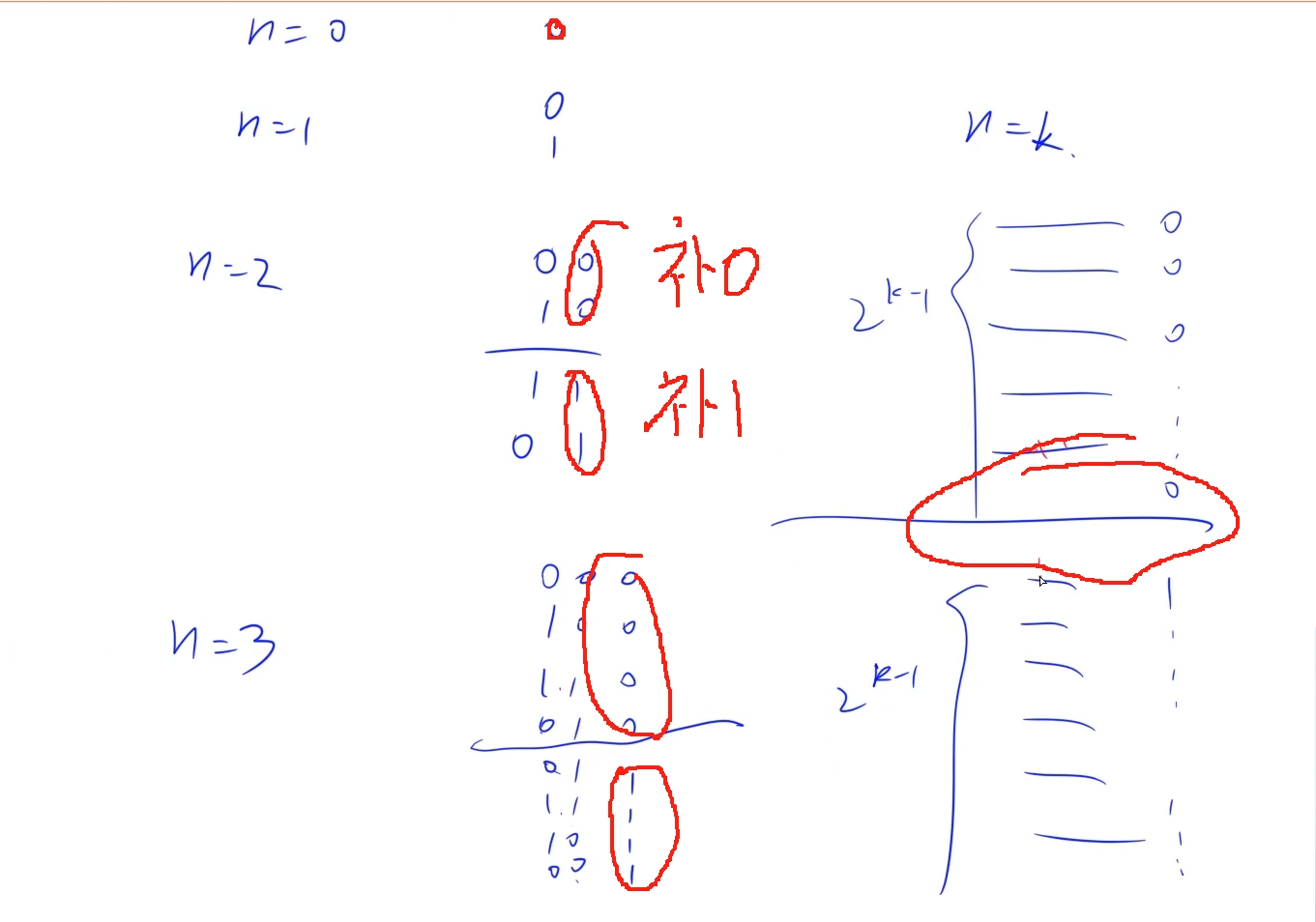
微信截图_20241126210848.png

时间复杂度： o(n)

注释代码:

class Solution {
public:vector<int> grayCode(int n) {vector<int> res(1, 0);while(n--){for(int i = res.size() - 1; i >= 0; i--){res[i] *= 2;  //前半段补零res.push_back(res[i] + 1);  //后半段在此基础上+1}}return res;}
};

纯享版：

class Solution {
public:vector<int> grayCode(int n) {vector<int> res(1,0);while(n--){for(int i = res.size() - 1; i >= 0; i--){res[i] *= 2;res.push_back(res[i] + 1);}}return res;}
};

LeetCode90.子集Ⅱ：

题目描述：

给你一个整数数组 nums ，其中可能包含重复元素，请你返回该数组所有可能的
子集
（幂集）。

解集不能包含重复的子集。返回的解集中，子集可以按任意顺序排列。

示例 1：

输入：nums = [1,2,2]
输出：[[],[1],[1,2],[1,2,2],[2],[2,2]]

示例 2：

输入：nums = [0]
输出：[[],[0]]

提示：

1 <= nums.length <= 10
-10 <= nums[i] <= 10

思路：

跟子集Ⅰ不同的是这里有相同的元素，我们需要枚举每个相同数选0个。。一个。。或者两个的情况，于是我们需要统计相同数的个数方便我们不重不漏的枚举：
微信截图_20241126212906.png

时间复杂度：

微信截图_20241126214249.png

注释代码：

class Solution {
public:vector<vector<int>> res;vector<int> path;vector<vector<int>> subsetsWithDup(vector<int>& nums) {sort(nums.begin(), nums.end());  //将所有相同数排序到一起，方便统计个数dfs(nums, 0);return res;}void dfs(vector<int>&nums, int u){if(u == nums.size()){res.push_back(path);return;}int k = u + 1;while(k < nums.size() && nums[k] == nums[u]) k++;  //统计当前相同数有多少个//当前相同数选0个 ，，1个 ，，的每种选法for(int i = 0; i <= k - u; i++){dfs(nums, k);//找完选k个数的方案path.push_back(nums[u]); //将当前数加入}for(int i = 0; i <= k - u; i++){path.pop_back(); //恢复现场}}
};

比较好理解的版本：

class Solution {
public:vector<vector<int>> res;vector<int> path;vector<vector<int>> subsetsWithDup(vector<int>& nums) {sort(nums.begin(), nums.end()); // 把所有相同的数放在一起，方便后续处理dfs(nums, 0);return res;}void dfs(vector<int>& nums, int u){res.push_back(path);for (int i = u; i < nums.size(); i ++){path.push_back(nums[i]);dfs(nums, i + 1);path.pop_back();// 只要前一个数和后一个数相同，就不再遍历这个数while (i + 1 < nums.size() && nums[i] == nums[i + 1]) ++ i;}}
};

纯享版：

class Solution {
public:vector<vector<int>> res;vector<int> path;vector<vector<int>> subsetsWithDup(vector<int>& nums) {sort(nums.begin(), nums.end());dfs(nums, 0);return res;}void dfs(vector<int>& nums, int u){if(u == nums.size()){res.push_back(path);return;}int cnt = u + 1;while(cnt < nums.size() && nums[u] == nums[cnt]) cnt++;for(int i = 0; i <= cnt - u; i++){dfs(nums, cnt);path.push_back(nums[u]);}for(int i = 0; i <= cnt - u; i++){path.pop_back();}}
};

查看全文

http://www.xdnf.cn/news/1245979.html