力扣:2246. 相邻字符不同的最长路径
给你一棵 树(即一个连通、无向、无环图),根节点是节点 0 ,这棵树由编号从 0 到 n - 1 的 n 个节点组成。用下标从 0 开始、长度为 n 的数组 parent 来表示这棵树,其中 parent[i] 是节点 i 的父节点,由于节点 0 是根节点,所以 parent[0] == -1 。
另给你一个字符串 s ,长度也是 n ,其中 s[i] 表示分配给节点 i 的字符。
请你找出路径上任意一对相邻节点都没有分配到相同字符的 最长路径 ,并返回该路径的长度。
示例 1:
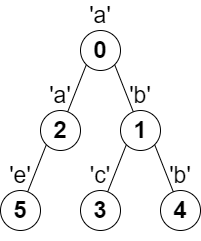
输入:parent = [-1,0,0,1,1,2], s = "abacbe" 输出:3 解释:任意一对相邻节点字符都不同的最长路径是:0 -> 1 -> 3 。该路径的长度是 3 ,所以返回 3 。 可以证明不存在满足上述条件且比 3 更长的路径。
示例 2:
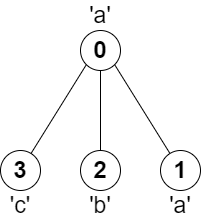
输入:parent = [-1,0,0,0], s = "aabc" 输出:3 解释:任意一对相邻节点字符都不同的最长路径是:2 -> 0 -> 3 。该路径的长度为 3 ,所以返回 3 。
提示:
n == parent.length == s.length1 <= n <= 105- 对所有
i >= 1,0 <= parent[i] <= n - 1均成立 parent[0] == -1parent表示一棵有效的树s仅由小写英文字母组成
对于这个题目我想了2种解法,文章主要讨论第二种方法。
思路1:
第一种思路也是比较无脑的解法,把树当作特殊的无向图处理,由 parent 数组关系建立邻接表,遍历所有结点,对每个结点做 dfs,递归访问相邻结点,判断相邻结点和自身的字符是否相等,相等就终止并返回,不相等就继续递归搜索。走完整棵树的所有可能,最后求出答案,但这种解法的时间复杂度显然是极大的,结果就是时间超限。
参考代码:
class Solution {
public:static const int N = 1e5 + 10;static const int INF = 0x3f3f3f3f;vector<int> a[N];//邻接表建图int ans = -INF;bool vi[N];int longestPath(vector<int>& parent, string s) {memset(vi, 0, sizeof vi);int n = s.size();for (int i = 0;i < parent.size();i++) {int u = i;int v = parent[i];if (v == -1) {continue;}a[u].push_back(v);a[v].push_back(u);}for (int i = 0;i < n;i++) {vi[i] = 1;dfs(i, 1, s);vi[i] = 0;}return ans;}bool check(int x,string s) {for (auto it : a[x]) {if (!vi[it] && s[it] != s[x]) {//相邻结点未访问且字符与该节点不同return true;}}return false;}void dfs(int x,int sum, string s) {if (!check(x, s)) {ans = max(ans, sum);return;}for (auto it : a[x]) {if (!vi[it] && s[it] != s[x]) {vi[it] = 1;//标记访问dfs(it, sum + 1, s);vi[it] = 0;}}}
};思路2:
树状dp,对于以x为根的树它的最长路径无非就是2种情况:
1、不经过x结点,整棵树的最长路径存在于x的某个子树内
2、经过x结点,整棵树的最长路径 = 从 x 结点出发到达子树的最大深度 + 第二大深度 + 1
因此我们需要每棵树的信息就是从根结点开始向下可到达的最大深度以及整棵树内部的最长路径,将这些信息在递归中返回给父节点,供父节点计算。
对于 x结点来说:如果该节点为叶子结点,他向下的最大深度和最长路径都只含自身,也就是1;如果该节点不为叶子结点,就访问其所有子节点,获取子节点(子树)的最长路径,如果子节点的字符与 x 结点字符不等,该条件下计算更新到达子节点的最大深度和第二大深度,获得这些信息后进行比较,上述的第一种情况就是获取的子树最长路径,而第二种情况也可通过计算得出。将两者的结果取最大值返回即可。
AC代码:
C++版本:
class Solution {
public:typedef struct {int w;//以该节点为根的最长路径长度int len;//该结点向下的最大深度}Node;static const int N = 1e5 + 10;vector<int> a[N];int longestPath(vector<int>& parent, string s) {for (int i = 0;i < parent.size();i++) {int ch = i;int fa = parent[i];if (fa == -1) {continue;}a[fa].push_back(ch);}return fun(0, s).w;}Node fun(int x, string& s) {Node t;t.w = 1;t.len = 1;int dep1 = 0;int dep2 = 0;for (auto it : a[x]) {Node k = fun(it, s);if (s[x] != s[it]) {//该节点字符与子结点字符不等t.len = max(t.len, k.len + 1);//获取子树的最大深度if (dep1 <= k.len) {//获取子节点的最大和第二大深度dep2 = dep1;dep1 = k.len;}else if (dep2 < k.len) {dep2 = k.len;}}t.w = max(t.w, k.w);//获取子节点可分配的最长路径长度}t.w = max(t.w, dep1 + dep2 + 1);return t;}
};java版本:
import java.util.ArrayList;class Solution {class Node{int w;int len;public Node() {}public Node(int w, int len) {this.w = w;this.len = len;}}public final int N=100010;public ArrayList<Integer>[] a=new ArrayList[N];public int longestPath(int[] parent, String s) {int n=parent.length;for (int i = 0; i < n; i++) {a[i]=new ArrayList<>();}for (int i = 0; i < parent.length; i++) {int ch=i;int fa=parent[i];if(fa==-1){continue;}a[fa].add(ch);}return fun(0,s).w;}public Node fun(int x,String s){Node t=new Node(1,1);if(a[x].isEmpty()){return t;}int dep1=0;int dep2=0;for (int i = 0; i < a[x].size(); i++) {Node k=fun(a[x].get(i),s);if(s.charAt(x)!=s.charAt(a[x].get(i))) {t.len = Math.max(t.len, k.len + 1);if (dep1 <= k.len) {dep2 = dep1;dep1 = k.len;} else if (dep2 < k.len) {dep2 = k.len;}}t.w=Math.max(t.w,k.w);}t.w=Math.max(t.w,dep1+dep2+1);return t;}
}