并查集介绍及典型应用和编程题

视频学习:

链接1: 程序员卡尔 图论：并查集理论基础！
链接2: 并查集(Union Find)
链接3: 并查集 - 基本操作, 路径压缩, 按秩合并)

并查集介绍

并查集（Union-Find）是一种用于处理不相交集合的合并与查询问题的树型数据结构，特别适合解决动态连通性问题。它支持两种基本操作：合并（Union） 和 查找（Find），因此得名。
并查集基本操作：
1.查找find(x) 查找x的根节点。 递归查找，路径压缩。
python中 self.parent[x] = self.find(self.parent[x]) 是赋值语句，没有返回值。
2.union(x,y) 合并两个集合。 按秩合并。

class UnionFind:def __init__(self, size):"""初始化并查集，每个元素指向自己，秩为0"""self.parent = list(range(size))self.rank = [0] * sizeself.count = size  # 连通分量计数def find(self, x):"""查找根节点（路径压缩优化）"""if self.parent[x] == xreturn xelse:# 递归查找并压缩路径self.parent[x] = self.find(self.parent[x])return self.parent[x]def union(self, x, y):"""合并两个集合（按秩合并优化）"""rootX = self.find(x)rootY = self.find(y)# 已在同一集合中if rootX == rootY:return False# 按秩合并：小树挂到大树下if self.rank[rootX] < self.rank[rootY]:self.parent[rootX] = rootYelif self.rank[rootX] > self.rank[rootY]:self.parent[rootY] = rootXelse:# 秩相同则任意挂接，并增加秩self.parent[rootY] = rootXself.rank[rootX] += 1self.count -= 1  # 连通分量减少return Truedef connected(self, x, y):"""检查两个元素是否连通"""return self.find(x) == self.find(y)def components(self):"""返回当前连通分量数量"""return self.count

使用示例

# 创建并查集（10个元素）
uf = UnionFind(10)# 初始状态：10个独立集合
print("初始连通分量:", uf.components())  # 输出: 10# 建立连接关系
uf.union(1, 2)
uf.union(2, 5)
uf.union(5, 6)
uf.union(3, 8)# 检查连通性
print("1和6是否连通:", uf.connected(1, 6))  # 输出: True
print("3和8是否连通:", uf.connected(3, 8))  # 输出: True
print("1和8是否连通:", uf.connected(1, 8))  # 输出: False# 合并两个连通分量
uf.union(6, 8)
print("合并后1和8是否连通:", uf.connected(1, 8))  # 输出: True
print("当前连通分量:", uf.components())  # 输出: 6

#并查集在连通性问题中的应用

并查集（Union-Find）数据结构是解决连通性问题的利器，特别适合处理动态连接关系。下面我将通过几个典型应用场景展示如何使用Python实现并查集解决实际问题。

1.计算图的连通分量数量

def count_components(n, edges):uf = UnionFind(n)for a, b in edges:uf.union(a, b)return uf.components()# 示例：4个节点，2条边
edges = [[0, 1], [2, 3]]
print("连通分量:", count_components(4, edges))  # 输出: 2

2. 网络连接检测

检测计算机网络中设备之间的连通性：

class Network:def __init__(self, n):"""初始化网络，n个设备"""self.uf = UnionFind(n)def connect(self, device1, device2):"""连接两个设备"""self.uf.union(device1, device2)print(f"已连接设备 {device1} 和 {device2}")def is_connected(self, device1, device2):"""检查两个设备是否连通"""connected = self.uf.connected(device1, device2)print(f"设备 {device1} 和 {device2} {'连通' if connected else '不连通'}")return connecteddef network_components(self):"""返回网络中的连通分量数量"""count = self.uf.components()print(f"当前网络有 {count} 个独立子网")return count# 使用示例
net = Network(6)  # 创建6个设备的网络
net.network_components()  # 输出: 当前网络有 6 个独立子网net.connect(0, 1)
net.connect(1, 2)
net.connect(3, 4)net.is_connected(0, 2)  # 输出: 设备 0 和 2 连通
net.is_connected(0, 3)  # 输出: 设备 0 和 3 不连通
net.network_components()  # 输出: 当前网络有 3 个独立子网net.connect(2, 4)  # 连接两个子网
net.is_connected(0, 4)  # 输出: 设备 0 和 4 连通
net.network_components()  # 输出: 当前网络有 2 个独立子网

3. 朋友圈关系分析

分析社交网络中的朋友圈关系：

class SocialNetwork:def __init__(self, people):"""初始化社交网络，people是人员列表"""self.people = peopleself.id_map = {name: i for i, name in enumerate(people)}self.uf = UnionFind(len(people))def add_friendship(self, person1, person2):"""添加朋友关系"""id1 = self.id_map[person1]id2 = self.id_map[person2]self.uf.union(id1, id2)print(f"{person1} 和 {person2} 成为朋友")def in_same_circle(self, person1, person2):"""检查两人是否在同一个朋友圈"""id1 = self.id_map[person1]id2 = self.id_map[person2]same_circle = self.uf.connected(id1, id2)print(f"{person1} 和 {person2} {'在' if same_circle else '不在'}同一个朋友圈")return same_circledef friend_circles(self):"""返回所有朋友圈"""circles = {}for i, person in enumerate(self.people):root = self.uf.find(i)if root not in circles:circles[root] = []circles[root].append(person)print("\n当前朋友圈:")for circle in circles.values():print(f" - {', '.join(circle)}")return list(circles.values())# 使用示例
people = ["Alice", "Bob", "Charlie", "David", "Eve", "Frank"]
social_net = SocialNetwork(people)social_net.add_friendship("Alice", "Bob")
social_net.add_friendship("Bob", "Charlie")
social_net.add_friendship("David", "Eve")social_net.in_same_circle("Alice", "Charlie")  # 在同一个朋友圈
social_net.in_same_circle("Alice", "David")    # 不在同一个朋友圈social_net.add_friendship("Charlie", "Eve")  # 合并两个朋友圈
social_net.friend_circles()

4. Kruskal最小生成树算法

在图论中使用并查集实现Kruskal算法：

def kruskal_mst(nodes, edges):"""使用Kruskal算法计算最小生成树:param nodes: 节点列表:param edges: 边列表，格式为[(node1, node2, weight), ...]:return: 最小生成树的边列表"""# 创建并查集node_ids = {node: i for i, node in enumerate(nodes)}uf = UnionFind(len(nodes))# 按权重对边进行排序edges.sort(key=lambda x: x[2])mst = []  # 最小生成树total_weight = 0for edge in edges:node1, node2, weight = edgeid1, id2 = node_ids[node1], node_ids[node2]# 如果两个节点不在同一个集合中，则不会形成环if not uf.connected(id1, id2):uf.union(id1, id2)mst.append(edge)total_weight += weight# 如果已经连接所有节点，提前结束if len(mst) == len(nodes) - 1:break# 检查是否形成完整生成树if len(mst) < len(nodes) - 1:print("图不连通，无法形成完整生成树")return Noneprint(f"最小生成树权重: {total_weight}")print("最小生成树包含边:")for edge in mst:print(f"{edge[0]} -- {edge[1]} (权重: {edge[2]})")return mst# 使用示例
nodes = ['A', 'B', 'C', 'D', 'E']
edges = [('A', 'B', 4),('A', 'C', 2),('B', 'C', 1),('B', 'D', 5),('C', 'D', 8),('C', 'E', 10),('D', 'E', 2)
]mst = kruskal_mst(nodes, edges)

4. 岛屿数量问题

解决LeetCode上的岛屿数量问题：

def num_islands(grid):"""计算二维网格中的岛屿数量:param grid: 二维网格，'1'表示陆地，'0'表示水:return: 岛屿数量"""if not grid:return 0rows, cols = len(grid), len(grid[0])uf = UnionFind(rows * cols)# 记录陆地数量land_count = 0# 遍历网格for i in range(rows):for j in range(cols):if grid[i][j] == '1':land_count += 1index = i * cols + j# 检查上方是否是陆地if i > 0 and grid[i-1][j] == '1':up_index = (i-1) * cols + jif uf.union(index, up_index):land_count -= 1# 检查左方是否是陆地if j > 0 and grid[i][j-1] == '1':left_index = i * cols + (j-1)if uf.union(index, left_index):land_count -= 1return land_count# 使用示例
grid = [['1', '1', '0', '0', '0'],['1', '1', '0', '0', '0'],['0', '0', '1', '0', '0'],['0', '0', '0', '1', '1']
]print("岛屿数量:", num_islands(grid))  # 输出: 3

OD题目

【华为OD机试真题】436、5G网络建设 | 机试真题+思路参考+代码解析（最新CD卷抽中）

题目描述：
现需要在某城市进行5G网络建设，已经选取N个地点设置5G基站，编号固定为1到N，接下来需要各个基站之间使用光纤进行连接以确保基站能互联互通，不同基站之间架设光纤的成本各不相同，且有些节点之间可能存在光纤相连，请你设计算法，计算出能联通这些基站的最小成本是多少。
注意：基站的联通具有传递性，如基站A与基站B架设了光纤，基站B与基站C也架设了光纤，则基站A与基站C视为可以互相联通。
输入输出：
输入
第一行输入表示基站的个数N，其中0<N<=20
第二行输入表示具备光纤直连条件的基站对的数目M，其中0<M<=N*(N-1)/2
第三行开始连续输入M行数据，格式为X Y Z P，其中X、Y表示基站的编号，0<X<=N, 0<Y<=N且X不等于Y，Z表示在X Y之间架设光纤的成本，其中0<Z<100，P表示是否已存在光纤连接，0表示未连接，1表示已连接
输出
如果给定条件，可以建设成功互联互通的5G网络，则输出最小的建设成本；
如果给定条件，无法建设成功互联互通的5G网络，则输出-1

输入
3
3
1 2 3 0
1 3 1 0
2 3 5 0输出
4

# 并查集数据结构
class UnionFind:def __init__(self, n):# 初始化每个节点的父节点为其自身self.parent = [i for i in range(n)]def find(self, x):# 查找节点x的根节点if self.parent[x] != x:self.parent[x] = self.find(self.parent[x])return self.parent[x]def union(self, x, y):# 合并节点x和y所在的集合root_x = self.find(x)root_y = self.find(y)if root_x != root_y:self.parent[root_y] = root_xreturn Truereturn False# 计算连接所有站点的最小成本
def min_cost_to_connect_stations(N, connections):uf = UnionFind(N)total_cost = 0# 首先处理已经存在的连接，不增加额外成本for x, y, cost, connected in connections:if connected == 1:uf.union(x - 1, y - 1)  # 减1是因为并查集中节点索引是从0开始的# 对所有未连接的边按成本从低到高排序remaining_connections = [c for c in connections if c[3] == 0]remaining_connections.sort(key=lambda x: x[2])# 使用克鲁斯卡尔算法逐条检查未连接的边for x, y, cost, connected in remaining_connections:# 如果添加这条边不会造成循环，则添加到MST中if uf.union(x - 1, y - 1):total_cost += cost# 检查是否所有节点都已经连接在同一棵树上root = uf.find(0)for i in range(1, N):if uf.find(i) != root:return -1  # 如果有节点未连接，返回-1return total_cost# 读取输入数据
N = int(input())
M = int(input())
connections = []
for _ in range(M):x, y, z, p = map(int, input().split())connections.append((x, y, z, p))# 计算最小成本并输出
min_cost = min_cost_to_connect_stations(N, connections)
print(min_cost)

【华为OD机试真题】287、图像物体的边界 | 机试真题+思路参考+代码分析

项目描述：
给定一个二维数组M行N列，二维数组里的数字代表图片的像素，为了简化问题，仅包含像素1和5两种像素，每种像素代表一个物体，2个物体相邻的格子为边界，求像素1代表的物体的边界的个数。
像素1代表的物体的边界指与像素5相邻的像素1的格子，边界相邻的属于同一个边界，相邻需要考虑8个方向（上，下，左，右，左上，左下，右上，右下）。
其他约束：
地图规格约束为：
0 < M = 100
0 < N = 100
1.如下图，与像素5的格子相邻的像素1的格子(0,0),(0,1),(0,2),(1,0),(1,2),(2,0),(2,1),(2,2),(4,4),(4,5),(5,4)为边界，另(0,0),(0,1),(0,2),(1,0),(1,2),(2,0),(2,1),(2,2)相邻，为1个边界；(4,4),(4,5),(5,4)相邻，为1个边界，所以下图边界个数为2。

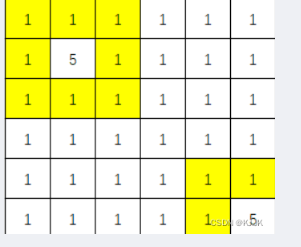
输入
6 6
1 1 1 1 1 1
1 5 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 5输出
2

# 并查集数据结构
class UnionFind:def __init__(self, n):# 初始化每个节点的父节点为其自身self.parent = [i for i in range(n)]def find(self, x):# 查找节点x的根节点if self.parent[x] != x:self.parent[x] = self.find(self.parent[x])return self.parent[x]def union(self, x, y):# 合并节点x和y所在的集合root_x = self.find(x)root_y = self.find(y)if root_x != root_y:self.parent[root_y] = root_xreturn Truereturn False# 计算连接所有站点的最小成本
def min_cost_to_connect_stations(N, connections):uf = UnionFind(N)total_cost = 0# 首先处理已经存在的连接，不增加额外成本for x, y, cost, connected in connections:if connected == 1:uf.union(x - 1, y - 1)  # 减1是因为并查集中节点索引是从0开始的# 对所有未连接的边按成本从低到高排序remaining_connections = [c for c in connections if c[3] == 0]remaining_connections.sort(key=lambda x: x[2])# 使用克鲁斯卡尔算法逐条检查未连接的边for x, y, cost, connected in remaining_connections:# 如果添加这条边不会造成循环，则添加到MST中if uf.union(x - 1, y - 1):total_cost += cost# 检查是否所有节点都已经连接在同一棵树上root = uf.find(0)for i in range(1, N):if uf.find(i) != root:return -1  # 如果有节点未连接，返回-1return total_cost# 读取输入数据
N = int(input())
M = int(input())
connections = []
for _ in range(M):x, y, z, p = map(int, input().split())connections.append((x, y, z, p))# 计算最小成本并输出
min_cost = min_cost_to_connect_stations(N, connections)
print(min_cost)

并查集的优势

1. 高效处理动态连通性问题：在添加新连接时能够快速更新连通状态
2. 时间复杂度优异：路径压缩和按秩合并使操作接近常数时间
3. 空间复杂度低：仅需O(n)额外空间
4. 实现简洁：核心代码只需几十行，易于理解和实现

这些示例展示了并查集在各种连通性问题中的强大应用能力，从网络连接到社交关系分析，再到图论算法和二维网格问题。通过并查集，我们可以高效解决许多看似复杂的连通性问题。