计算机算术4-整形乘法

1. 算法简介

1.1 booth 编码

1. radix2 booth encode
   在移位相加乘法中，我们可以直接跳过乘数中连续的0，因为被乘数乘以0也是0。而booth编码则允许我们将乘数中连续的n个1涉及的n次移位相加化简为一次移位相加与一次移位相减法，而增加乘数的稀疏度（增加0的数量）
   其中radix2的booth编码是
   

2. 乘以一个常数
   用到booth编码优化常数c的编码，或者做出一些其它优化，毕竟c是固定的。例如如果c=113，根据113=16(8-1)+1，我们可以把乘法过程优化为
   

3. radix4 booth encode
   我们也可以使用{0,a,2a,-a}代替{0,a,2a,3a}作为部分积，即将其中的3a代替为-a。这样就能避免 a+2a的计算。具体做法是，如果第i次迭代的部分积为3a，那我们就把这个部分积替代为-a，然后在第i+1迭代中补上这个-a。这样就能避免出现部分积为3a的情况，从而避免这个加法。但这么做可能导致乘法器最后必须多迭代一次（补上前一次迭代中的-a）
   
   

1.2 华莱士树

一般在做较多数字的加减法操作的时候我们会选择将这些操作数进行压缩，即找到2个数使得他们的和等效成原先的那组数，一般多组数据要通过华莱士数进行压缩，而华莱士树是由一系列的压缩器构成的。

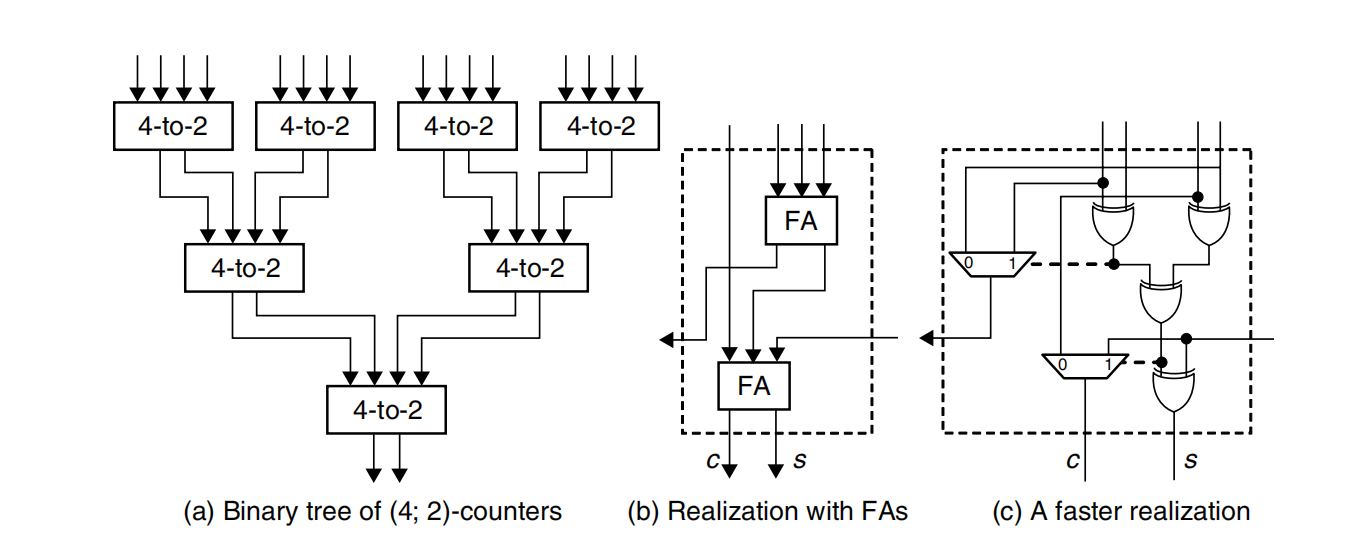
1.3 3-2压缩器

3-2压缩器的本质是全加器，或者说是一个保存进位的加法器(csa),其中的
sum = a ^ b ^ c
car = a&b | a&c | b&c
sum_out = 2car + sum = a + b + c

2. 小结

Booth 编码（Booth Encoding） 是一种用于优化二进制乘法运算的编码技术，由 Andrew Donald Booth 于 1951 年提出。其核心作用是减少乘法过程中加法运算的次数，尤其在带符号数（补码）乘法中能显著提升效率，广泛应用于处理器、数字信号处理器（DSP）等硬件设计中。

为什么需要 Booth 编码？

传统二进制乘法中，乘数的每一位（0 或 1）都会决定是否累加被乘数，若乘数存在连续多个 1，会导致多次重复加法（例如：1110₂表示需要 3 次累加)。
Booth 编码通过将乘数中连续的 1 转化为更简洁的编码形式，减少加法次数（如 1110₂可简化为 1 次加法和 1 次移位），从而降低硬件复杂度、缩短运算时间。