当前位置：首页 > news >正文

73. 矩阵置零

news 2025/7/26 7:24:28

题目

给定一个 m x n 的矩阵，如果一个元素为 0 ，则将其所在行和列的所有元素都设为 0 。请使用原地算法。

示例 1：

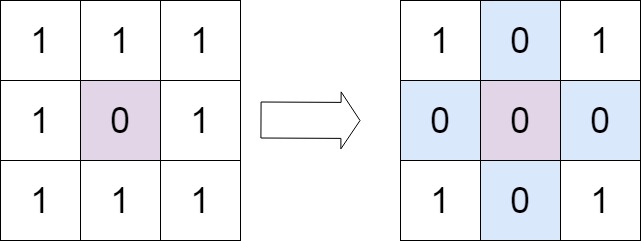
输入：matrix = [[1,1,1],[1,0,1],[1,1,1]]
输出：[[1,0,1],[0,0,0],[1,0,1]]

示例 2：

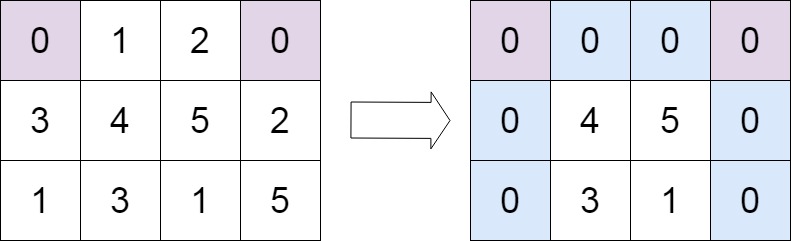
输入：matrix = [[0,1,2,0],[3,4,5,2],[1,3,1,5]]
输出：[[0,0,0,0],[0,4,5,0],[0,3,1,0]]

提示：

m == matrix.length
n == matrix[0].length
1 <= m, n <= 200
-231 <= matrix[i][j] <= 231 - 1

初步思路

最直观的方法是：

遍历矩阵，记录所有为 0 的元素的行和列。
然后根据记录的行和列，将对应的行和列的所有元素置为 0。

但这种方法需要额外的空间来存储这些行和列的信息。题目要求使用原地算法，因此我们需要找到一种不需要额外空间或仅使用常数空间的方法。

优化思路

为了不使用额外的空间，我们可以利用矩阵本身的第一行和第一列来标记哪些行和列需要被置为 0。具体步骤如下：

检查第一行和第一列是否有 0：
- 首先，我们检查第一行是否有 0，用 first_row_zero 标记。
- 然后，检查第一列是否有 0，用 first_col_zero 标记。
使用第一行和第一列作为标记：
- 遍历矩阵的其余部分（即从第二行第二列开始），如果 matrix[i][j] == 0，则将 matrix[i][0] 和 matrix[0][j] 设为 0。这表示第 i 行和第 j 列需要被置为 0。
根据标记置零：
- 再次遍历矩阵的其余部分，如果 matrix[i][0] == 0 或 matrix[0][j] == 0，则将 matrix[i][j] 设为 0。
处理第一行和第一列：
- 如果 first_row_zero 为真，则将第一行所有元素置为 0。
- 如果 first_col_zero 为真，则将第一列所有元素置为 0。

为什么这样做？

使用第一行和第一列作为标记可以避免使用额外的空间。
首先检查第一行和第一列是否有 0，是因为之后我们会用它们来标记其他行和列，所以需要先保存它们的状态。
通过将 matrix[i][0] 和 matrix[0][j] 设为 0 来标记，可以在后续步骤中知道哪些行和列需要被置零。

可能的误区

直接修改导致信息丢失：
- 如果直接遍历矩阵并在遇到 0 时立即将该行和列置为 0，会导致后续遍历时无法区分原始的 0 和新置的 0。
忽略第一行和第一列的初始状态：
- 如果不先检查第一行和第一列是否有 0，直接用它们作为标记，可能会丢失原始信息。

代码实现

以下是基于上述思路的伪代码：

def setZeroes(matrix):m = len(matrix)n = len(matrix[0]) if m > 0 else 0first_row_zero = any(matrix[0][j] == 0 for j in range(n))first_col_zero = any(matrix[i][0] == 0 for i in range(m))# 使用第一行和第一列作为标记for i in range(1, m):for j in range(1, n):if matrix[i][j] == 0:matrix[i][0] = 0matrix[0][j] = 0# 根据标记置零for i in range(1, m):for j in range(1, n):if matrix[i][0] == 0 or matrix[0][j] == 0:matrix[i][j] = 0# 处理第一行和第一列if first_row_zero:for j in range(n):matrix[0][j] = 0if first_col_zero:for i in range(m):matrix[i][0] = 0

示例验证

示例 1：

初始矩阵：

[[1,1,1],[1,0,1],[1,1,1]
]

first_row_zero = False (第一行没有 0)
first_col_zero = False (第一列没有 0)
标记：
- matrix[1][1] = 0，所以 matrix[1][0] = 0, matrix[0][1] = 0
- 标记后第一行和第一列：
  - 第一行：[1, 0, 1]
  - 第一列：[1, 0, 1]
根据标记置零：
- matrix[1][2]：matrix[1][0] == 0 → 置为 0
- matrix[2][1]：matrix[0][1] == 0 → 置为 0
- 其他位置不需要改变
结果：

[[1,0,1],[0,0,0],[1,0,1]
]

示例 2：

初始矩阵：

[[0,1,2,0],[3,4,5,2],[1,3,1,5]
]

first_row_zero = True (第一行有 0)
first_col_zero = True (第一列有 0)
标记：
- matrix[0][0] = 0：matrix[0][0] 已经是 0, matrix[0][0] 已经是 0
- matrix[0][3] = 0：matrix[0][3] 已经是 0, matrix[0][3] 已经是 0
- 没有其他 0
根据标记置零：
- 所有 matrix[i][j] 如果 matrix[i][0] == 0 或 matrix[0][j] == 0 则置为 0
- matrix[0][0] 和 matrix[0][3] 已经是 0
- matrix[1][0] 和 matrix[2][0]：因为 first_col_zero 会在后面处理
- matrix[1][3]：matrix[0][3] == 0 → 置为 0
- matrix[2][3]：matrix[0][3] == 0 → 置为 0
处理第一行和第一列：
- 第一行全部置为 0
- 第一列全部置为 0
结果：

[[0,0,0,0],[0,4,5,0],[0,3,1,0]
]

边界情况

空矩阵：矩阵的行或列为 0，直接返回。
单行或单列矩阵：
- 如 [[1, 0, 1]]，应变为 [[0, 0, 0]]。
- 如 [[1], [0], [1]]，应变为 [[0], [0], [0]]。
矩阵中无 0：矩阵不变。

复杂度分析

时间复杂度：O(m * n)，因为我们最多遍历矩阵三次（检查第一行和第一列，标记，置零）。
空间复杂度：O(1)，只使用了常数个额外变量。

最终代码

以下是基于上述思路的 C++ 实现代码：

#include <vector>
#include <algorithm>using namespace std;void setZeroes(vector<vector<int>>& matrix) {int m = matrix.size();if (m == 0) return;int n = matrix[0].size();bool firstRowZero = false;bool firstColZero = false;// 检查第一行是否有0for (int j = 0; j < n; ++j) {if (matrix[0][j] == 0) {firstRowZero = true;break;}}// 检查第一列是否有0for (int i = 0; i < m; ++i) {if (matrix[i][0] == 0) {firstColZero = true;break;}}// 使用第一行和第一列作为标记for (int i = 1; i < m; ++i) {for (int j = 1; j < n; ++j) {if (matrix[i][j] == 0) {matrix[i][0] = 0;matrix[0][j] = 0;}}}// 根据标记置零for (int i = 1; i < m; ++i) {for (int j = 1; j < n; ++j) {if (matrix[i][0] == 0 || matrix[0][j] == 0) {matrix[i][j] = 0;}}}// 处理第一行if (firstRowZero) {for (int j = 0; j < n; ++j) {matrix[0][j] = 0;}}// 处理第一列if (firstColZero) {for (int i = 0; i < m; ++i) {matrix[i][0] = 0;}}
}

代码解释

检查第一行和第一列是否有0：
- firstRowZero 标记第一行是否有0。
- firstColZero 标记第一列是否有0。
使用第一行和第一列作为标记：
- 遍历矩阵的其余部分（从第二行第二列开始），如果 matrix[i][j] == 0，则将 matrix[i][0] 和 matrix[0][j] 设为0。
根据标记置零：
- 再次遍历矩阵的其余部分，如果 matrix[i][0] == 0 或 matrix[0][j] == 0，则将 matrix[i][j] 设为0。
处理第一行和第一列：
- 如果 firstRowZero 为真，则将第一行所有元素置为0。
- 如果 firstColZero 为真，则将第一列所有元素置为0。

示例测试

#include <iostream>void printMatrix(const vector<vector<int>>& matrix) {for (const auto& row : matrix) {for (int num : row) {cout << num << " ";}cout << endl;}
}int main() {vector<vector<int>> matrix1 = {{1, 1, 1},{1, 0, 1},{1, 1, 1}};setZeroes(matrix1);printMatrix(matrix1);// 输出:// 1 0 1// 0 0 0// 1 0 1vector<vector<int>> matrix2 = {{0, 1, 2, 0},{3, 4, 5, 2},{1, 3, 1, 5}};setZeroes(matrix2);printMatrix(matrix2);// 输出:// 0 0 0 0// 0 4 5 0// 0 3 1 0return 0;
}