LeetCode 198 打家劫舍 LeetCode 213.打家劫舍II
LeetCode 198 打家劫舍
思路 :
类似于爬楼梯,不过爬楼梯求的是多少种方式/排列数。
打家劫舍与01背包的最大区别在于dp数组的定义,01背包的dp数组下标是背包容量,打家劫舍的dp数组下标是目前偷到第几个房屋。明确了这点之后,后续的初始化和递推公式就可以明确了。
Code:
class Solution(object):def rob(self, nums):""":type nums: List[int]:rtype: int"""### 1. dp数组定义。### dp[j] 表示偷到第j号房屋时的最高金额数dp = [0] * (len(nums))## 2. dp初始化。if len(nums) >= 1:dp[0] = nums[0] ##只偷第一个房屋if len(nums) >= 2:dp[1] = max(nums[0], nums[1]) ##偷到第二个房屋时的最大金额数,取决于前面两个那个金额数最高。## 3. 递推公式## dp[j] = max(dp[j-2]+nums[j], dp[j-1]).## dp[j] = dp[j-2]+nums[j] 表示到第j号房屋时选择偷,那就要将当前房屋的金额数算进去,并加上偷到j-2号房屋时的最大金额## dp[j] = dp[j-1] 表示到第j号房屋时,选择不偷第j号房屋## 4. 遍历顺序。由于dp编号跟房屋顺序有关,因此是顺序遍历if len(nums) == 1:return dp[0]elif len(nums) == 2:return dp[1]for i in range(2, len(nums)):dp[i] = max(nums[i] + dp[i-2], dp[i-1])## 5. 打印dp数组return dp[-1]LeetCode 213.打家劫舍II
在198的基础上进行限制,现在数组的开头和结尾是相邻的关系。如何解决环是这道题的关键。
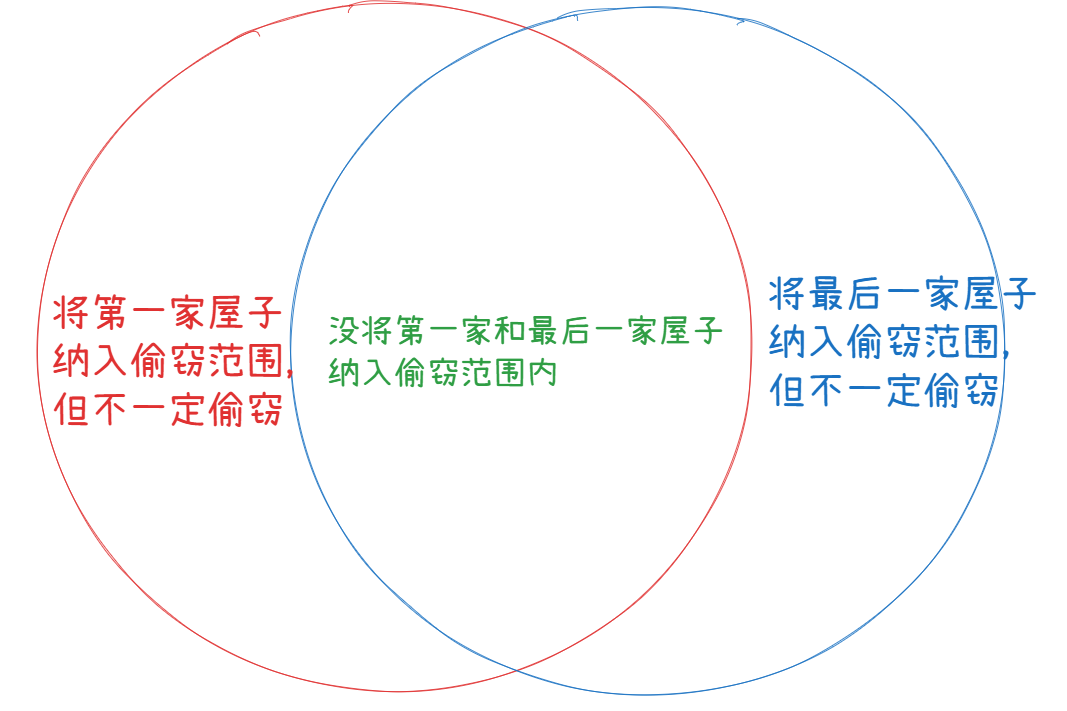
因为这道题的关键在于首尾,因此我们可以将其分为三种情况进行考虑。
- 没将第一家和最后一家屋子考虑在内。
- 将第一家屋子考虑在内,但没考虑最后一家屋子
- 将最后一家屋子考虑在内,但没考虑第一家屋子
其中情况1是情况2和情况3的子集,因为将第一家/最后一家考虑在内后,也可能不会对其进行偷窃。因此,只需要分别根据Leetcode 198的思路去分别求得情况2和情况3的最大金额数,然后取一个最大值,就可以得到最终的最优解了。(本题的关键在于首尾,那么将总的情况分为三种进行分析来获得每个情况的最优解,对每个情况的最优解取最大值就可以获得总情况的最优解。)
Code
class Solution(object):def rob(self, nums):""":type nums: List[int]:rtype: int"""if len(nums) == 1:return nums[0]if len(nums) == 2:return max(nums[0], nums[1])begin_nums = nums[0:len(nums)-1]final_nums = nums[1:len(nums)]begin_result = self.sub_rob(begin_nums)final_result = self.sub_rob(final_nums)return max(begin_result, final_result)def sub_rob(self, nums):## 1. dp定义。dp[j]表示偷到第j家的最高金额dp = [0]*len(nums)## 2. dp初始化。if len(nums) >= 1:dp[0] = nums[0]if len(nums) >= 2:dp[1] = max(nums[0], nums[1])## 3. 递推公式。 dp[j] = max(dp[j-2]+nums[j], dp[j-1])## 4. 遍历顺序for i in range(2, len(nums)):dp[i] = max(dp[i-2]+nums[i], dp[i-1])## 5. 打印dpreturn dp[-1]LeetCode 337.打家劫舍 III
上面两题都是数组,针对是的线性的操作。这道题是二叉树,涉及到树的遍历+dp数组构建。
思路:
针对一维数组的可以采用LeetCode 198的思路来进行处理。然而,针对多个维度的,如本题中的二叉树就有两个维度需要考虑(左子节点和右子节点),遇到这种多个维度的,需要通过遍历来进行完成,因此不好像leetCode 198那样直接定义一个定长的dp数组。
- 因此,我们只好通过判断当前节点偷还是不偷来定义一个dp数组,dp = [val_0, val_1],val_0表示为不偷当前节点时所偷的最大金额,val_1表示偷当前节点时所偷的最大金额。
- 另外,需要将多个维度的信息进行汇总,因此本题适合用后序遍历来进行遍历,并对最后的中间节点的最大金额数进行判断,以得到所能偷到的最大金额数目。
Code
# Definition for a binary tree node.
# class TreeNode(object):
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution(object):def rob(self, root):""":type root: Optional[TreeNode]:rtype: int"""result = self.traversal(root)return max(result[0], result[1])def traversal(self, node):# 1. dp数组定义。# 每个节点只有两种状态,偷还是不偷。# 因此,针对一个节点是否偷的金额数,可以用一个长度为2的dp数组来表示 当前节点不偷时的金额为0,当前节点偷时的金额为节点的值大小。# dp 表示当前节点不偷还是偷. dp = [0, node,val]# 2. dp初始化### dp = [0, 0];金额初始化为0,后续会根据递推结果进行修改# 3. 递推公式# dp = [val_0, val_1]# val_0 = max(leftdp[0], leftdp[1]) + max(rightdp[0], rightdp[1])# val_0 表示当前节点不偷,因此需要到子节点去判断,判断子节点偷还是不偷# val_1 = cur.val + leftdp[0] + rightdp[0]# val_1 表示节点偷,那金额就是当前节点的值;而其子节点就不能偷了# 4. 遍历方式(后续遍历,左右中。将值从底往上进行传递)if not node: ##终止条件,节点不存在,偷与不偷的结果得到的金额都是0return [0, 0]leftdp = self.traversal(node.left) # 左rightdp = self.traversal(node.right) # 右# 中# 当前节点——不偷# max(leftdp[0], leftdp[1]) 获得左子节点不偷和偷两种状态下的最大金额数目 ..val_0 = max(leftdp[0], leftdp[1]) + max(rightdp[0], rightdp[1])# 当前节点——偷val_1 = node.val + leftdp[0] + rightdp[0]# 5. 打印dp数组return [val_0, val_1] 