【数据结构】第一讲 —— 概论

【数据结构】第一讲 —— 概论

1.1 基本概念和常用术语

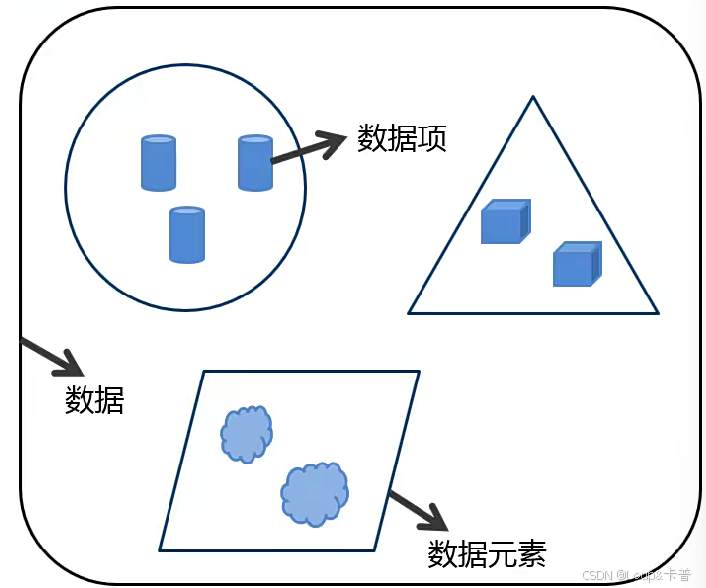
• 数据的基本单位是数据元素，最小单位是数据项
• 一个数据元素可以由若干个数据项组成

1.2 了解数据结构

1. 数据结构

定义：数据结构指的是数据元素之间的相互关系，即数据的组织形式
内容：数据的逻辑结构、数据的存储结构、数据的运算

2. 数据的逻辑结构

定义：从逻辑关系上描述数据，与数据元素的存储结构无关，独立于计算机
分类：线性结构和非线性结构

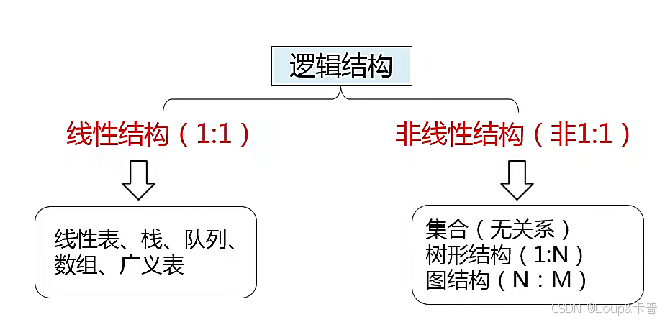
3. 数据的物理结构（存储结构）

定义：数据元素及其关系在计算机内的存储方式，称为数据的存储结构
实现方法：顺序存储、链接存储、索引存储、散列存储

4. 数据的运算

定义：对数据元素施加的操作（行为）
内容：最常用的插入、删除、查找、排序等。

插入：增加节点、入栈、入队
删除：删除节点、出栈、出队
查找：二分查找、散列查找
排序：选择排序、快速排序

1.3 算法的描述和分析

1.3.1 算法的描述

算法是对特定问题的求解方法（步骤）的一种描述，是指令的有限序列，其中每一条指令表示一个或多个操作

算法的五大基本准则：

• 有穷性：一个算法必须总是在执行有穷步之后结束，且每一步都在有穷时间内完成。
• 确定性：算法中每一条指令必须由确切的含义，不存在二义性
• 可行性：一个算法是能行的。即算法描述的操作都可以通过已经实现的基本运算执行有限次来实现。
• 输入：一个算法有零个或多个输入，这些输入取自于某个特定的对象集合
• 输出：一个算法有一个或多个输出，这些输出是同输入有着某些特定关系的量

1.3.2

算法的分析因素

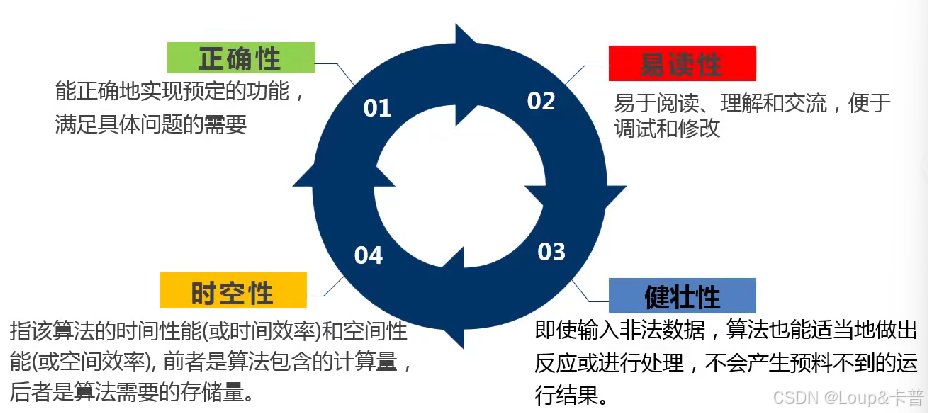
健壮性又叫鲁棒性

时间复杂度：
算法中基本操作重复执行的次数是问题规模n的某个函数，其时间量度记作T(n) = O(f(n)) ，称作算法的渐进时间复杂度（Asymptotic Time complexity)，简称时间复杂度。
一般地，常用最深层循环内地语句中原操作地执行频度（重复执行地次数）来表示。

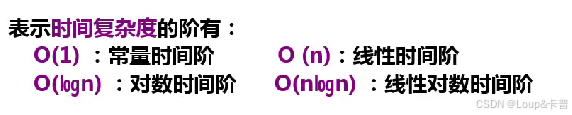
for (i = 1; i <= n; ++i) {++x;s+=x;
}

时间复杂度为：O(n) ，即为线性阶

for (i = 1; i <= n; ++i) {for (j = 1; j <= n; ++j) {++x; s+=x}
} 

时间复杂度为：O(n^2) ，即平方阶

for (i = 1; i <= n; ++i) {for (j = 1; j <= n; ++j) {c[i][j] = 0;for (k = 1; k <= n; ++k) {c[i][j] += a[i][k] * b[k][j];}} 
}

需要注意其中 c[i][j] = 0 不能纳入计算时间复杂度的语句。需要计算最深层循环c[i][j] += a[i][k] * b[k][j]; 的语句。
时间复杂度为：O(n^3) ，即为立方阶

空间复杂度

空间复杂度是指算法编写成程序后，在计算机中运行时所需存储空间大小的度量，该存储空间一般包括三个方面：

• 指令常数变量所占用的存储空间；
• 输入数据所占用的存储空间；
• 辅助（存储）空间。

一般地，算法的空间复杂度指的是辅助空间