相机模型和对极几何

一、相机模型

1.针孔相机模型-外参矩阵

1.世界坐标系到相机坐标系

• 世界坐标系：可以定义空间中任意一个位置，原点位置+三个坐标轴方向=坐标系姿态（X,Y,Z）
• 相机坐标系：定义在相机上，原点是相机中心，z轴沿着相机朝向，需要定义Y轴上下

点的世界坐标：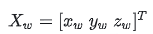

点相机坐标：

刚体变换：旋转+平移 -> 齐次坐标形式（两个坐标系的转换）

逆变换（相机坐标系到世界坐标系）：

2.相机中心在世界坐标系中的位置

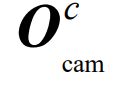：相机中心在相机坐标系中的坐标为0

相机中心在世界坐标系中的坐标

2.相机模型-内参矩阵

1.相机坐标系到归一化像平面坐标系

归一化像平面是虚拟的平面坐标，它与物理像平面平行，且距离相机光心距离为f=1

2.归一化像平面坐标系到物理像平面坐标系—小孔成像过程

3.归一化像平面到像素坐标系

一般以左上角为坐标原点，需要进行坐标系平移

整体转换流程如下所示：

3.2D-2D的对极几何约束

• x1, x2像素坐标
• x1^, x2^ 相机坐标

本质矩阵的对极约束是对相机坐标系下的对极约束。

基础矩阵的对极约束是对像素坐标系下的对极约束。

**3.1 **2D-2D:对极几何——基础矩阵F

性质：

• 3x3的矩阵，秩为2->不可逆
• 具有7个自由度，没有尺度少了一个自由度，秩为2少一个自由度
• 奇异值为： [𝜎1,𝜎2,0]𝑇
• 极线约束：

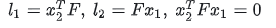
求解方法：

• 直接线性变换法
  • 8点法
  • 最小二乘法
• 基于RANSAC的鲁棒方法

3.2 2D-2D:对极几何——RANSAC

RANSAC——随机一致性采样

• N：样本点个数
• K：求解模型需要最少的点的个数
• 流程：
• 1）随机采样 K 个点
• 2）对该 K个点拟合模型
• 3）计算其它点到拟合模型的距离 小于一定阈值，当作内点，统计内点个数
• 4）重复 M 次，选择内点数最多的模型
• 5）利用所有的内点重新估计模型(可选)