C语言 --- 函数递归
函数递归
- 一、什么是函数递归
- 二、函数递归的要点
- 三、示例
- 1.计算n的阶乘
- 2.提取一个任意正整数的所有位数,按顺序排列
- 3.获取第n个斐波那契数,最开始的两个数是1,1
- 四、总结
一、什么是函数递归
函数递归是一种解决问题的思想,是将一个大的问题化为一个一个小的问题(类似于剥洋葱),是在一个函数体内部自己调用自己的方法。递归就是递推加回归,是基于函数实现的。
例如:
// 第一个最简单的函数递归程序:int main()
{printf("hahaha\n");main(); // 在main函数体内再次调用自己,这就是递归return 0;
}
运行结果:
但是这是一个问题程序,因为没有临界条件,所以会死递归下去,最终导致出现上图中栈溢出(Stack overflow)。
因为每一次函数递归都会创建函数栈帧,此栈帧创建在内存的栈区,最终死递归,栈区空间消耗完毕,出现栈溢出的问题。
二、函数递归的要点
基于点一,函数递归有以下两个要点:
1. 函数递归要有临界条件,每次递归后都要逼近此条件,否则会出现死递归的情况,到达临界条件,将不再函数调用
2. 并不是所有的程序都能写成函数递归形式,并且就算是能写成函数递归的形式,在函数递归调用过程中会创建函数栈帧,产生运行时的开销(空间,时间),空间可能出现栈溢出的问题,时间影响运行效率,所以在某些程序中迭代(循环)和递归形式都能实现,并且递归实现代码比迭代实现更加复杂,那么还是使用迭代实现。
三、示例
1.计算n的阶乘
实现思路:

// 示例1:设计一个程序,计算n的阶乘
int func(int n)
{if (n == 0)return 1;elsereturn func(n - 1) * n;
}int main()
{// 计算n的阶乘int n = 0;scanf("%d", &n);int ret = func(n);printf("%d\n", ret);return 0;
}
递归过程:
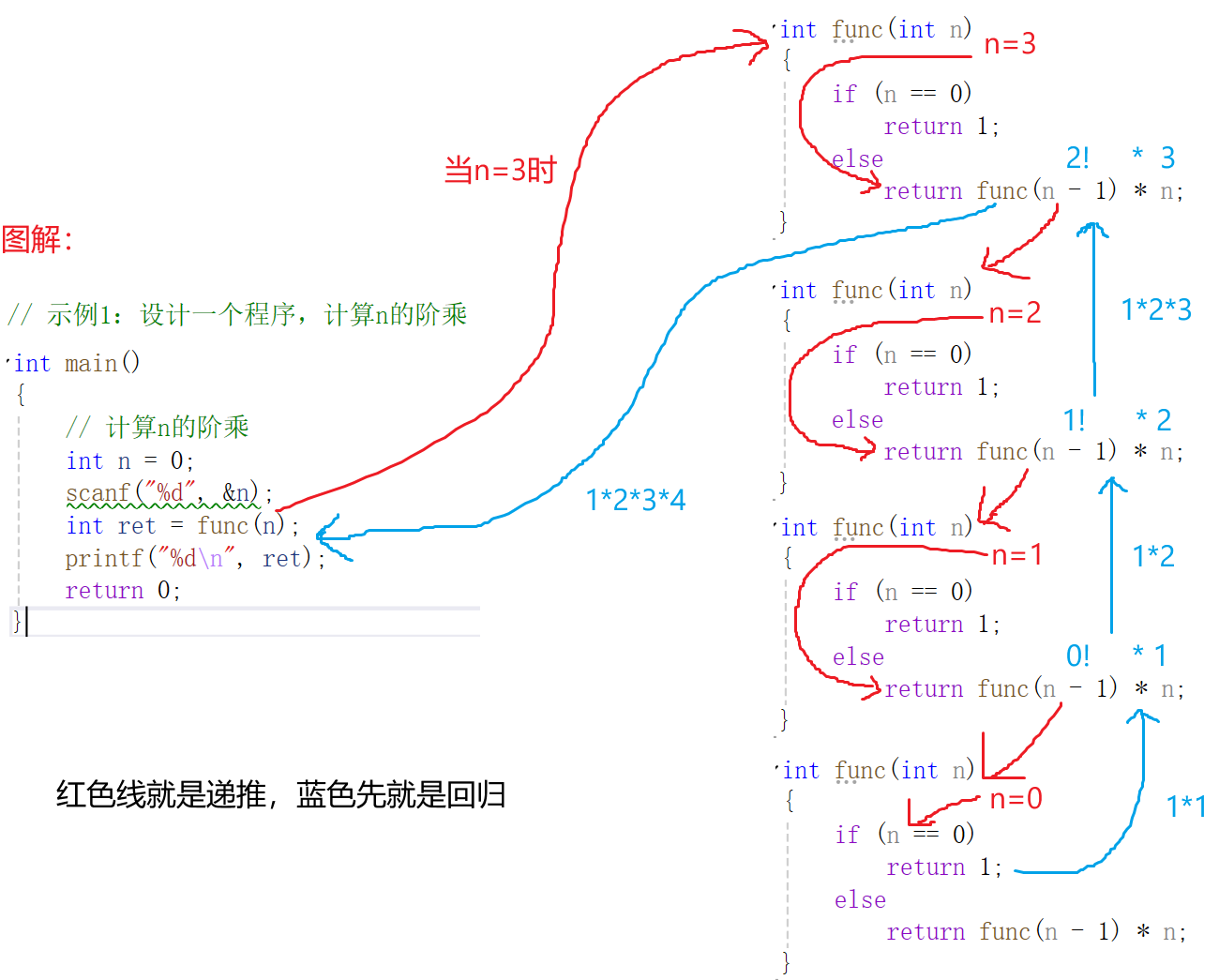
2.提取一个任意正整数的所有位数,按顺序排列
实现思路:

// 示例2:设计一个程序,提取一个任意正整数的所有位数,按顺序排列
void func(int m)
{// 当m为一位数时,直接提取自身if (m >= 0 && m <= 9)printf("%d ", m % 10);else{func(m / 10);printf("%d ", m % 10);}
}int main()
{int m = 0;scanf("%d", &m);func(m);return 0;
}递归过程:
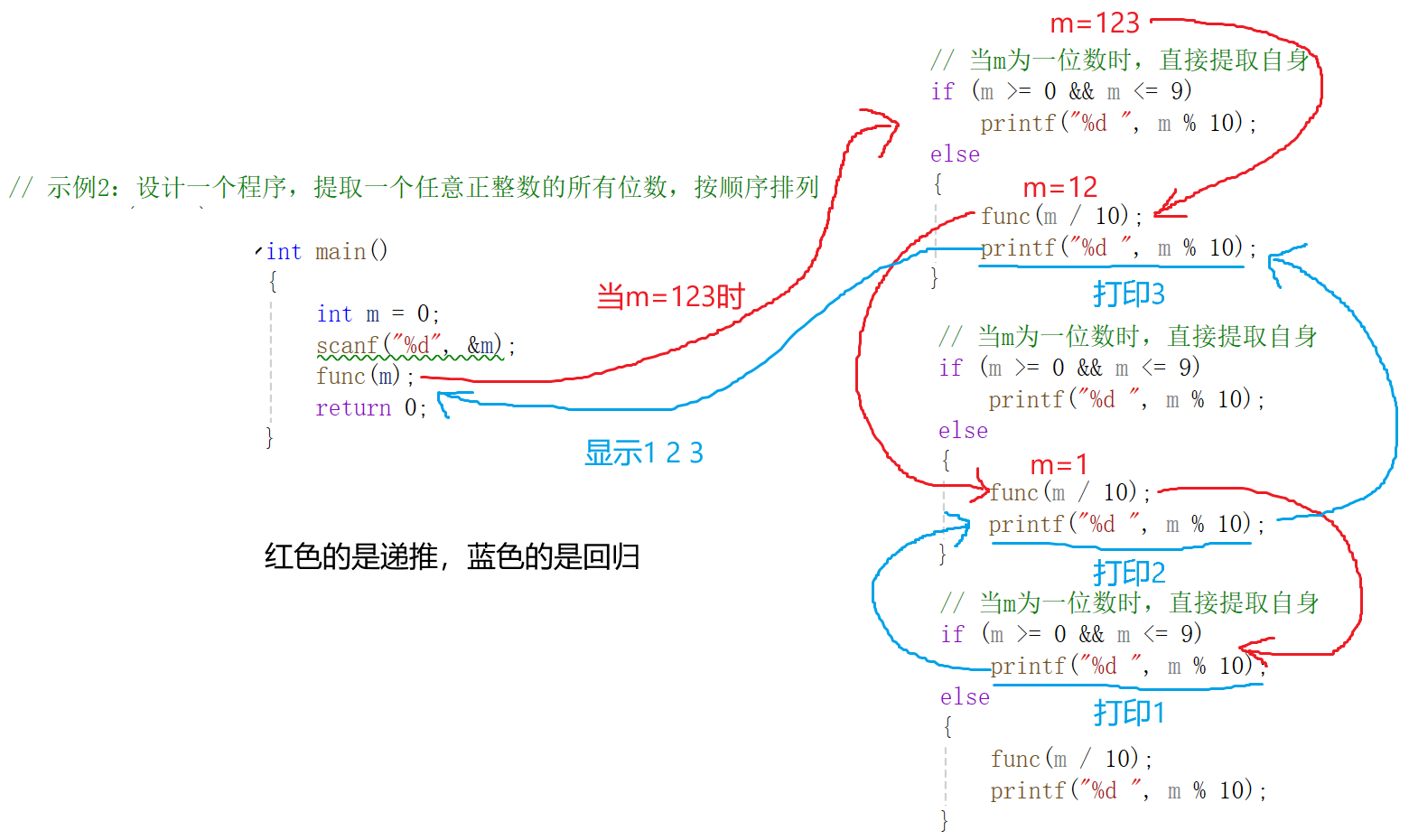
3.获取第n个斐波那契数,最开始的两个数是1,1
实现思路:

// 示例3:设计一个程序,获取第n个斐波那契数,最开始的两个数是1,1
int fib(int n)
{if (n == 1 || n == 2){return 1;}else{return fib(n - 1) + fib(n - 2);}
}int main()
{int n = 0;scanf("%d", &n);int ret = fib(n);printf("%d\n", ret);return 0;
}这里直接说出结果,这是一个有问题的递归程序,当n很大很大的时候,上述代码执行效率非常低下,因为:
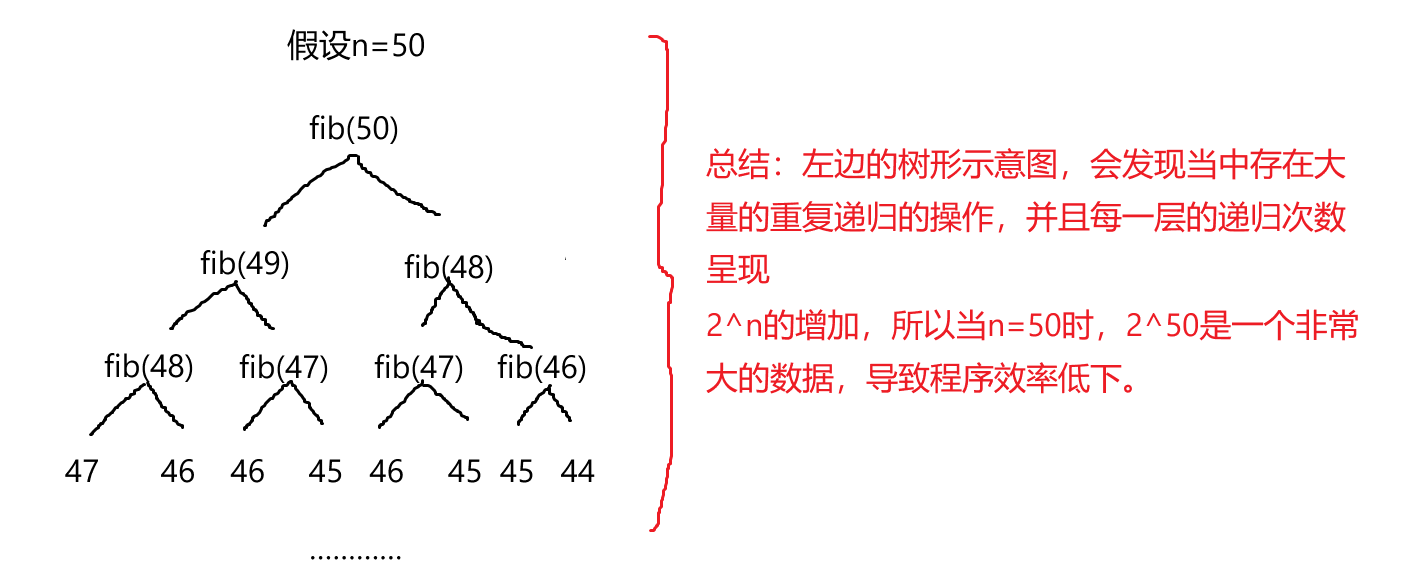
所以这就是一个逻辑思维上运用递归的思想,但是递归实现出来有些许问题,正确的思路:
定文三个变量,a,b,c,让a等于0位置上的数据,b等于1位置上的数据,c等中于a加上b的数据,c就是我们所求的第n个斐波那契数。之后再先让b的值赋值给给a,c的值赋值给给b,循环下去,直到n>2才结束。最后返回c。
int fib(int n) {// 定义三个变量,a,b,c// a是第一个数字1,b是第二个数字1// c是我们所需要的第n个斐波那契数int a=1, b=1,c;// 当所求斐波那契数是前两个的时候,直接给定值即可if(n == 1 && n == 2)c=a; // 此时斐波那契数就是1// 当所求斐波那契数是从第三个开始时while(n > 2){c = a + b;// 更新数据,注意别出现数据覆盖的情况a = b;b = c;n--; }// 返回斐波那契数return c;}
四、总结
上述的递归演示,第一个main函数内部再次调用自己导致出现栈溢出的错误是因为没有设定临界条件;前两个示例演示了如何分析一个程序如何变成递归思想,并且理清它的递归调用关系;最后一个示例就演示了在某写可以写成递归的程序,但是递归的实现有问题的这种程序,建议是使用迭代的思想去实现。
