线性表数据结构-堆栈

简称为栈。一种线性表数据结构，是一种只允许在表的一端进行插入和删除操作的线性表。

一、介绍

我们把栈中允许插入和删除的一端称为 「栈顶（top）」；另一端则称为 「栈底（bottom）」。当表中没有任何数据元素时，称之为 「空栈」。

堆栈有两种基本操作：「插入操作」 和 「删除操作」。

• 栈的插入操作又称为「入栈」或者「进栈」。
• 栈的删除操作又称为「出栈」或者「退栈」

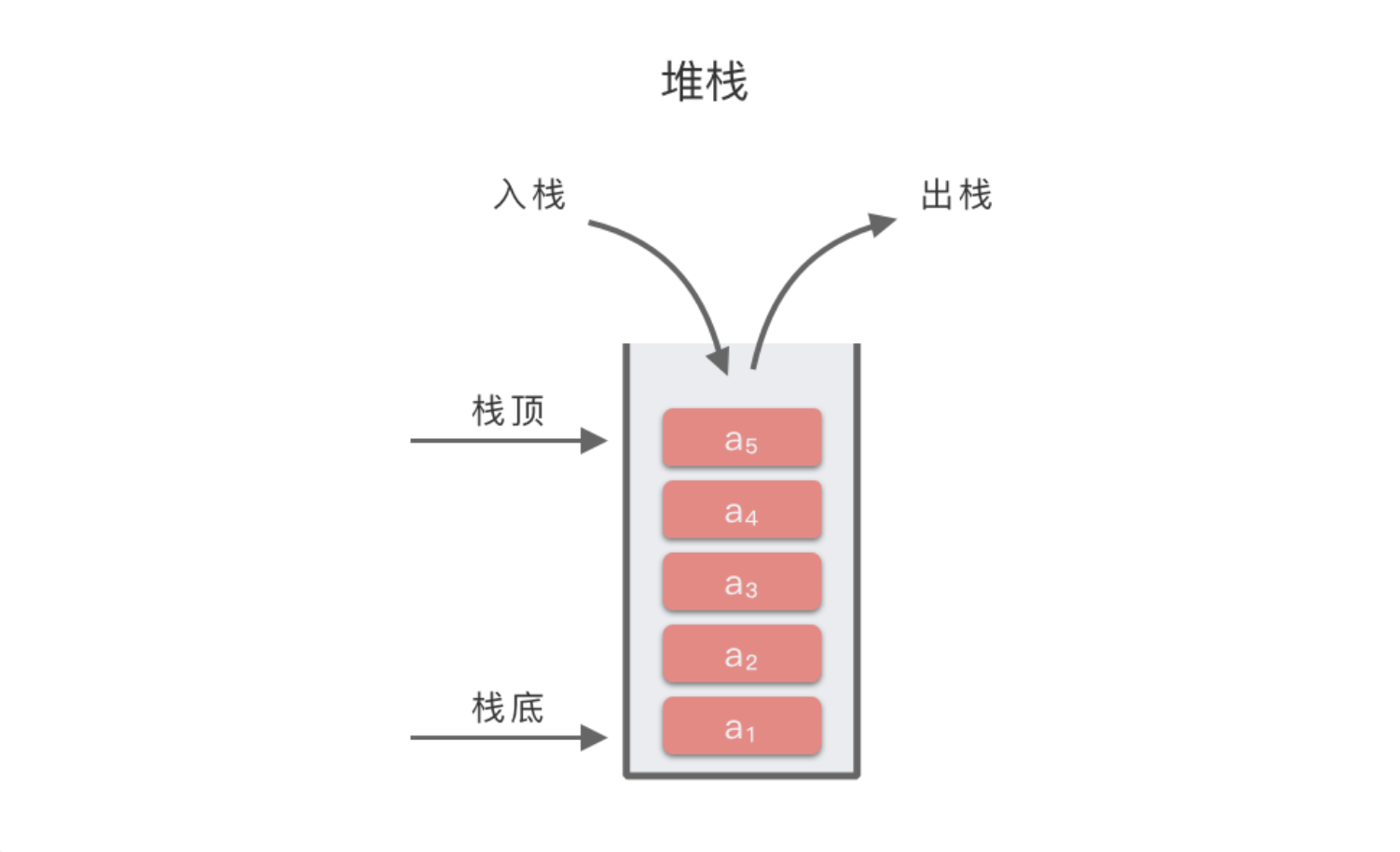
简单来说，栈是一种 「后进先出（Last In First Out）」 的线性表，简称为 「LIFO 结构」。

我们可以从两个方面来解释一下栈的定义：

• 第一个方面是 「线性表」。

栈首先是一个线性表，栈中元素具有前驱后继的线性关系。栈中元素按照 a1,a2,...,an的次序依次进栈。栈顶元素为 an。

• 第二个方面是 「后进先出原则」。

根据堆栈的定义，每次删除的总是堆栈中当前的栈顶元素，即最后进入堆栈的元素。而在进栈时，最先进入堆栈的元素一定在栈底，最后进入堆栈的元素一定在栈顶。也就是说，元素进入堆栈或者退出退栈是按照「后进先出（Last In First Out）」的原则进行的。

二、堆栈的顺序存储与链式存储

栈作为一种线性表来说，理论上应该具备线性表所有的操作特性，但由于「后进先出」的特殊性，所以针对栈的操作进行了一些变化。尤其是插入操作和删除操作，改为了入栈（push）和出栈（pop）

1. 堆栈的基本操作

1.1. 初始化空栈

创建一个空栈，定义栈的大小 size，以及栈顶元素指针 top。

1.2. 判断栈是否为空

当堆栈为空时，返回 True。当堆栈不为空时，返回 False。一般只用于栈中删除操作和获取当前栈顶元素操作中。

1.3. 判断栈是否已满

当堆栈已满时，返回 True，当堆栈未满时，返回 False。一般只用于顺序栈中插入元素和获取当前栈顶元素操作中。

1.4. 插入元素（进栈、入栈）

相当于在线性表最后元素后面插入一个新的数据元素。并改变栈顶指针 top 的指向位置。

删除元素（出栈、退栈）：相当于在线性表最后元素后面删除最后一个数据元素。并改变栈顶指针 top 的指向位置。

1.5. 获取栈顶元素

相当于获取线性表中最后一个数据元素。与插入元素、删除元素不同的是，该操作并不改变栈顶指针 top 的指向位置

1.6. 代码（顺序存储）

class Stack {constructor(size) {this.size = size; // 栈的大小this.top = -1;   // 栈顶指针，初始为空栈this.data = new Array(size);}// 判断栈是否为空isEmpty() {return this.top === -1;}// 判断栈是否已满isFull() {return this.top === this.size - 1;}// 插入元素（入栈）push(item) {if (this.isFull()) {console.log("栈已满，无法插入元素。");} else {this.data[++this.top] = item;}}// 删除元素（出栈）pop() {if (this.isEmpty()) {console.log("栈为空，无法删除元素。");return undefined;} else {const item = this.data[this.top];this.data[this.top] = undefined; // 清除已出栈元素的引用this.top--;return item;}}// 获取栈顶元素peek() {if (this.isEmpty()) {console.log("栈为空，无法获取栈顶元素。");return undefined;} else {return this.data[this.top];}}
}// 示例用法
const stack = new Stack(5); // 创建一个最大容量为5的栈console.log(stack.isEmpty()); // true，栈为空
console.log(stack.isFull());  // false，栈不满stack.push(1); // 入栈1
stack.push(2); // 入栈2console.log(stack.peek()); // 2，获取栈顶元素stack.pop(); // 出栈2console.log(stack.peek()); // 1，获取栈顶元素stack.push(3); // 入栈3
stack.push(4); // 入栈4
stack.push(5); // 入栈5console.log(stack.isFull()); // true，栈已满
stack.push(6); // 栈已满，无法插入元素

2. 堆栈的链式存储实现

堆栈的顺序存储结构保留着顺序存储分配空间的固有缺陷，即在栈满或者其他需要重新调整存储空间时需要移动大量元素。为此，堆栈可以采用链式存储方式来实现。

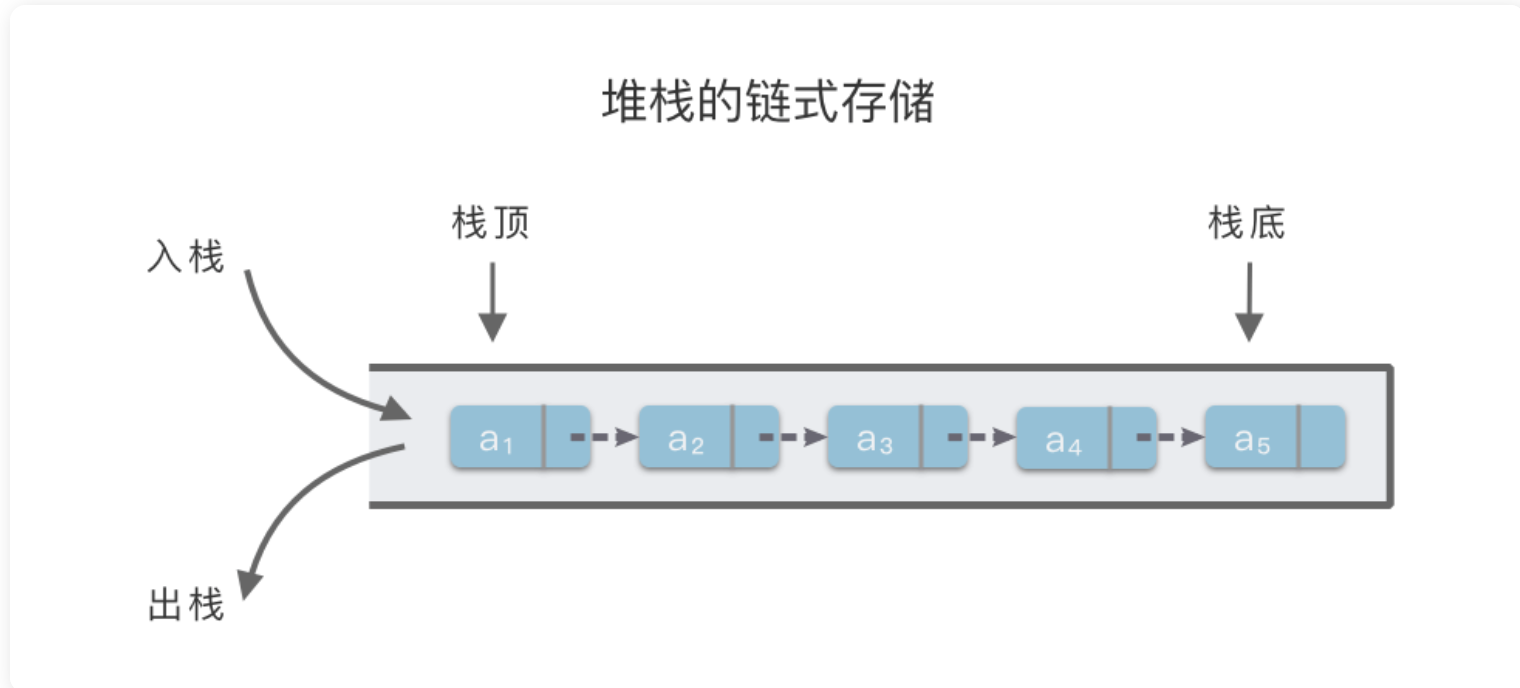
2.1. 堆栈的链式存储基本描述

我们约定 self.top 指向栈顶元素所在位置

• 初始化空栈：使用列表创建一个空栈，并令栈顶元素指针 self.top 指向 None，即 self.top = None。
• 判断栈是否为空：当 self.top == None 时，说明堆栈为空，返回 True，否则返回 False。
• 插入元素（进栈、入栈）：创建值为 value 的链表节点，插入到链表头节点之前，并令栈顶指针 self.top 指向新的头节点。
• 删除元素（出栈、退栈）：先判断堆栈是否为空，为空直接抛出异常。如果堆栈不为空，则先使用变量 cur 存储当前栈顶指针 self.top 指向的头节点，然后令 self.top 沿着链表移动 1 位，然后再删除之前保存的 cur 节点。
• 获取栈顶元素：先判断堆栈是否为空，为空直接抛出异常。不为空则返回 self.top 指向的栈顶节点的值，即 self.top.value

2.2. 代码

class Node {constructor(value) {this.value = value;this.next = null;}
}class Stack {constructor() {this.top = null; // 初始化空栈}// 判断栈是否为空isEmpty() {return this.top === null;}// 入栈操作push(value) {const newNode = new Node(value);newNode.next = this.top;this.top = newNode;}// 出栈操作pop() {if (this.isEmpty()) {throw new Error('Stack is empty');} else {const removedNode = this.top;this.top = this.top.next;removedNode.next = null; // 释放被移除节点的引用}}// 获取栈顶元素peek() {if (this.isEmpty()) {throw new Error('Stack is empty');} else {return this.top.value;}}
}// 示例用法:
const myStack = new Stack();
myStack.push(1);
myStack.push(2);
myStack.push(3);console.log(myStack.peek()); // 输出: 3 (栈顶元素)
myStack.pop();
console.log(myStack.peek()); // 输出: 2 (栈顶元素)

3. 练习题

给出由小写字母组成的字符串 S，重复项删除操作会选择两个相邻且相同的字母，并删除它们。

在 S 上反复执行重复项删除操作，直到无法继续删除。

在完成所有重复项删除操作后返回最终的字符串。答案保证唯一。

示例：

输入："abbaca" 输出："ca" 解释： 例如，在 "abbaca" 中，我们可以删除 "bb" 由于两字母相邻且相同，这是此时唯一可以执行删除操作的重复项。之后我们得到字符串 "aaca"，其中又只有 "aa" 可以执行重复项删除操作，所以最后的字符串为 "ca"。

3.1. 思路

我们可以发现，当字符串中同时有多组相邻重复项时，我们无论是先删除哪一个，都不会影响最终的结果。因此我们可以从左向右顺次处理该字符串。

而消除一对相邻重复项可能会导致新的相邻重复项出现，如从字符串 abba 中删除 bb 会导致出现新的相邻重复项 aa 出现。因此我们需要保存当前还未被删除的字符。一种显而易见的数据结构呼之欲出：栈。我们只需要遍历该字符串，如果当前字符和栈顶字符相同，我们就贪心地将其消去，否则就将其入栈即可

3.2. 代码

const removeDuplicates = (s) => {const stack = []; // 创建一个空数组作为栈for (const ch of s) { // 遍历输入字符串 s 中的每个字符if (stack.length && stack[stack.length - 1] === ch) {// 如果栈不为空且当前字符与栈顶字符相同，说明遇到了重复字符stack.pop(); // 从栈中移除栈顶的字符，相当于删除了重复字符} else {stack.push(ch); // 否则，将当前字符压入栈}}return stack.join(''); // 将栈中的字符拼接成字符串并返回
};

三、单调栈

一种特殊的栈。在栈的「先进后出」规则基础上，要求「从 栈顶 到 栈底 的元素是单调递增（或者单调递减）」。其中满足从栈顶到栈底的元素是单调递增的栈，叫做「单调递增栈」。满足从栈顶到栈底的元素是单调递减的栈，叫做「单调递减栈」

1. 单调递增栈

只有比栈顶元素小的元素才能直接进栈，否则需要先将栈中比当前元素小的元素出栈，再将当前元素入栈。

这样就保证了：栈中保留的都是比当前入栈元素大的值，并且从栈顶到栈底的元素值是单调递增的

[7, 6, 4, 2]。因为从栈顶（右端）到栈底（左侧）元素的顺序为 2, 4, 6, 7，满足递增关系，所以这是一个单调递增栈，向栈内插入元素4会发生什么

1.1. 思路

• 假设当前进栈元素为 x，如果 x 比栈顶元素小，则直接入栈。
• 否则从栈顶开始遍历栈中元素，把小于 x 或者等于 x 的元素弹出栈，直到遇到一个大于 x 的元素为止，然后再把 x 压入栈中。

1.2. 代码

class MonotonicStack {constructor() {this.stack = [];}// 插入元素并保持单调递增性质insertIntoIncreasingStack(element) {// 循环弹出比插入元素小的元素while (this.stack.length > 0 && element < this.stack[this.stack.length - 1]) {this.stack.pop();}// 插入元素this.stack.push(element);}// 获取栈中的元素getStack() {return this.stack;}
}// 测试代码
const stack = new MonotonicStack();
stack.insertIntoIncreasingStack(7);
stack.insertIntoIncreasingStack(6);
stack.insertIntoIncreasingStack(4);
stack.insertIntoIncreasingStack(2);console.log(stack.getStack()); // 输出: [7, 6, 4, 2]stack.insertIntoIncreasingStack(4);console.log(stack.getStack()); // 输出: [7, 6, 4, 4]

2. 单调递减栈

只有比栈顶元素大的元素才能直接进栈，否则需要先将栈中比当前元素大的元素出栈，再将当前元素入栈。

这样就保证了：栈中保留的都是比当前入栈元素小的值，并且从栈顶到栈底的元素值是单调递减的

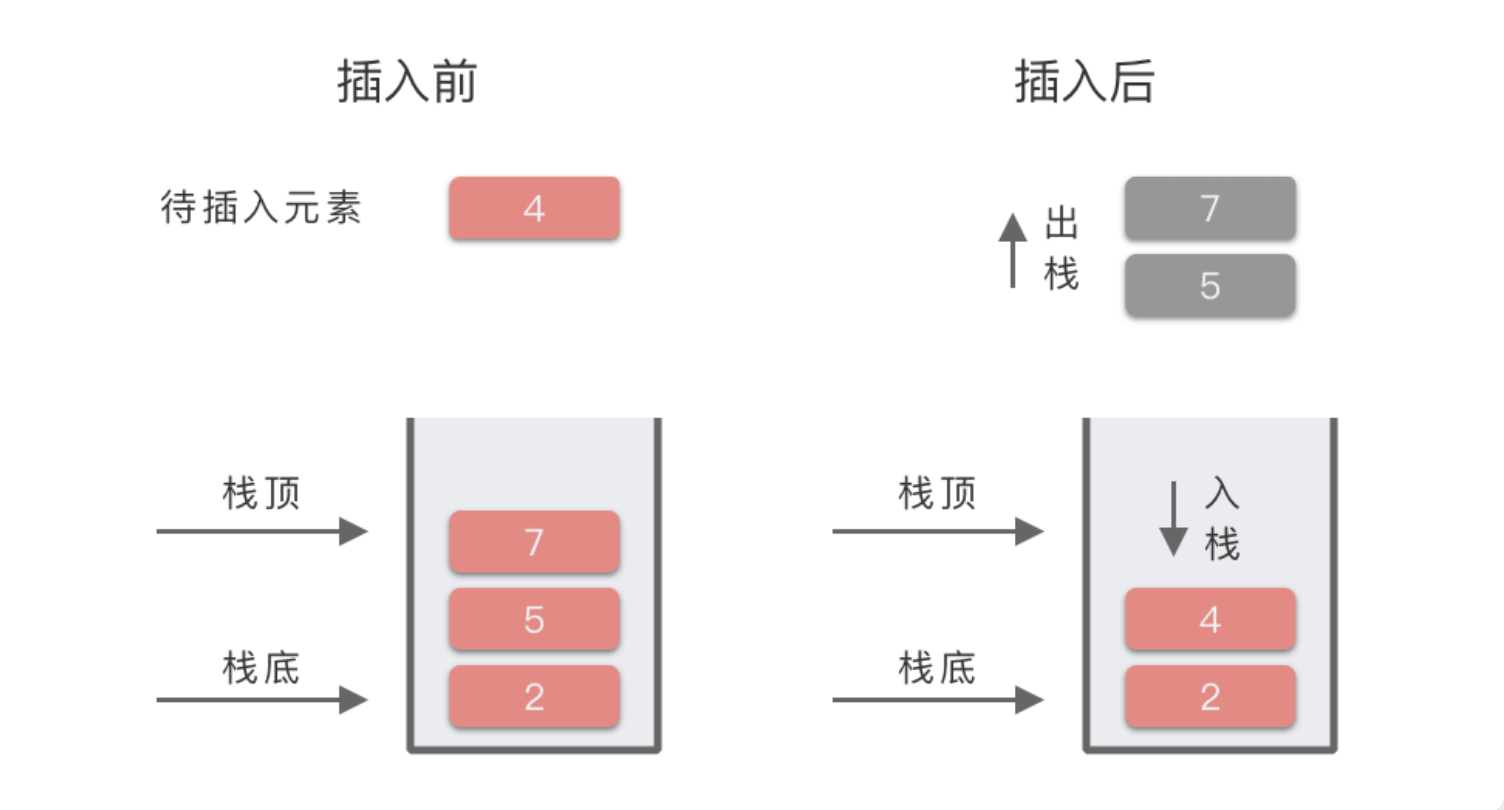
[2,5,7]。因为从栈顶（右端）到栈底（左侧）元素的顺序为 7,5,2，满足递减关系，所以这是一个单调递减栈，向栈内插入元素4会发生什么

2.1. 思路

• 假设当前进栈元素为 x，如果 x 比栈顶元素大，则直接入栈。
• 否则从栈顶开始遍历栈中元素，把大于 x 或者等于 x 的元素弹出栈，直到遇到一个小于 x 的元素为止，然后再把 x 压入栈中

2.2. 思路图

——未完待续——

视频教程