当前位置：首页 > java >正文

连续概率分布（拉普拉斯分布）

java 2025/8/23 8:21:48

一、说明

类似于高斯分布，还有其他的对称负指数分布，比如柯西分布，拉普拉斯分布，本篇讲述拉普拉斯分布。

二、基本概念

在概率论和统计学中，拉普拉斯分布是一种连续概率分布，以皮埃尔-西蒙·拉普拉斯的名字命名。它有时也称为双指数分布，因为它可以被认为是两个指数分布背靠背沿 x 轴拼接在一起。

2.1 密度函数

随机变量具有拉普拉斯 $\operatorname {laplace} (\mu ,b)$ 分布，如果其概率密度函数pdf为
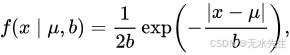
在这里插入图片描述
在这里

$\mu$ 是位置参数.用于确定分布的中心
并且 $b>0$ ，用于控制分布的散布或宽度,有时被称为“多样性”，是一个尺度参数。

如果 $\mu =0$ 和 $b=1$ ，正半线恰好是按 1/2 缩放的指数分布。

2.2 分布函数

由于使用了绝对值函数，拉普拉斯分布很容易积分（如果区分两种对称情况）。其累积分布函数如下：
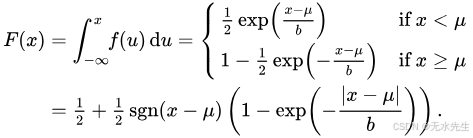
在这里插入图片描述

三、Python 中的示例

具有不同μ的拉普拉斯分布
下面的第一个代码是一个 Python 脚本，它说明了具有不同 μ 值（位置参数）的拉普拉斯分布。

import numpy as np
import matplotlib.pyplot as plt# Define the Laplacian distribution function
def laplacian_pdf(x, mu, b):return (1 / (2 * b)) * np.exp(-np.abs(x - mu) / b)# Values of the location parameter 'mu'
mu_values = [-2, 0, 2]
b = 1  # Fixed scale parameter# Create a range of x values
x = np.linspace(-10, 10, 1000)# Plot the Laplacian distributions for varying mu
plt.figure(figsize=(12, 6))for mu in mu_values:y = laplacian_pdf(x, mu, b)plt.plot(x, y, label=f'μ = {mu}')plt.title('Laplacian Distribution with Varying μ')
plt.xlabel('x')
plt.ylabel('Probability Density')
plt.legend()
plt.grid(True)
plt.show()

这是上述代码的输出：
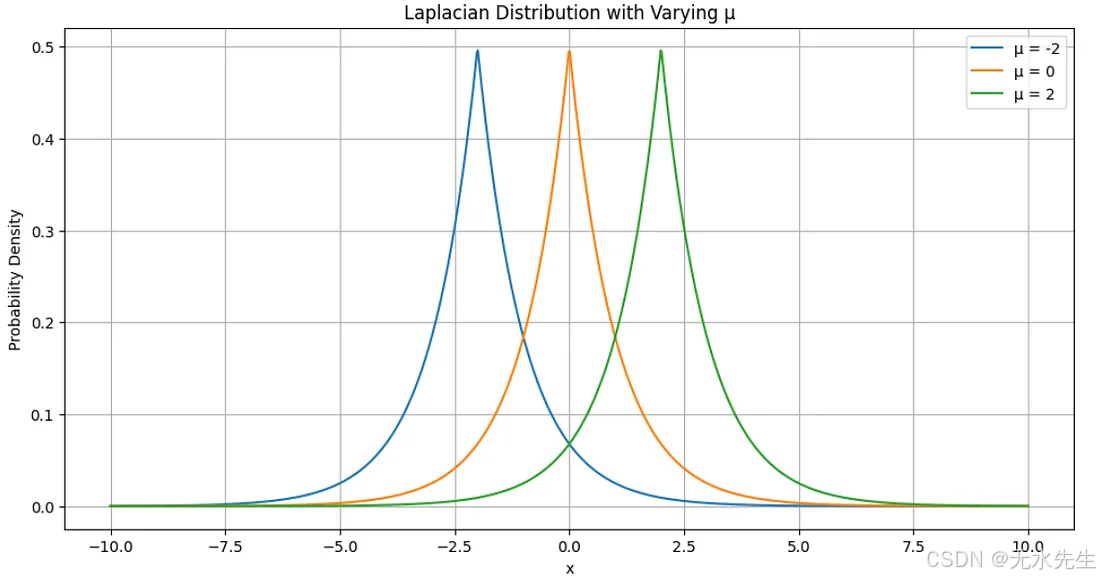
在这里插入图片描述

此脚本绘制位置参数 μ 不同值的拉普拉斯分布，其中具有固定尺度参数 b=1。
该函数计算中每个 μ 值的概率密度laplacian_pdf。

具有变化 b 的拉普拉斯分布
下面的第二段代码是一个 Python 脚本，它说明了具有不同 b （scale 参数）值的拉普拉斯分布。

import numpy as np
import matplotlib.pyplot as plt# Define the Laplacian distribution function
def laplacian_pdf(x, mu, b):return (1 / (2 * b)) * np.exp(-np.abs(x - mu) / b)# Values of the scale parameter 'b'
b_values = [0.5, 1, 2]
mu = 0  # Fixed location parameter# Create a range of x values
x = np.linspace(-10, 10, 1000)# Plot the Laplacian distributions for varying b
plt.figure(figsize=(12, 6))for b in b_values:y = laplacian_pdf(x, mu, b)plt.plot(x, y, label=f'b = {b}, σ = {np.sqrt(2)*b:.2f}')plt.title('Laplacian Distribution with Varying b')
plt.xlabel('x')
plt.ylabel('Probability Density')
plt.legend()
plt.grid(True)
plt.show()

这是上述代码的输出：

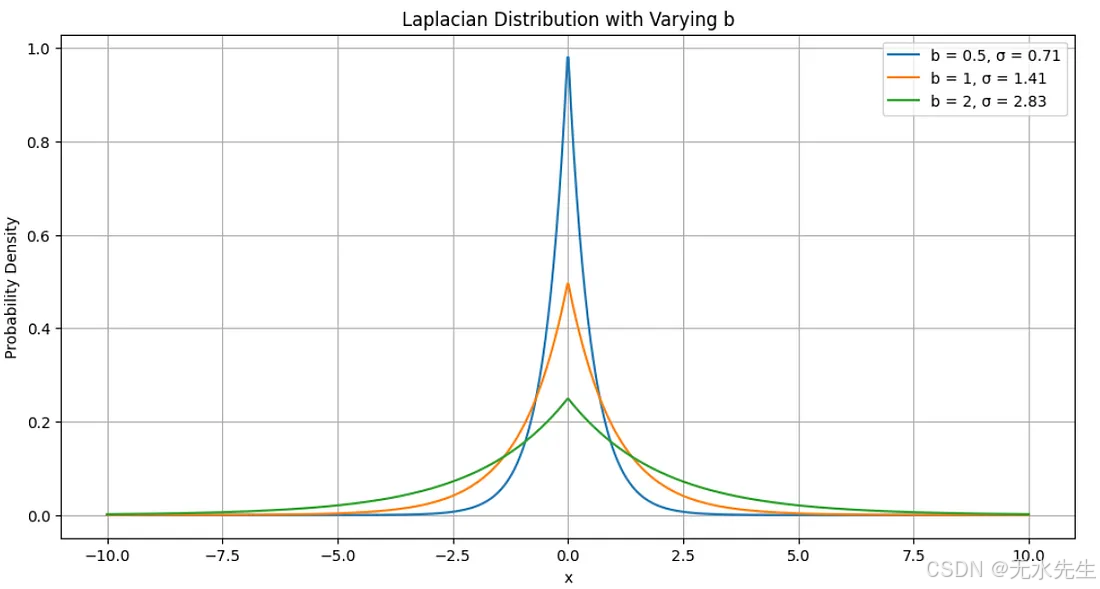
在这里插入图片描述