现代计算机图形学Games101入门笔记(三)
三维变换

具体形式缩放,平移

特殊点旋转。这里涉及到坐标系,先统一定义右手坐标系,根据叉乘和右手螺旋判定方向。这里还能法线Ry Sina 正负与其他两个旋转不一样。这里可以用右手螺旋,x叉乘z,发现大拇指朝下,与y轴向反,所以y轴特殊。

三维组合旋转


学的这些怎么用,用在视图/相机 变换。想象一下拍照,先大好场景,再摆好相机,再把3D的场景变成2D的图像。

视图变换
定义一个位置,还需要一个方向,还要一个相机的顶朝向,不然有可能倒着拍照。

这里相机和模型之间会形成相对关系。动相机和动模型,看到的能一样。

为了计算,在变换相机位置到空间坐标,那相应也要调整模型到相应的位置,才能保持图像不变。

变换换算成数学矩阵。这里旋转矩阵是正交矩阵,所以它的逆就是它的转置。


重新理解一下MVP,拍照物体成像过程。上面为了计算假设相机不动,在原点,形成x,y,z坐标系。那移动相机的变换,其实也是移动物体的变换。当然这个移动变换不是3D模型变换,是视图变换。

投影变换(正交、透视)


正交投影
这里需要跟上面视图变换关联起来,相机位置在原点,相机的朝向是-z,顶是y轴。然后来搞物体投影过来的变换。这里投影我们规定一个[-1,1]正方形区间。这个1也很特殊,跟矩阵里的齐次坐标刚好关联,这也是不是2,不是4,而是1,也是为了计算方便。



为啥有左手坐标系,就是发现右手坐标系在投影变换中,投影越远的,值反而小。

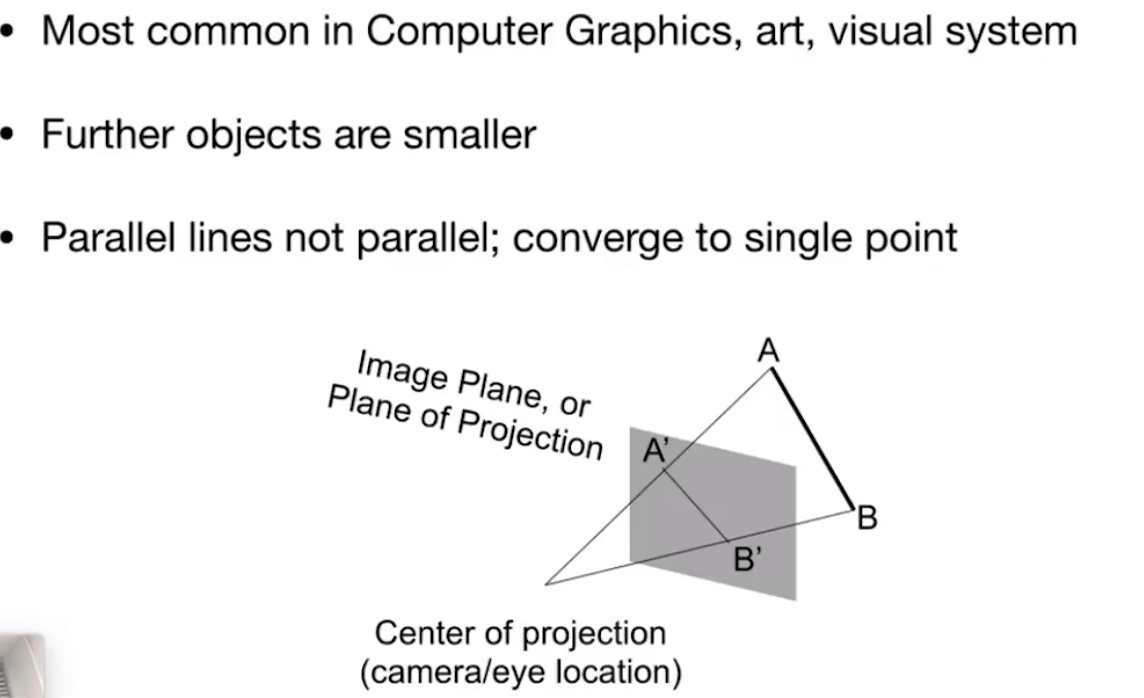
透视投影
满足近远小,平行线不平行,中心点就是相机位置。

这里1表示是点。点的齐次代表的同一个点。

正交投影,直接齐次到(1,-1)平方坐标就行。研究一下透视。

侧面观察,相似三角形

所以



挤压是不会影响物体z值的变化。


