树 Part 4

二叉树特点

■每个结点最多有两棵子树，所以二叉树中不存在度大于2的结点。注意不是只有两棵子树，而是最多有。没有子树或者有一棵子树都是可以的。

■左子树和右子树是有顺序的，次序不能任意颠倒。就像人是双手、双脚，但显然左手、左脚和右手、右脚是不一样的，右手戴左手套、右脚穿左鞋都会极其别扭和难受。

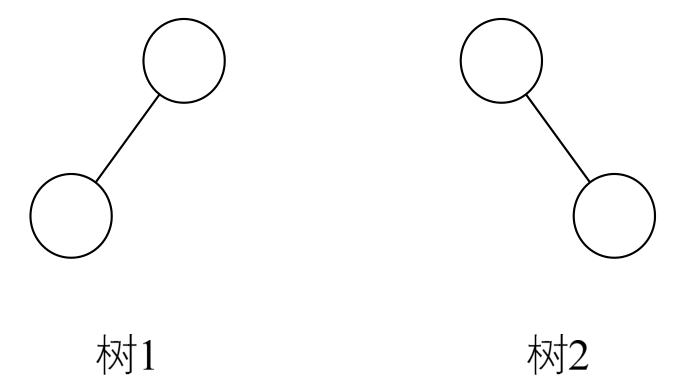
■即使树中某结点只有一棵子树，也要区分它是左子树还是右子树。图中，树1和树2是同一棵树，但它们却是不同的二叉树。就好像你一不小心，摔伤了手，伤的是左手还是右手，对你的生活影响度是完全不同的。

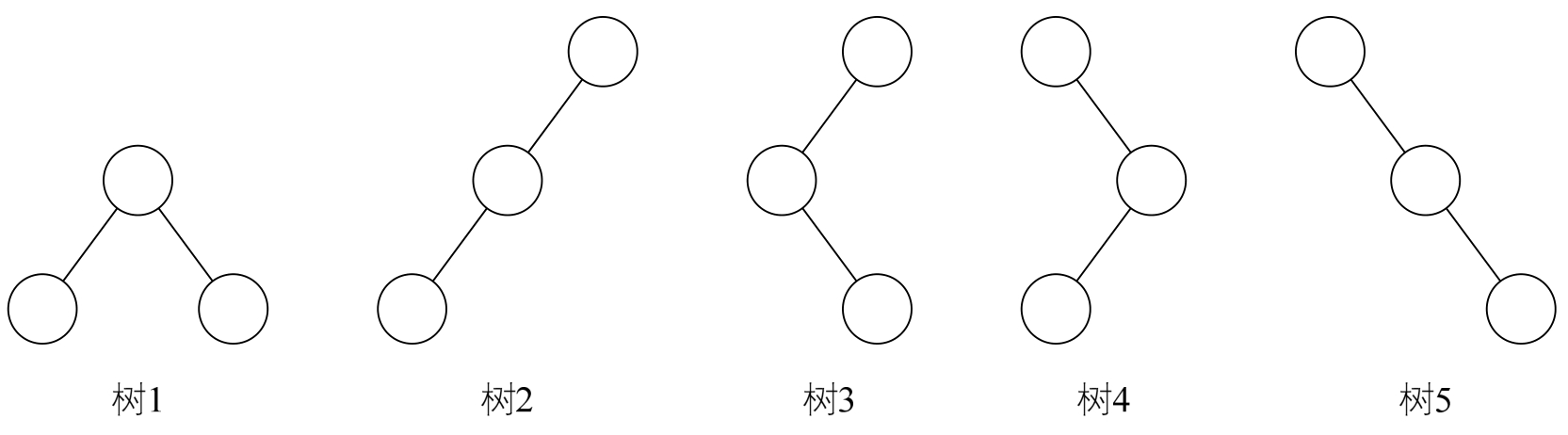
二叉树具有五种基本形态：

1．空二叉树。

2．只有一个根结点。

3．根结点只有左子树。

4．根结点只有右子树。

5．根结点既有左子树又有右子树。

应该说这五种形态还是比较好理解的，那我现在问大家，如果是有三个结点的树，有几种形态？如果是有三个结点的二叉树，考虑一下，又有几种形态？

若只从形态上考虑，三个结点的树只有两种情况，那就是图中有两层的树1和有三层的后四种的任意一种，但对于二叉树来说，由于要区分左右，所以就演变成五种形态，树2、树3、树4和树5分别代表不同的二叉树。

特殊二叉树

我们再来介绍一些特殊的二叉树。这些树可能暂时你不能理解它有什么用处，但先了解一下，以后会提到它们的实际用途。

斜树

所有的结点都只有左子树的二叉树叫左斜树。所有结点都是只有右子树的二叉树叫右斜树。这两者统称为斜树。

上图中的树2就是左斜树，树5就是右斜树。斜树有很明显的特点，就是每一层都只有一个结点，结点的个数与二叉树的深度相同。

有人会想，这也能叫树呀，与我们的线性表结构不是一样吗。对的，其实线性表结构就可以理解为是树的一种极其特殊的表现形式。

满二叉树

在一棵二叉树中，如果所有分支结点都存在左子树和右子树，并且所有叶子都在同一层上，这样的二叉树称为满二叉树。

如图所示就是一棵满二叉树，从样子上看就感觉它很完美。

单是每个结点都存在左右子树，不能算是满二叉树，还必须要所有的叶子都在同一层上，这就做到了整棵树的平衡。因此，满二叉树的特点有：

（1）叶子只能出现在最下一层。出现在其他层就不可能达成平衡。

（2）非叶子结点的度一定是2。否则就是“缺胳膊少腿”了。

（3）在同样深度的二叉树中，满二叉树的结点个数最多，叶子数最多。

完全二叉树

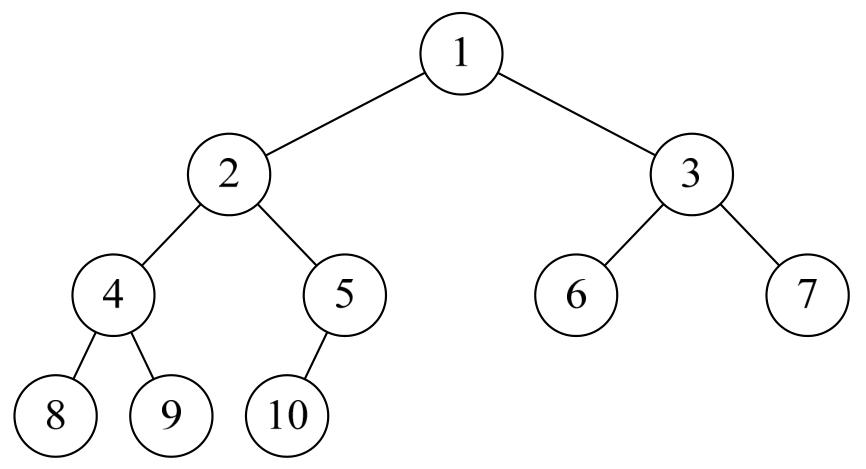
对一棵具有n个结点的二叉树按层序编号，如果编号为i（1≤i≤n）的结点与同样深度的满二叉树中编号为i的结点在二叉树中位置完全相同，则这棵二叉树称为完全二叉树。

这是一种有些理解难度的特殊二叉树。

首先从字面上要区分，​“完全”和“满”的差异，满二叉树一定是一棵完全二叉树，但完全二叉树不一定是满的。
其次，完全二叉树的所有结点与同样深度的满二叉树，它们按层序编号相同的结点，是一一对应的。这里有个关键词是按层序编号：
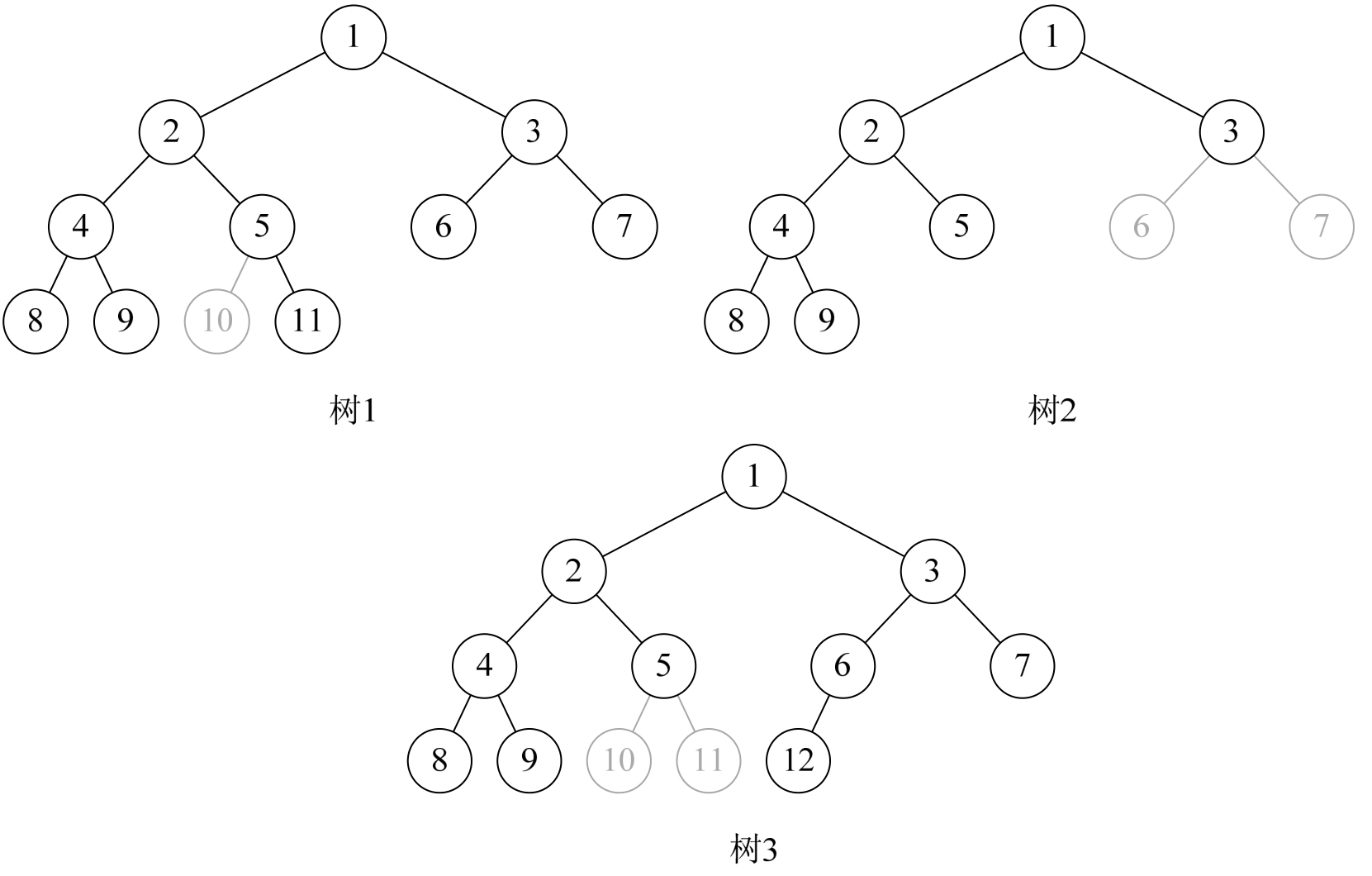
图中的树1，因为5结点没有左子树，却有右子树，那就使得按层序编号的第10个编号空档了。
图中的树2，由于3结点没有子树，所以使得6、7编号的位置空档了。
图中的树3又是因为5编号下没有子树造成第10和第11位置空档。
而上一张图中的树，尽管它不是满二叉树，但是编号是连续的，所以它是完全二叉树。

从这里我也可以得出一些完全二叉树的特点：

（1）叶子结点只能出现在最下两层。

（2）最下层的叶子一定集中在左部连续位置。

（3）倒数二层，若有叶子结点，一定都在右部连续位置。

（4）如果结点度为1，则该结点只有左孩子，即不存在只有右子树的情况。

（5）同样结点数的二叉树，完全二叉树的深度最小。

从上面的例子，也给了我们一个判断某二叉树是否是完全二叉树的办法，那就是看着树的示意图，心中默默给每个结点按照满二叉树的结构逐层顺序编号，如果编号出现空档，就说明不是完全二叉树，否则就是。