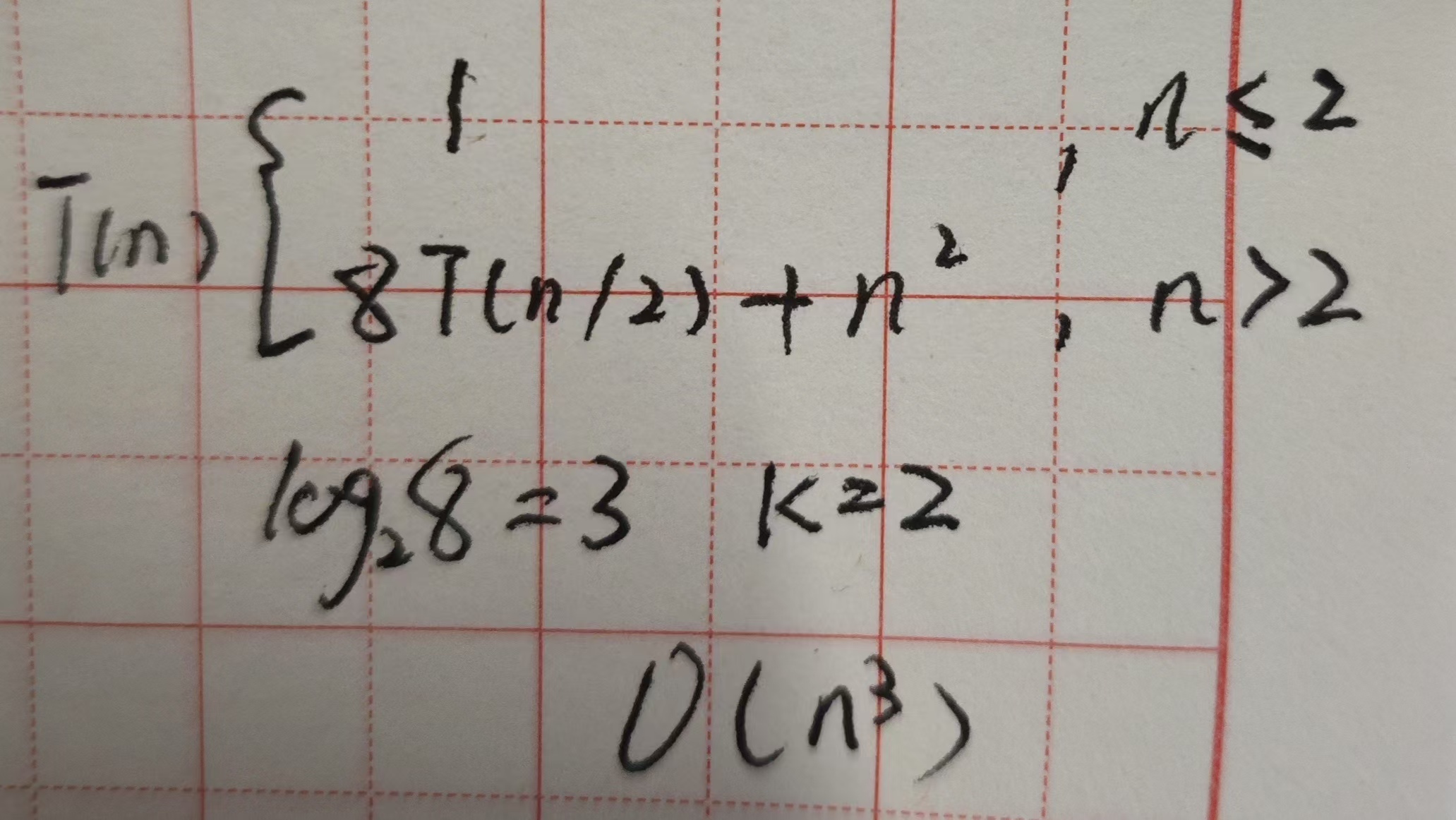算法-堆、排序算法、矩阵乘法
满二叉树、完全二叉树
二叉树遵循下面的规律,当前节点i(但是其实就是逐级填充):
- 左节点为 ix2
- 右节点为 i*2+1
- 父节点为 [i/2] 向下取整
使用数组表示二叉树:
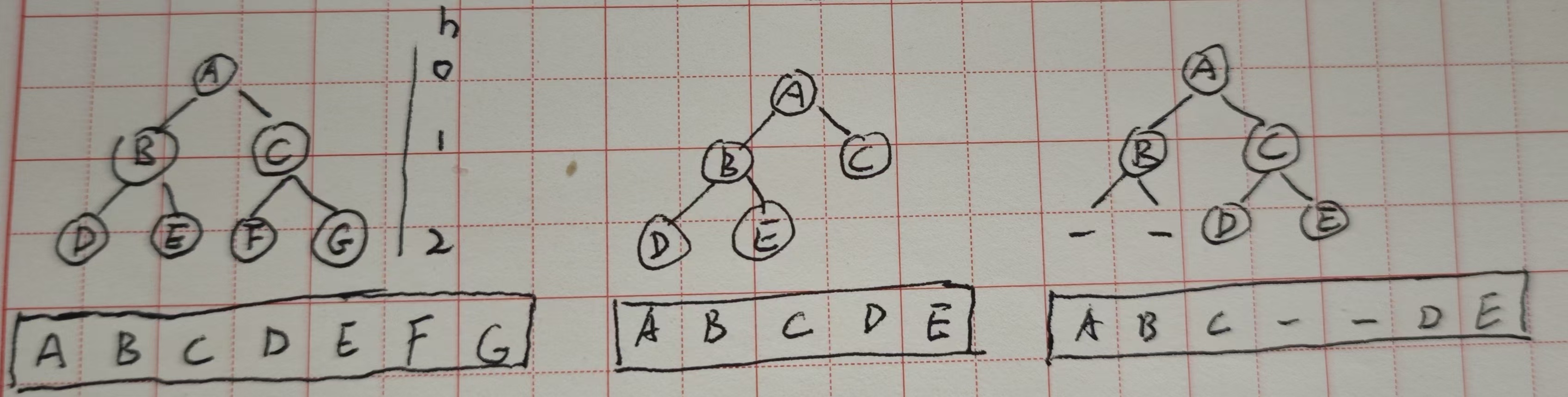
(二叉树的深度自上而下,高度自下而上)(至于高度深度是0,还是1开始只是一个表示不重要)
- 满二叉树(完美二叉树):深度为h,且节点有2(h+1)-1。节点数最大。
- 完全二叉树:看上面数组的表示,前两个为完全,最后一个非完全,因为缺失元素了。
判断是不是完全二叉树:
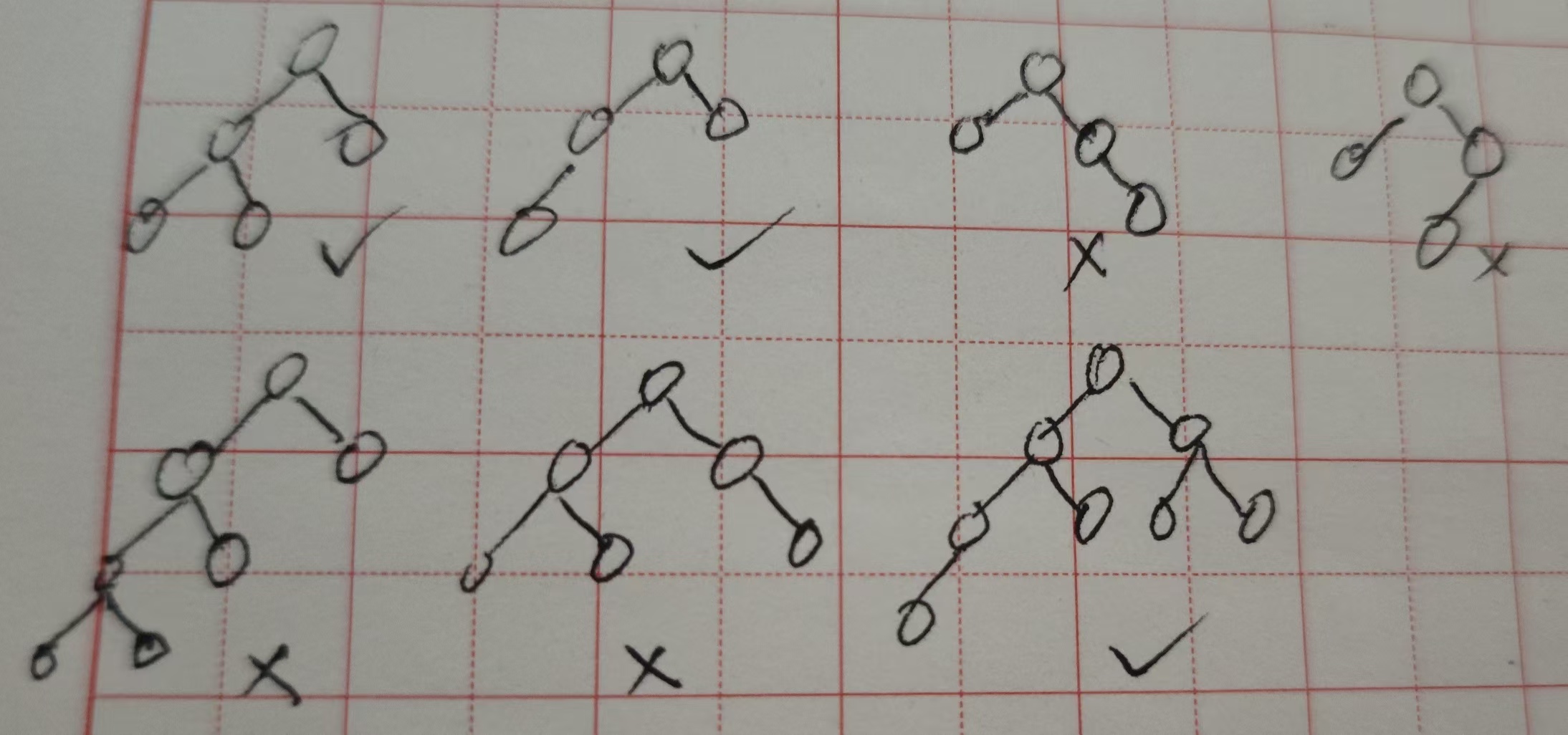
堆
堆是完全二叉树!!
最大堆:父节点要大于或等于后面所有子节点。
最小堆:父节点要小于或等于后面所有子节点。
最大堆的插入、删除
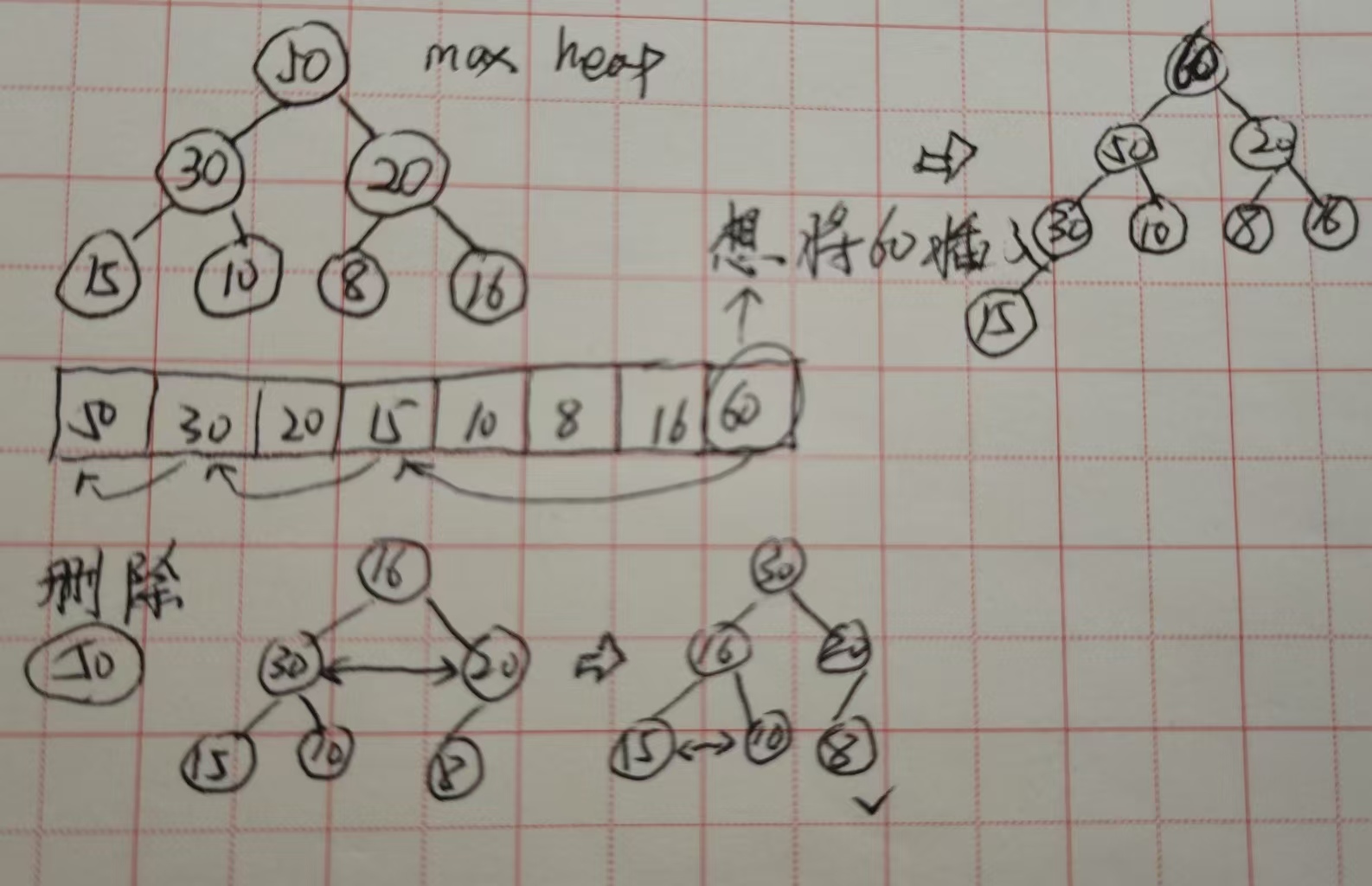
最大堆的插入:
- 60首先插入最后的叶子节点,与父节点比较,比父节点大则交换位置,直到到达正确的位置。
- 时间复杂度就是交换的次数:例子是3次即树深logn。堆插入的时间复杂度O(1)~O(logn)。
最大堆的删除:
- 假如去水果店买苹果,苹果像金字塔一样排列,最好的苹果在金字塔的尖上。那我们最大堆的最大元素在根节点,只能移除根节点即50。移除根元素后不能随意的让30往上顶,这样就不满足完全二叉树。
- 正确做法:将最后的叶子节点挪到根节点,然后子节点相互比较,最大值与父节点比较并交换,直到满足最大堆的条件。堆删除时间复杂度O(logn)。
- 若删除中间元素,首先要遍历找到要删除的元素(n),跟末尾元素交换并删除,后再调整log(n)。由于二叉堆无顺,查找要消耗O(n),一般不推荐使用二叉堆进行查找。
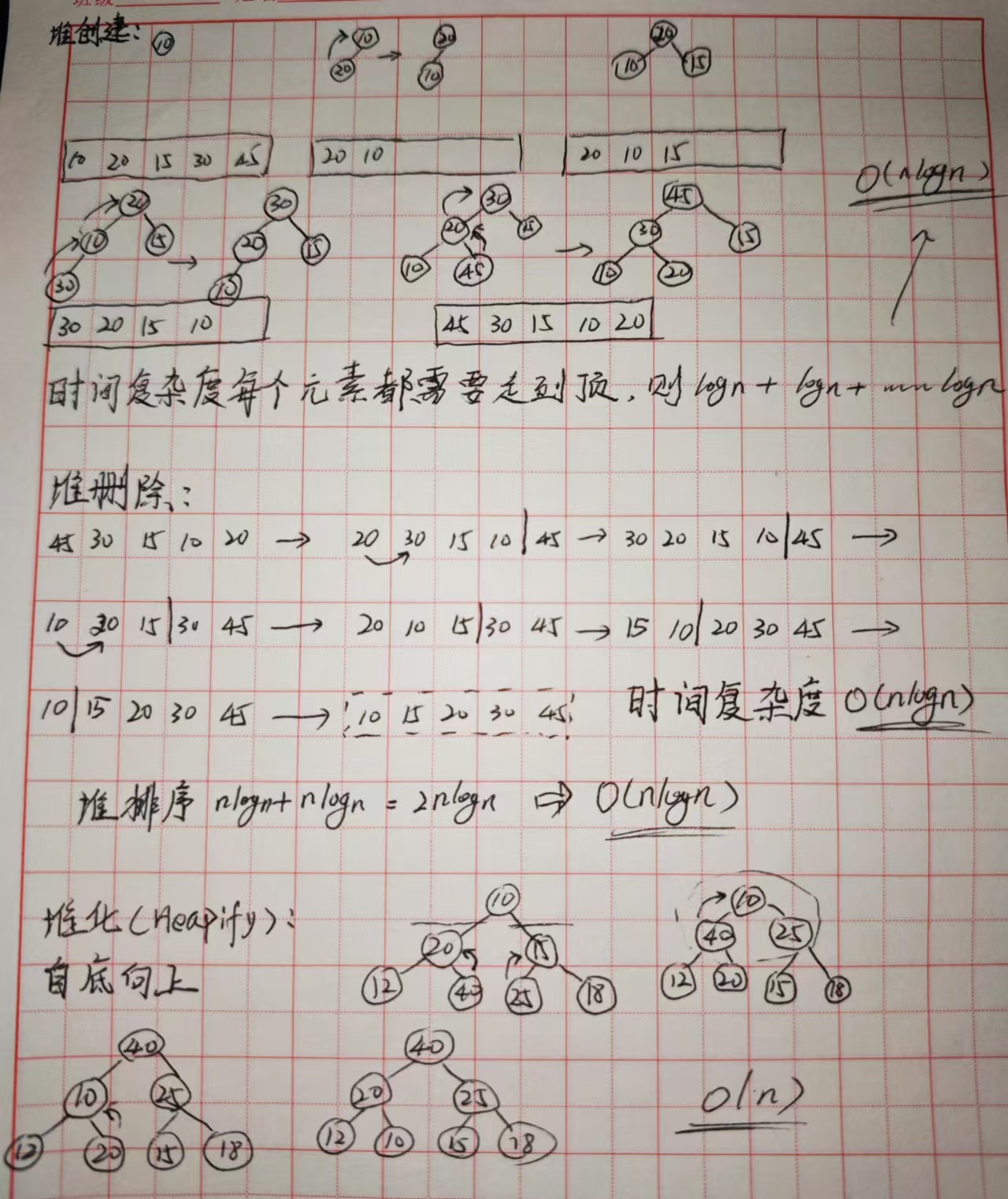
堆创建、堆排序
由上堆删除可知:删除所有元素,并将元素放到删除后的空闲位置,就会发现数组已排序。
堆排序的时间复杂度是O(nlogn)、O(n)
优先级队列
数字本身就有优先级:
- 数字大的优先级更高,那就使用最大堆进行分析
- 数字小的优先级更高,那就使用最小堆进行分析(删除和插入)
这将是最好的数据结构,否则需要的可能是O(n),而现在是O(logn)。
归并排序
合并:两个及以上有序列表合并成一个有序列表的过程。
2-way merge sort
1.例子:有两个有序列表A,B,合成列表C

merge(A,B,m,n){i=1;j=1;k=1;while(i<=n && j<=m){if(A[i]<=B[j]){C[k]=A[i];k++;i++;}else{C[k]=B[j];k++;j++;}}for(;j<=m;j++){C[k]=B[j];k++;}
}
时间复杂度O(m+n)
2.M路合并:多个列表合并。采取的就是两两合并(2-way merge sort),可以任意两个如下:
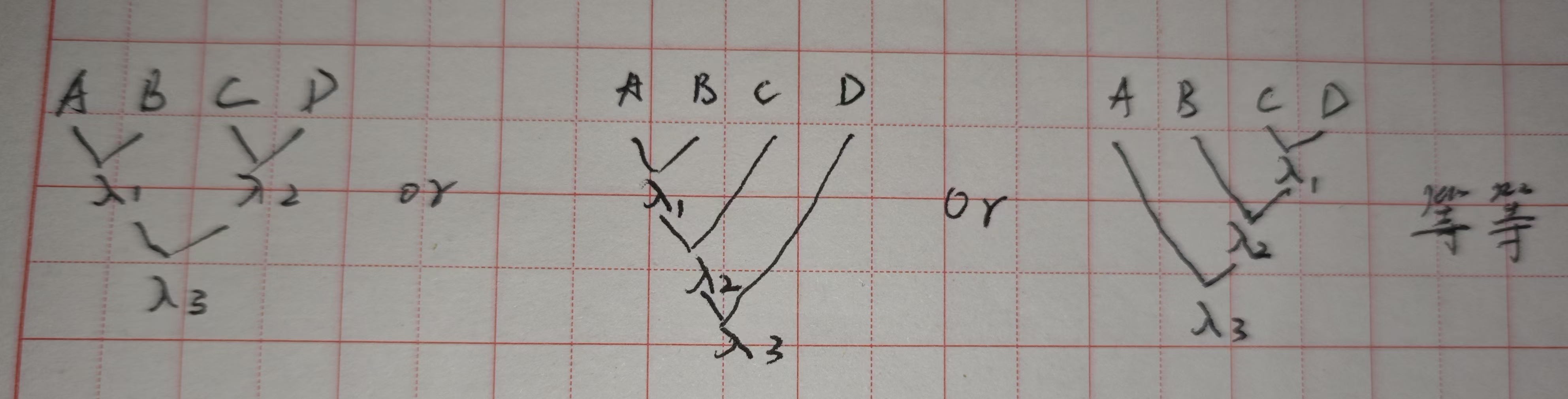

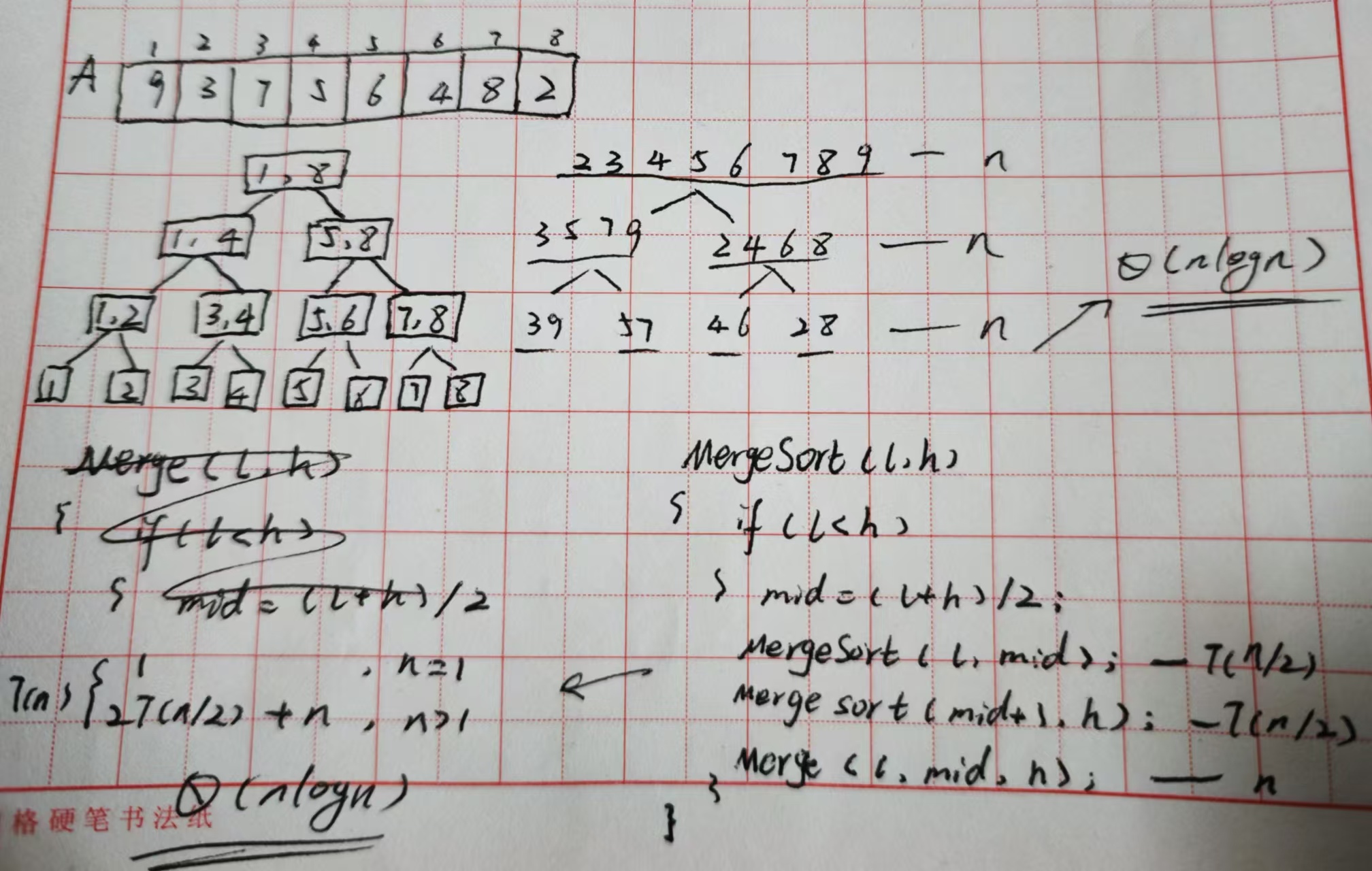
merge sort
分而治之思想,先拆分后合并
优缺点
优点:
-
适合大列表
-
适合链表(可以在不创建新链表的情况下进行排序)
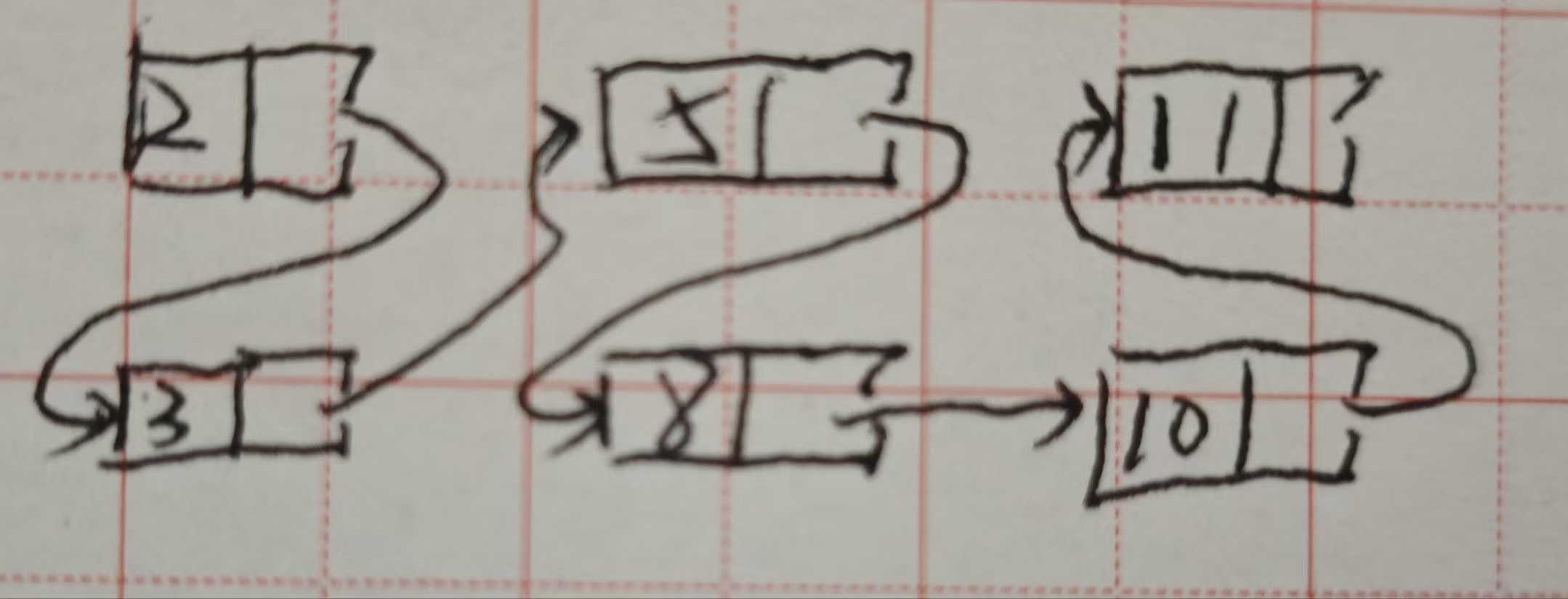
-
外部排序(每次带入一部分元素块进入主内存,主内存就不需要那么大空间)
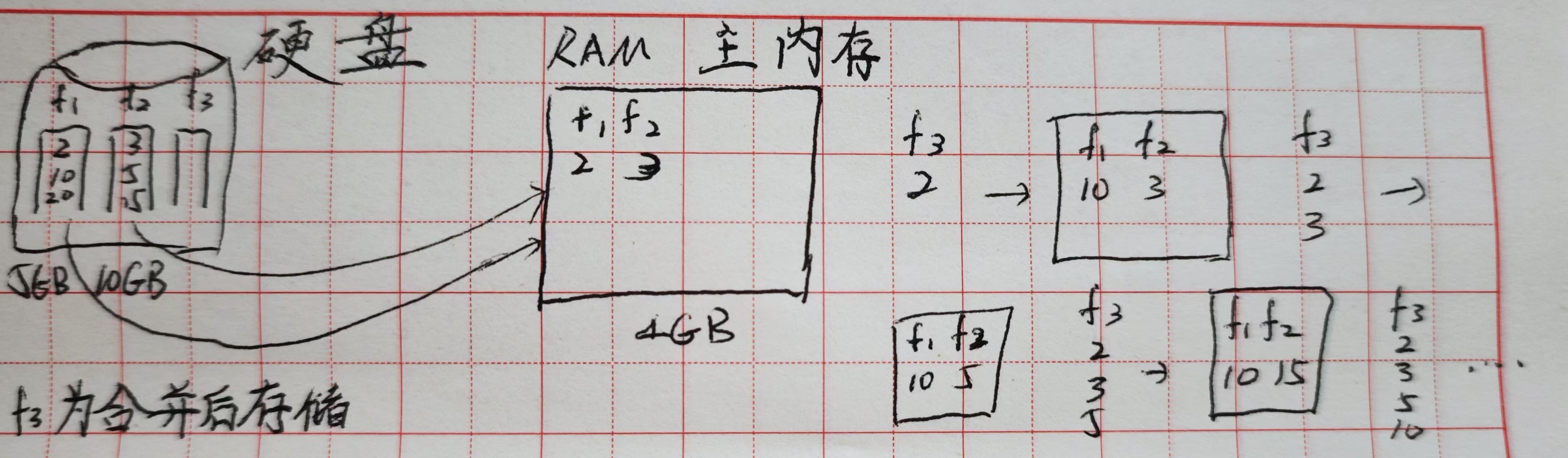
-
稳定(同样的数字保持原来的顺序)
缺点:
- 数组进行排序,需要额外的空间
- 不适合小问题(元素很少,不需要拆分,那么会在递归上浪费时间。借用插入排序来得到结果)
- 递归(会使用内存的堆栈,需要的堆栈空间=树高logn,再加上第一点的额外空间O(n+logn)渐进O(n))
快速排序
举例
遵循分而治之。
分区位置:某一元素左边的元素都比他小,右边都比他大,那么他就处于排序位置。
分区算法:找到分区位置,i是直到找到比核心更大的,j是直到找到比核心更小的,交换位置。过程如下:

//分区算法
partition(l,h){pivot=A[l];i=l;j=h;while(i<j){do{i++;}while(A[i]<=pivot);do{j--;}while(A[i]>pivot);swap(A[i],A[j]);}swap(A[l],A[j]);return j;
}//快速排序
QuickSort(l,h){if(l<h){j=partition(l,h);QuickSort(l,j-1);QuickSort(j+1,h);}
}
分析时间复杂度
best case-----O(nlogn) 分区后j一直取中间(这种情况很难遇见)
worst case—O(n2)
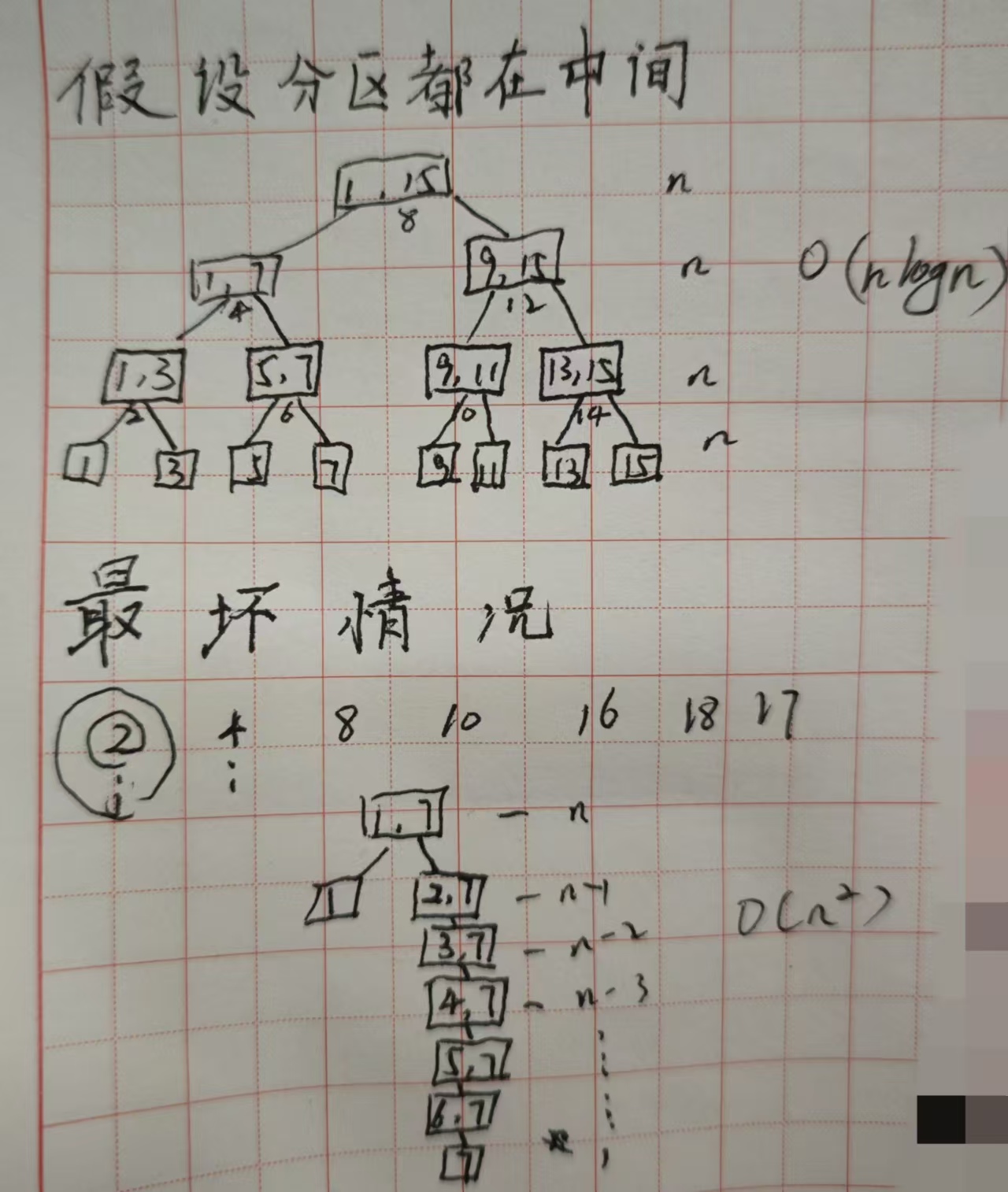
为了避免最坏情况可以一直选择中间作为核心元素,或随机选择核心元素
快速排序用了递归,占用堆栈空间logn 到 n(树高)
矩阵乘法
1.使用简单方法,三个循环,O(n3)
2.采用分而治之,最小单位就是小于等于2x2的矩阵,直接就用公式不用循环,公式的话是4行,可以说时间常数就是O(4)。
3.不满足的矩阵可以补0成为4x4,8x8等等的矩阵,然后采取分而治之。
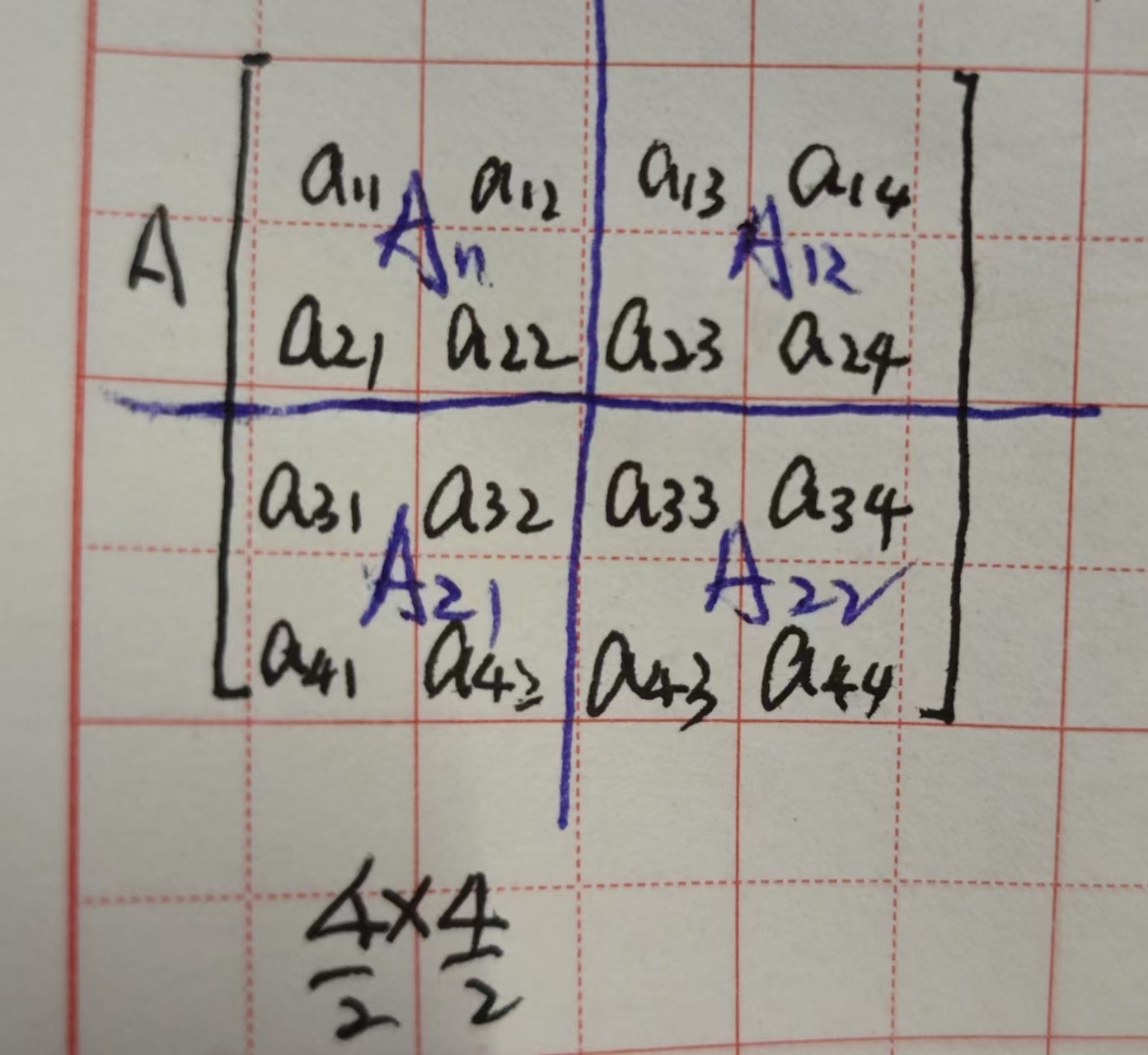
mm(A,B,n){if(n<=2){c=4 formulas;}esle{//拆分再合并mid=n/2;mm(A11,B11,mid)+mm(A12,B21,mid);mm(A11,B12,mid)+mm(A12,B22,mid);mm(A21,B11,mid)+mm(A22,B21,mid);mm(A21,B12,mid)+mm(A22,B22,mid);}
}
分治算法的矩阵乘法也是O(n3),采用了递归还会额外占用堆栈