小杰机器学习（two）——导数、损失函数、斜率极值最值、微分规则、切平面与偏导数、梯度。
1.求导法则
（1）在机器学习中微积分的作用
在机器学习和深度学习中，需要衡量预测的结果和实际结果的一个差异，使用一个叫损失函数的数学打分器比对。损失函数越小，表示结果预测的准；损失函数越大表示结果预测的不准。
比如，如果我们预测明天下雨的概率是80%，但实际上明天是晴天，那么我们的预测就不准，损失函数的值就会比较高。反之，如果我们预测明天下雨的概率是5%，而明天确实是晴天，虽然我们还是预测错了，但相对来说，我们预测得“更接近”实际情况，所以损失函数的值就会低一些。
损失函数在机器学习和深度学习中非常重要，因为它指导着模型的学习过程，让模型知道应该如何调整自己的参数，以便更好地预测未来的结果。
在机器学习或者深度学习中，绝大部分任务是构建一个损失函数，然后使其最小化，这个优化的过程就是微分。
以上过程在后面学习的框架中可以自动计算，但是背后的数学原理还是需要简单学习的。
（2）导数
【例子1】小车在马路上匀速前进，一共900m，小车走了30s。
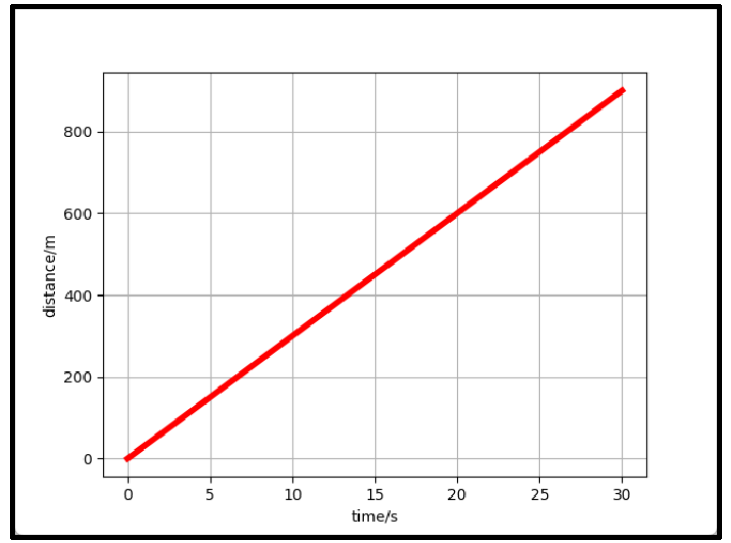
在17.5秒时，小车的速度多快？
答案：900/30=30m/s
【例子2】小车在马路上非匀速前进，一共900m，小车走了30s。
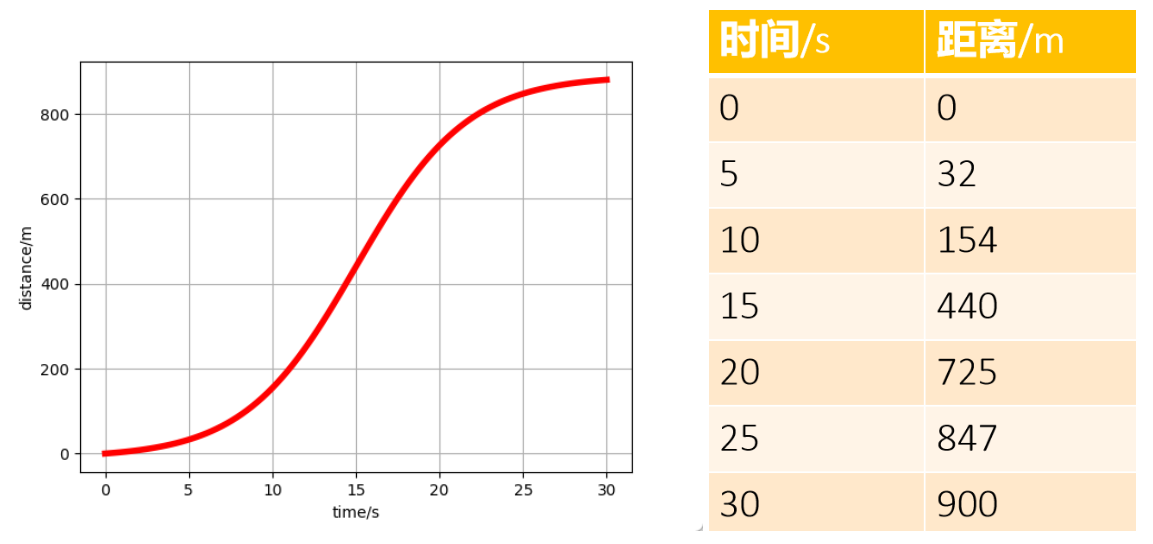
右表表示每间隔5s测一次数据。
在17.5秒时，小车的速度多快？
答案：(725-440)/(20-15) = 57m/s
把多个时间点细分，例如15-20秒，每秒测一次。
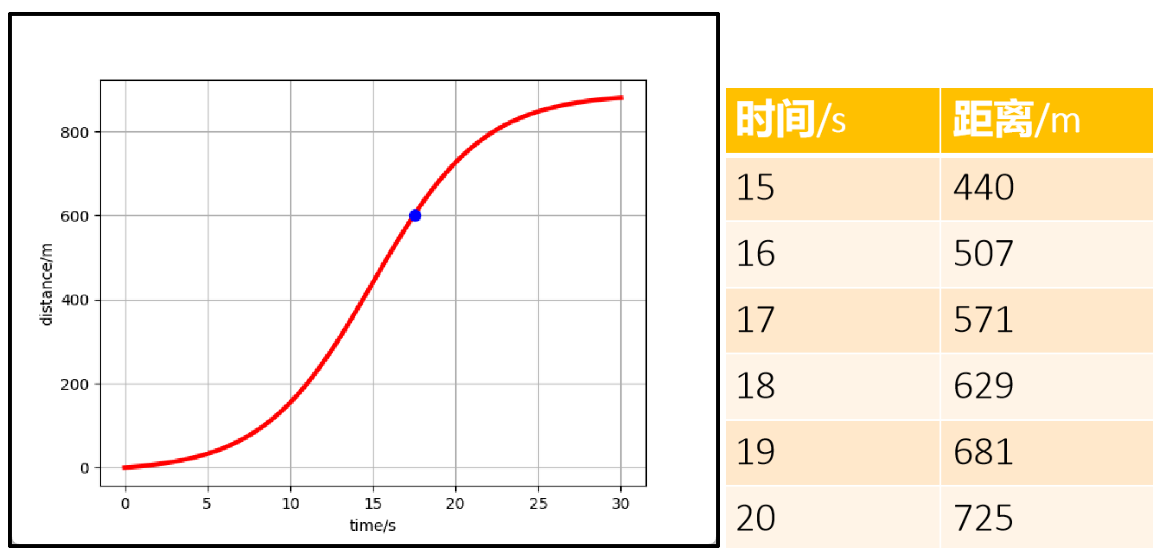
在17.5秒时，小车的速度多快？
答案：(629-571)/(18-17) = 58m/s
通过上面的计算可以得到结论，测速的间隔越小，速度越精准。
此时如果把时间间隔趋向于无穷小，就可以使速度结果无限趋向于真实值。
速度的值，实际上就是所在点的切线斜率。
速度 = 瞬时变化率
拉格朗日表示法：
莱布尼茨表示法：
导数是函数，如果把上图中每个点的斜率都用一个函数表示，这个函数就是“导函数”，通常叫为“导数”。
导函数表示的切线集合可以描述：
- 函数的整体变化趋势
- 也可以表示部分的变化趋势
- 还可以表示某个点的变化趋势
（3） 斜率的极值和最值
【例子】还是刚才的小车，但是小车学会了倒车。
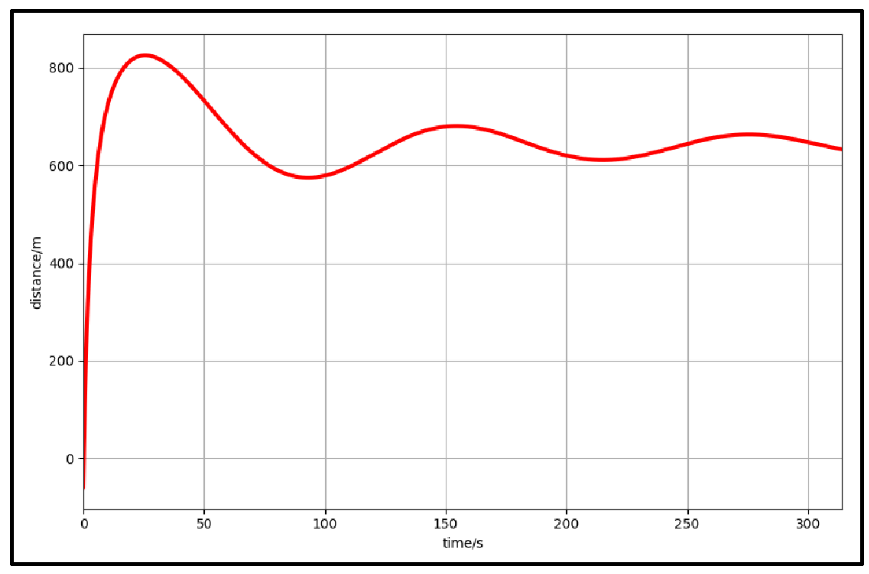
Q1：哪里的速度为0？
A1：斜率为0的点表示速度为0。
Q2：哪里的距离起点最近/最远？
A2：最远或最近的点斜率都为0。
如果上面的图像是损失函数，那么斜率为0的点可能就是损失函数最小值或最大值。
极小值/极大值：局部范围的极值。
最小值/最大值：全局的极值。
这些内容是以后机器学习梯度下降的重要思想。
（4）常见的导数
① 常数
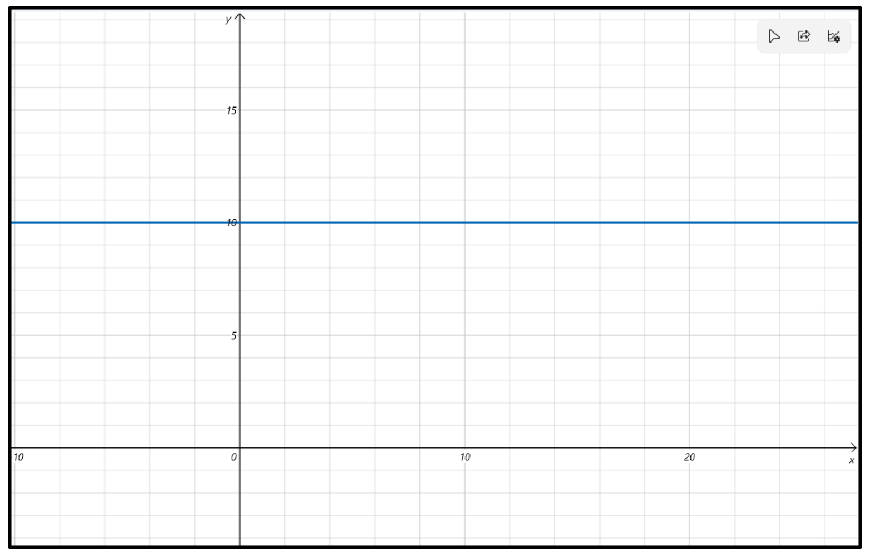
结论：
② 线性函数
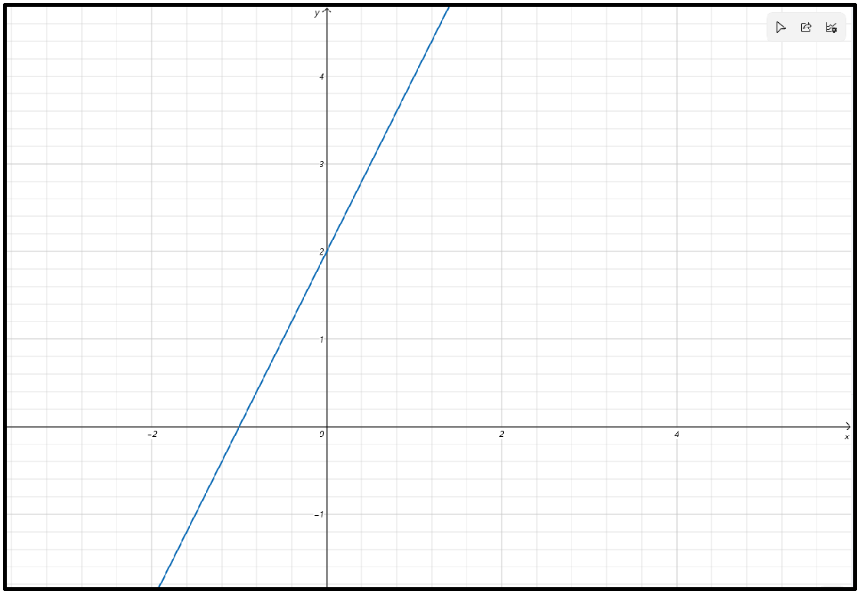
结论：
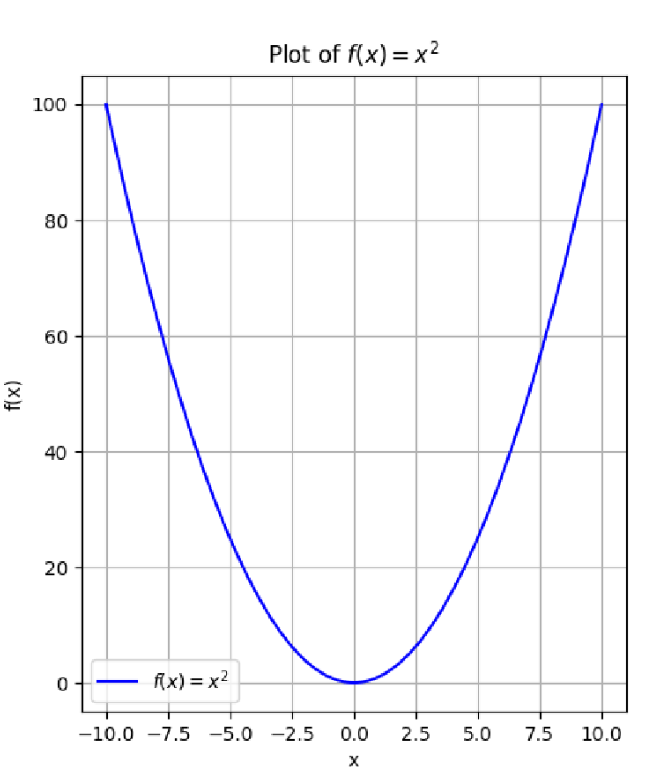
③ 二次方程
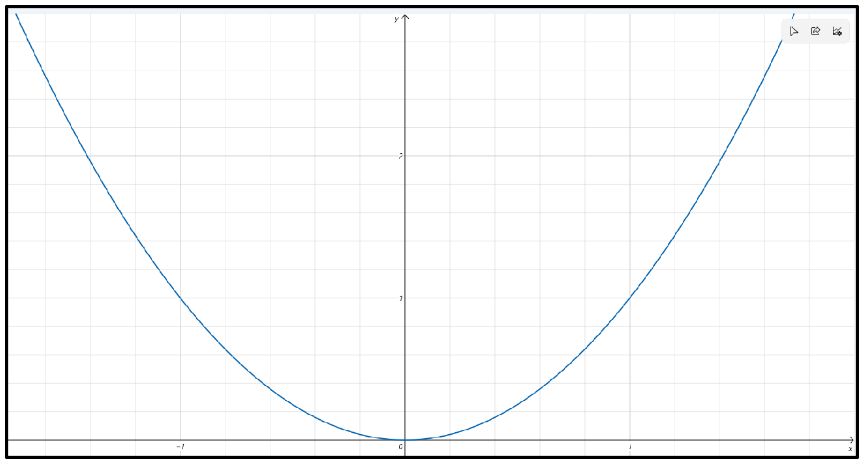
结论：
④ 其他函数
⑤不可微函数
如果一个点存在导数，那么该点的函数会被该点微分。也就是说如果要使函数在整个区间内保持微分，则表示区间中每个点都必须存在导数。
实际上，并不是所有的函数在每个点都能找到导数，这样的函数就是不可微函数，例如：
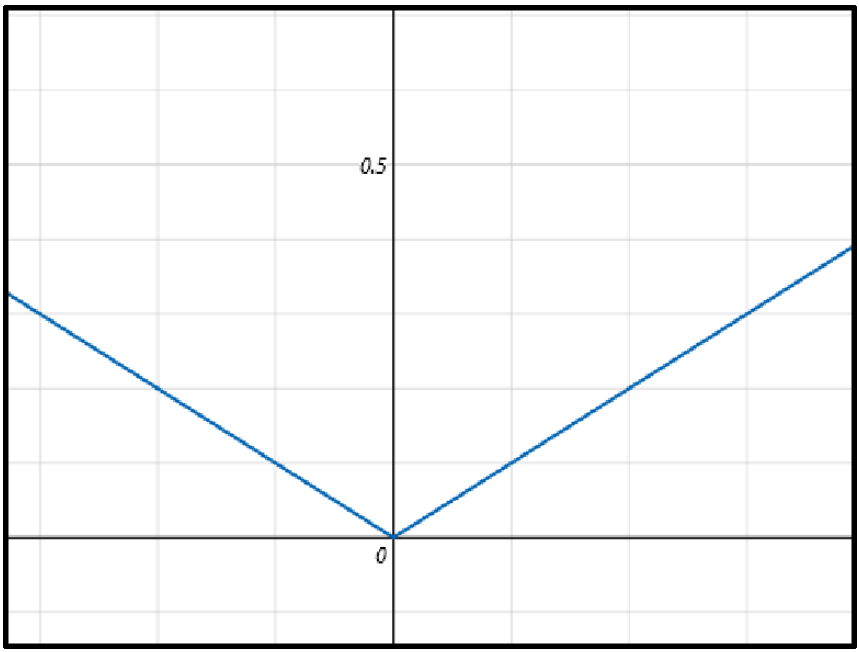
在(0,0)点有无数个切线，所以此点不能求导，这个函数就是不可微函数。
再例如
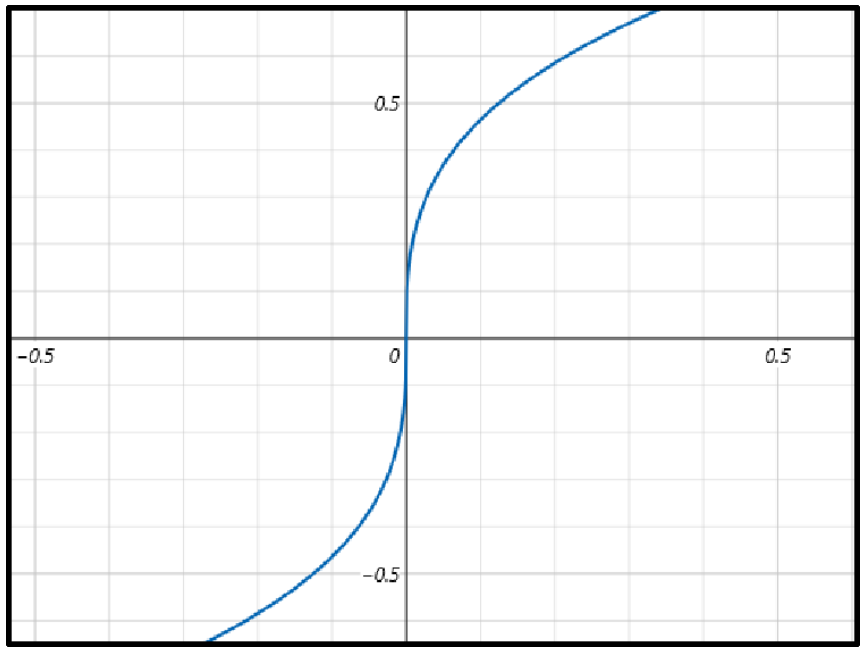
在(0,0)点切线与y轴重合，表示无穷大，无法求导，此函数也是不可微函数。
（5）导数的性质（微分规则）
①乘以标量
已知
，那么的导数是多少？
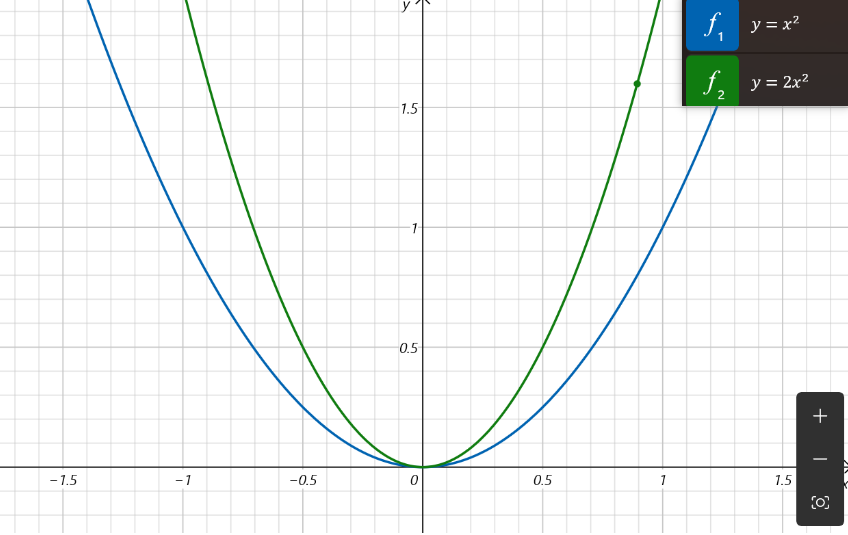
答案：
② 加和法则
绿色为人在船上奔跑的时间和距离，蓝色为船离开码头的时间和距离，红色为人相对码头的时间和距离。
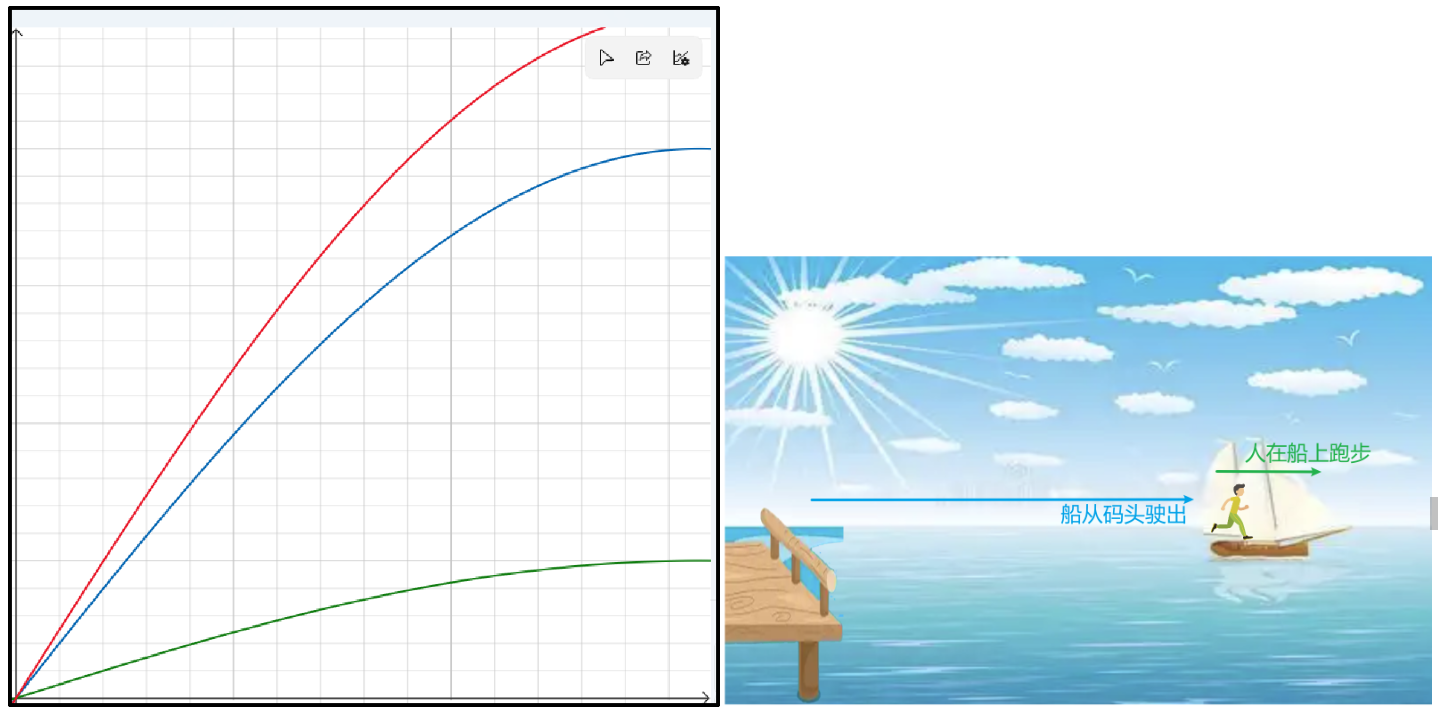
结论：
人距离码头的距离 = 船离开码头的距离+人奔跑的距离
人相对码头的速度 = 船相对码头的速度+人相对于船的速度
③乘法法则
第一个函数是g(x)，第二个函数是h(x)，f(x)=g(x)h(x)，求f'(x)
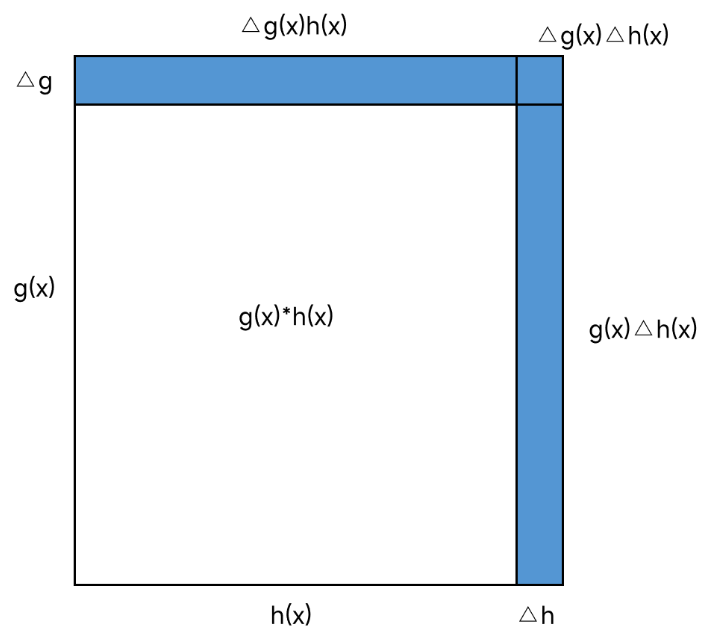
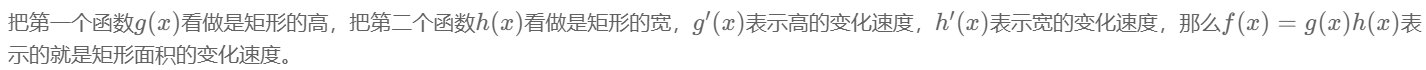
答案：
④ 链式法则
链式法则（Chain Rule）是微积分中用于求复合函数导数的一个基本法则。如果你有一个复合函数，比如，其中y 是 x的函数，g(x)是内函数，f是外函数，那么链式法则允许你分别求出外函数和内函数的导数，然后将它们相乘来求复合函数的导数。
具体来说，链式法则可以表述为：
这里的是外函数f对内函数g(x)的导数，而是内函数g(x)对自变量x的导数。
【例子】
假设有一个复合函数
，求这个函数对x的导数？
解：
1. 确定内函数和外函数
内函数：
外函数：
2. 分别求导
外函数对内函数的导数：
内函数对x的导数：
3. 应用链式法则
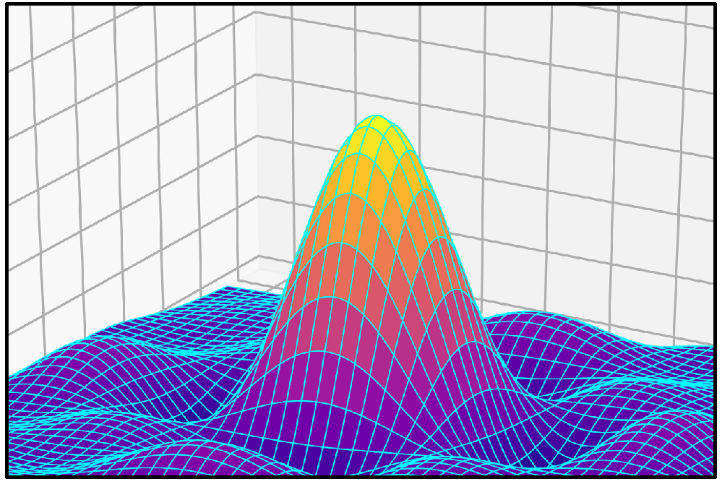
（6） 切平面与偏导数
①输入和输出的数量
之前函数都是一个输入和输出，现在可以拓展到两个输入和一个输出。
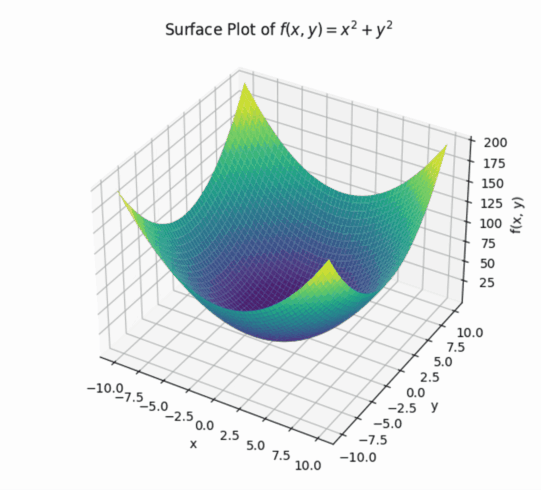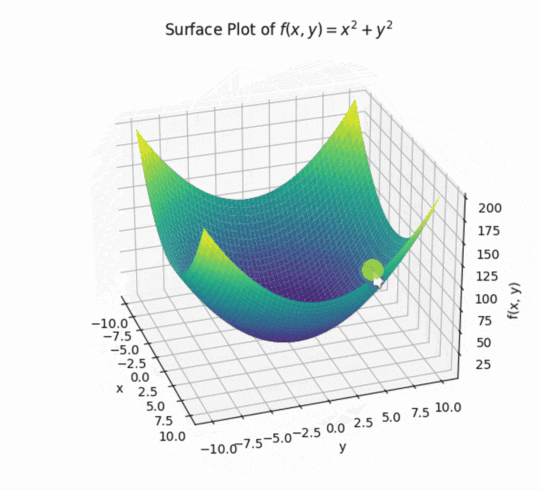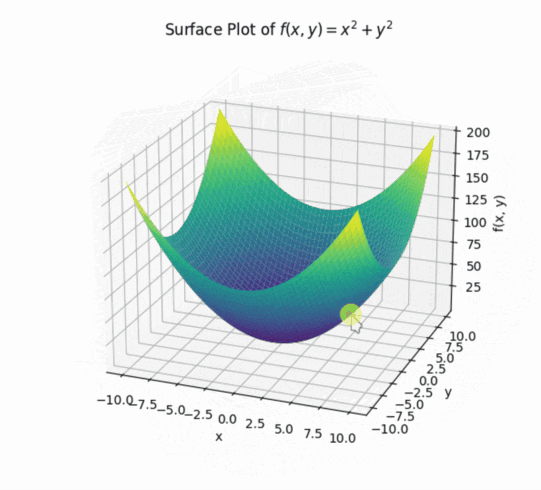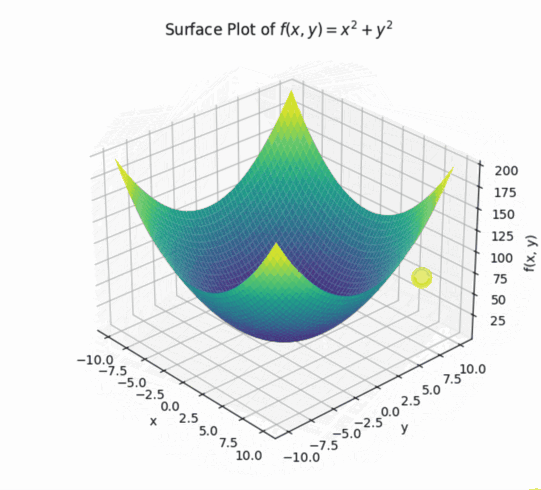
②偏导数
如果把输入的x和y其中一个看做是常数，此时导数就相当于之前的平面导数了，即一个输入的导数。
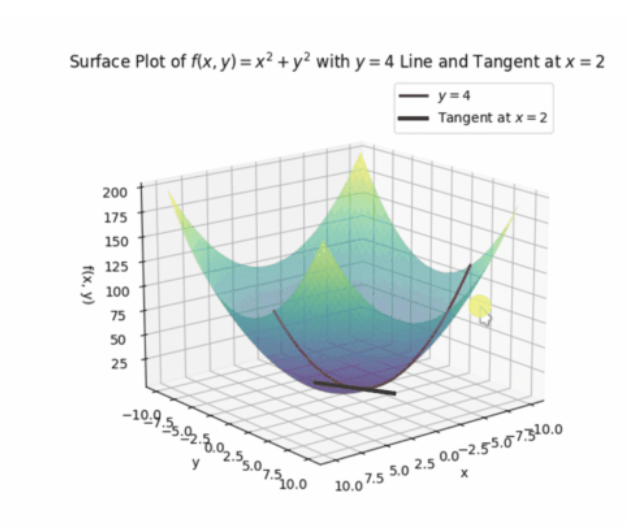
例如当y=4时，可以求出上图中的曲线的偏导数：
以上过程就是求偏导的过程，同样也可以让x等于常数，同样可以求偏导。
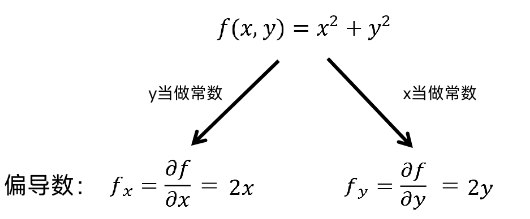
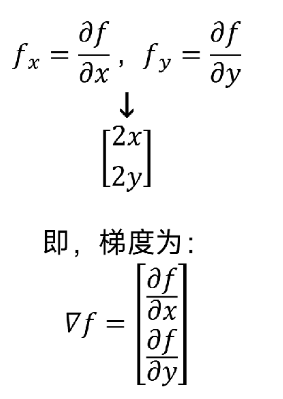
（8）梯度
可以认为梯度是偏导数的集合。
以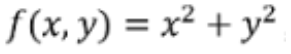
为例，说明梯度的概念。
