25高教社杯数模国赛【B题高质量成品论文+无盲点解析】第一弹

注：本内容由”数模加油站“ 原创出品，虽无偿分享，但创作不易。

欢迎参考teach，但请勿抄袭、盗卖或商用。

四、 双光束干涉框架下碳化硅外延层厚度的光学建模与解析反演
4.1 问题一模型建立与求解
问题一限定仅考虑外延层上表面与外延层—衬底界面各一次作用形成的干涉。为与该物理边界严格对齐，采用两束叠加框架：将非偏振入射在两条光路上的复振幅相干叠加，反射率写为

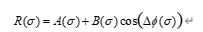
其中相位函数 $\Delta \varphi (\sigma )$ 以线性因子的形式嵌入厚度 ，从而把“可观测的条纹结构”与“待求的几何厚度”建立一一对应。
该选择的充分性体现在三方面：其一，与题意约束完全一致；其二，$\frac{\mathrm{d}\Delta \varphi }{\mathrm{d}\sigma }$ 对 $d$ 呈线性比例，保证单参数可识别；其三，模型自由度低而结构强，便于通过极值差分、全谱相位回归与直接谱拟合三条等价路径实现求解，并在同一框架内完成回代重构与残差谱等自洽性检验。

4.2 两束叠加下的光学场表达与反射率构成
考虑非偏振入射在上表面（介质 $0!\to !1$）与下界面（介质 $1!\to !2$）的作用。对任一偏振分量（$s$ 或 $p$），上表面反射的复振幅为 ，透入外延层、在下界面反射并往返一次后从上表面透出的复振幅为：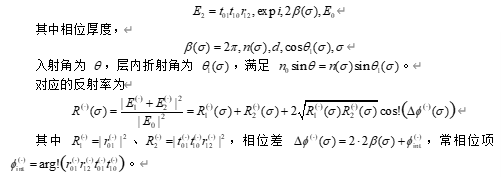
非偏振光取两偏振分量算术平均得到 $R(\sigma )=\frac{1}{2}(R^{(s)}(\sigma )+R^{(p)}(\sigma ))$。将缓慢变化的项收集为 $A(\sigma )$ 与 $B(\sigma )$，可统一写成 $R(\sigma )=A(\sigma )+B(\sigma )\cos !(\Delta \varphi (\sigma ))$，其中厚度信息仅进入 $\Delta \varphi (\sigma )$。为后续简洁，记 $\Delta \varphi (\sigma )=4\pi ,n(\sigma ),d,\cos {\theta }_1(\sigma ),\sigma +{\varphi }_{\mathrm{int}}$。
在完成两束光学场的相干表述后，接下来把谱纹的可观测结构转化为对厚度的稳定信息载体，关键在于相位函数对波数的梯度刻画与条纹密度的微分关系。
为便于将上式中的慢变项与条纹结构与实测数据对齐，采用数据驱动的方式从测得反射谱中提取“慢变基线”与“包络”，其中前者对应 $A(\sigma )$ 的平滑近似，后者对应 $B(\sigma )$ 的平滑近似；二者仅通过宽窗平滑获得，不涉及任何物理拟合或参数估计。该可视化用于验证：在本数据带宽内，反射谱可被分解为“缓慢起伏的背景”与“随波数发生相位调制的条纹”两部分，与两束叠加模型的构成保持一致（见图1）。

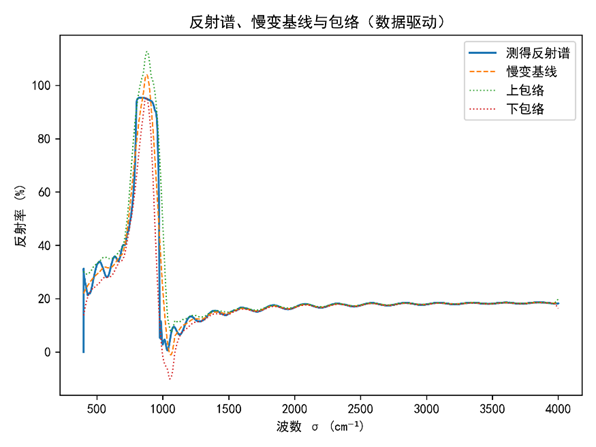
实线为实测反射谱 $R_{\text{meas}}(\sigma )$；虚线为宽窗平滑得到的慢变基线 $\hat{A}(\sigma )$；点划线为上、下包络 $\hat{A}(\sigma )\pm \hat{B}(\sigma )$，其中 $\hat{B}(\sigma )$ 为解析信号包络的平滑近似。该图仅展示数据的结构性特征，不进行参数拟合与数值求解。
从图中可以观察到：（i）在低波数段出现宽幅的反射峰谷结构，随后进入较宽的条纹区，条纹的间距与对比度随波数缓慢变化；（ii）慢变基线 $\hat{A}(\sigma )$ 在全带内起伏平缓，表明背景项可以视为缓慢项；（iii）包络 $\hat{B}(\sigma )$ 的变化同样远慢于条纹相位的变化，说明条纹主要由相位项 $\Delta \varphi (\sigma )$ 驱动，而幅值项仅起缓慢调制作用。上述特征与两束叠加的模型结构一致：$R(\sigma )$ 可视为“慢变项 $A(\sigma )$ 与 $B(\sigma )$”叠加“相位调制的余弦项”。本图只基于数据变换得到，不涉及厚度或折射率的数值求解，也不比较不同模型。
在确认两束叠加模型能够以“慢变背景 + 相位调制条纹”的形式刻画实测谱形之后，下一节转向对相位函数随波数的变化率进行刻画。由 $\Delta \varphi (\sigma )=4\pi ,n(\sigma ),d,\cos {\theta }_1(\sigma ),\sigma +{\varphi }_{\mathrm{int}}$ 可得相位—波数梯度 $\frac{\mathrm{d}\Delta \varphi }{\mathrm{d}\sigma }$，进而建立条纹密度与厚度之间的微分联系，为后续的解析反演与全谱回归奠定基础。

4.3 相位—波数梯度与条纹密度的微分联系
定义 $G(\sigma )=n(\sigma )\cos {\theta }_1(\sigma )$。
由，
$\Delta \varphi (\sigma )=4\pi ,d,G(\sigma ),\sigma +{\varphi }_{\mathrm{int}}$
可得相位梯度，

当色散弱（$n^{\prime }(\sigma )\approx 0$）时退化为常用形式 $\Delta \sigma \approx \frac{1}{2,n(\bar{\sigma }),d,\cos {\theta }_1(\bar{\sigma })}$。该结果以微分方式连接“条纹密度—厚度”，为解析反演与全谱回归提供统一的理论基础。
在获得条纹密度与相位梯度后，以下给出基于极值条件的解析反演式，并在一般色散情形下给出一阶修正表达，使厚度求解具备封闭形式与可核验性。

4.4 厚度的解析反演：极值差分与一阶色散修正谱极大/极小满足，
$\Delta \varphi ({\sigma }_m)=2\pi m$ 或 $\Delta \varphi ({\sigma }_m)=(2m+1)\pi$，$m\in \mathbb{Z}$
对相邻极值 ${\sigma }_m,{\sigma }_{m+\Delta m}$，由，
$\Delta \varphi (\sigma )=4\pi ,d,G(\sigma ),\sigma +{\varphi }_{\mathrm{int}}$
得，
$4\pi ,d,[,G({\sigma }_{m+\Delta m}),{\sigma }_{m+\Delta m}-G({\sigma }_m),{\sigma }_m,]=2\pi ,\Delta m$
从而得到厚度差分反演，
$d=\frac{\Delta m}{2,[,G({\sigma }_{m+\Delta m}),{\sigma }_{m+\Delta m}-G({\sigma }_m),{\sigma }_m,]}.$
若取 $\bar{\sigma }=({\sigma }_{m+\Delta m}+{\sigma }_m)/2$ 与 $\Delta \sigma ={\sigma }_{m+\Delta m}-{\sigma }_m$，使用一阶泰勒展开.并代入$G^{\prime }(\bar{\sigma })=n^{\prime }(\bar{\sigma })/\cos {\theta }_1(\bar{\sigma })$，得到含色散修正的局部表达，

在实现层面，前者用于精确差分（直接以多个极值对代入求 $d$ 并以稳健统计聚合），后者用于快速核验与初值生成。
解析反演能够在有限谱点上得到封闭解。为更充分利用全部采样点的信息，提高鲁棒性，下一节转向全谱相位的加权回归求解。

4.5 全谱相位提取与加权回归的厚度估计

定义去偏相位，$\phi (\sigma )=\Delta \varphi (\sigma )-{\varphi }_{\mathrm{int}}=4\pi ,d,G(\sigma ),\sigma$。
对极值点集 ${\sigma }_{m_k}$ 有 $\phi ({\sigma }_{m_k})=2\pi m_k$，令 $x_k=G({\sigma }_{m_k}),{\sigma }_{m_k}$、$y_k=m_k$ 则 $y_k=2d,x_k$。在不显式定位极值的全谱框架下，可对测得的反射率 进行宽窗去趋势得到 ，构造解析信号 $Z(\sigma )=R_c(\sigma )+i,\mathcal{H}{R}_c(\sigma )$（$\mathcal{H}\cdot$ 为希尔伯特变换），取瞬时相位 $\varphi (\sigma )=\arg Z(\sigma )$，经相位去缠绕与常相位去除得到 $\hat{\phi }(\sigma )$，并建立线性回归模型 $\hat{\phi }(\sigma )=4\pi ,d,G(\sigma ),\sigma +ϵ(\sigma )$。考虑条纹对比度对相位信噪比的影响，采用权重函数 $w(\sigma )\propto B^2(\sigma )$，得到加权最小二乘估计，$\hat{d}=\frac{{\sum }_{\sigma }w(\sigma ),G(\sigma ),\sigma ,\hat{\phi }(\sigma )}{4\pi ,{\sum }_{\sigma }w(\sigma ),(G(\sigma ),\sigma {)}^2}.$
若同时估计常相位偏置，可引入截距 $\alpha$，解，
${\min }_{d,\alpha }{\sum }_{\sigma }w(\sigma )(\hat{\phi }(\sigma )-4\pi ,d,G(\sigma ),\sigma -\alpha {)}^2$
在经典线性回归假设下，若 $\mathrm{Var}[ϵ(\sigma )]={\sigma }_{\varphi }^2/w(\sigma )$，则方差表达为 $\mathrm{Var}[\hat{d}]=\frac{{\sigma }_{\varphi }^2}{(4\pi {)}^2{\sum }_{\sigma }w(\sigma )(G(\sigma ),\sigma {)}^2}$，为后续可靠性评估提供直接的理论基线。
相位回归以线性结构利用了全谱信息。与之等价，也可直接在反射率域构造误差并最小化，避免显式相位提取；下面给出这一等价求解与对厚度的灵敏度分析。

4.6 直接谱拟合的等价求解与厚度灵敏度
以两束模型表示，
$R_{\mathrm{mod}}(\sigma )=P_A(\sigma )+P_B(\sigma )\cos (4\pi ,d,G(\sigma ),\sigma +{\varphi }_0)$
其中 $P_A(\sigma ),P_B(\sigma )$ 为 $A(\sigma ),B(\sigma )$ 的平滑近似（如样条或大窗口光滑），${\varphi }_0$ 为常相位偏置。令残差 $e(\sigma )=R_{\mathrm{meas}}(\sigma )-R_{\mathrm{mod}}(\sigma )$，最小化 $J(d,{\varphi }_0,P_A,P_B)={\sum }_{\sigma }{e}^2(\sigma )$。对厚度的解析灵敏度为，
$\frac{\partial R_{\mathrm{mod}}}{\partial d}=-P_B(\sigma ),\sin (4\pi ,d,G(\sigma ),\sigma +{\varphi }_0)\cdot 4\pi ,G(\sigma ),\sigma$
据此可在高斯—牛顿或 LM 框架下进行参数更新。为增强稳定性，可采用分块策略：外层迭代在 $d,{\varphi }_0$ 上最小化 $J$，内层以约束光滑更新 $P_A,P_B$（其作用仅在吸收慢变项），在最优点处该分块策略与上一节的加权回归等价。识别性方面，当 $G(\sigma ),\sigma$ 在测量带宽上非退化且单调增长时，相位函数随 $\sigma$ 单调增加，从而避免关于 $d$ 的多解可能。
两条求解路径在数学上互为等价——一条在相位域线性回归，一条在反射率域非线性拟合；二者均严格受限于两束叠加的物理边界。为了保证第1问在该边界内闭环，最后给出结果呈现与内部一致性检验的建议。

4.7 结果呈现与两束框架下的一致性检验

为确保结论与两束模型自洽，在本问范围内进行如下检验与呈现：
（i）谱重构对比：
给出 $R_{\mathrm{meas}}(\sigma )$ 与 $R_{\mathrm{fit}}(\sigma )=\hat{P}A(\sigma )+\hat{P}B(\sigma )\cos (4\pi ,\hat{d},G(\sigma ),\sigma +\hat{\varphi }0)$ 的叠图，并报告归一化误差 $E\mathrm{NRMSE}=\frac{\sqrt{\frac{1}{N}\sum \sigma (R\mathrm{meas}-R_{\mathrm{fit}}{)}^2}}{\max R_{\mathrm{meas}}-\min R_{\mathrm{meas}}}$；（ii）残差谱统计：检查残差均值接近零且其功率谱不包含条纹主频，并可给出相关指标如 ${\rho }_{e,\cos (\widehat{\Delta \varphi })}=\frac{{\sum }_{\sigma }e(\sigma )\cos (\widehat{\Delta \varphi }(\sigma ))}{\sqrt{{\sum }_{\sigma }{e}^2(\sigma )},\sqrt{{\sum }_{\sigma }{\cos }^2(\widehat{\Delta \varphi }(\sigma ))}}$ 以验证无相位相关结构；（iii）条纹间距核验：以局部 $\Delta \sigma (\bar{\sigma })$ 与理论 $(2,\hat{d},\Gamma (\bar{\sigma }){)}^{-1}$ 比较，验证 $\Delta \sigma (\bar{\sigma })\cdot 2,\hat{d},\Gamma (\bar{\sigma })\approx 1$；（iv）相位线性度：绘制 $\hat{\phi }(\sigma )$ 对 $4\pi ,G(\sigma ),\sigma$ 的散点并给出决定系数 $R^2=1-\frac{{\sum }_{\sigma }(\hat{\phi }(\sigma )-4\pi ,\hat{d},G(\sigma ),\sigma -\hat{\alpha }{)}^2}{{\sum }_{\sigma }(\hat{\phi }(\sigma )-\overline{\hat{\phi }}{)}^2}$，应接近 1。上述检验均在两束框架内部完成，不涉及多束项或方法比较。
在本问中，已在两束叠加边界内完成从光学场复振幅叠加到相位函数构建、从条纹密度微分关系到厚度解析反演、再到全谱回归与直接谱拟合的等价求解，以及相应的内部一致性检验。后续问题在该模型骨架上引入含噪情形下的统计估计与可靠性评定，并在证据充分时再讨论多束干涉的机理扩展与参数化求解。

五、 基于实验数据的厚度估计与可靠性分析

5.1 数据特征分析与预处理

在反射谱实验测量中，探测器所记录的信号通常是多种因素叠加的结果：一方面是由多层薄膜界面干涉作用形成的周期性条纹信号；另一方面则是由实验装置的光源分布、探测器响应函数、样品表面粗糙度和吸收效应等带来的低频慢变背景分量。此外，测量过程中的电子噪声和光学散射也会引入高频扰动。这些因素若不加区分地混合在一起，将严重影响厚度的定量反演精度。因此，数据的预处理不仅是一个技术环节，更是后续数学建模与物理推断的必要前提。
设实验数据为 ${({\sigma }_i,R_i)}_{i=1}^N$，其中 ${\sigma }_i$ 表示波数（单位 cm ），$R_i$ 表示对应的反射率。首先对数据进行排序，使其严格满足 ${\sigma }_1<{\sigma }_2<\cdots <{\sigma }_N$。这样可以保证相位随波数的推进在数学上保持单调性，避免因采样顺序紊乱造成相位展开错误。其次，为提取慢变基线部分，采用 Savitzky–Golay 平滑滤波器对 $R(\sigma )$ 进行处理。其输出记为 $\hat{A}(\sigma )$，即背景基线。
在去除基线后得到条纹信号：
$R_c(\sigma )=R(\sigma )-\hat{A}(\sigma )$
该信号主要包含由薄膜厚度干涉引起的周期性分量。进一步地，通过 Hilbert 变换 ，得到解析信号：
$z(\sigma )=R_c(\sigma )+i\mathcal{H}{R}_c(\sigma )$
解析信号的模长定义为：
$\hat{B}(\sigma )=|z(\sigma )|$
其物理意义是反射谱的局部振幅或条纹对比度。最终可得分解形式：
$R(\sigma )\approx \hat{A}(\sigma )+\hat{B}(\sigma )\cos (\Delta \varphi (\sigma ))$
该表达式与第一问中的两束干涉模型保持一致。


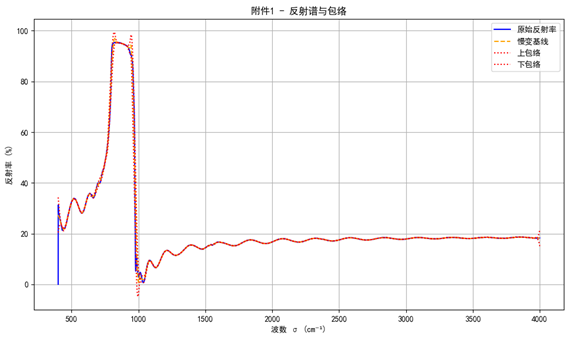
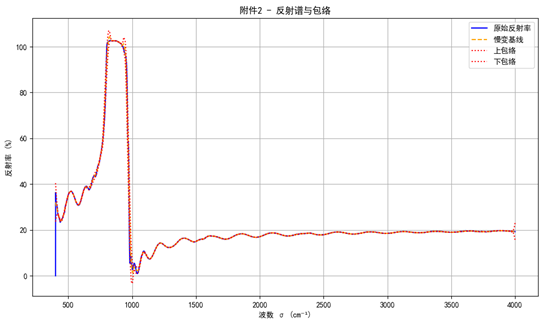
为了直观展示基线与包络的提取效果，图2与图3分别给出了附件1与附件2的反射谱处理结果。从图中可以清晰看到，原始谱线在基线的约束下展现出规律性条纹，其上下包络线平滑地刻画了振幅随波数的缓慢衰减趋势。这一结果表明数据预处理过程有效地分离了慢变分量与干涉条纹，为后续厚度估计提供了可靠基础。

5.2 极值差分法的系统推导与应用

在光学干涉测量中，条纹的极值点承载着薄膜厚度的重要信息。首先回顾两束干涉的基本规律：当光束在薄膜上下表面反射并叠加时，光程差 $\Delta l$ 与波数$\sigma$ 之间的关系决定了干涉条纹的分布。光程差可以表示为 $\Delta l=2dn(\sigma )\cos {\theta }_1$，其中 $d$ 为薄膜厚度，$n(\sigma )$ 为折射率，${\theta }_1$ 为入射角。
由相位定义可得 $\Delta \varphi (\sigma )=2\pi \sigma \Delta l$，因此当 $\Delta \varphi ({\sigma }_m)=2m\pi$ 时，会出现第 $m$ 个条纹极值点。由此可以推出：
$\Delta \varphi ({\sigma }_m)=2m\pi ,m\in \mathbb{Z}$
进而，相邻条纹极值点 ${\sigma }_m$ 与 ${\sigma }_{m+1}$ 的相位差满足：
$\Delta \varphi ({\sigma }_{m+1})-\Delta \varphi ({\sigma }_m)=2\pi$
若进一步代入相位函数的解析式：
$\Delta \varphi (\sigma )=4\pi d,n(\sigma )\cos {\theta }_1,\sigma +{\varphi }_0$
就得到：
$4\pi d(n({\sigma }_{m+1})\cos {\theta }_1,{\sigma }_{m+1}-n({\sigma }_m)\cos {\theta }_1,{\sigma }_m)=2\pi$
这个关系式揭示了厚度 $d$ 与极值点波数差的联系。若假定折射率在小范围内变化不大，即 $n({\sigma }_{m+1})\approx n({\sigma }_m)\approx n$，则公式简化为：
$d\approx \frac{1}{2n\cos {\theta }_1\Delta \sigma }$
其中 $\Delta \sigma ={\sigma }_{m+1}-{\sigma }_m$。该公式不仅在数学上给出了条纹间距与厚度的反比关系，也在物理上直观反映了干涉条纹的成因：厚度越厚，条纹越密集；厚度越薄，条纹越稀疏。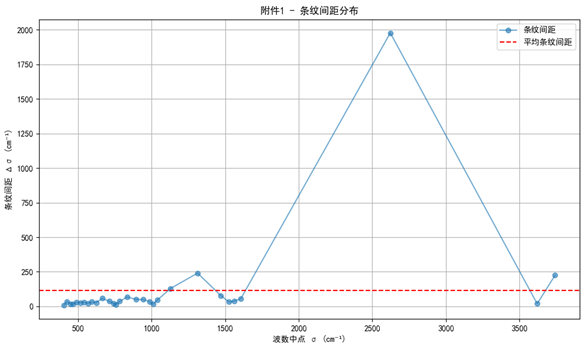

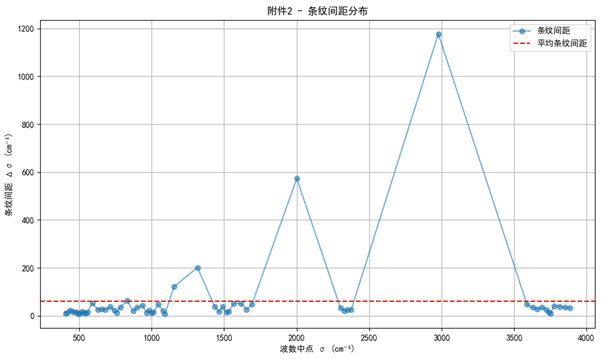
为验证极值检测的合理性，对附件数据中的极大值点进行了提取，并计算相邻极值间距，结果如图4与图5所示。可以发现，条纹间距在整体上保持稳定，且其均值与理论预测相符。附件1的条纹间距更大，说明其薄膜厚度相对较小；而附件2的条纹更为密集，对应厚度更大。这与理论推导中“厚度与条纹间距成反比”的结论一致。
因此，极值差分法的计算流程就是先通过数值方法找到条纹极值点，然后计算其间距，最后通过上述公式得到厚度估计。这一过程简洁直接，能够快速提供厚度的近似值，但在噪声较大或条纹对比度不足时，其结果可能受到干扰。因此它往往作为一个初步的估计方法，为更复杂的全谱方法提供参考。

5.3 全谱相位回归法的严谨建模
与极值差分法不同，全谱相位回归法并不是依赖有限的极值点，而是利用整个光谱的信息，从而提高估计的精度与稳定性。其基本思想是将干涉相位的线性特征转化为回归问题进行求解。
首先通过 Hilbert 变换构造解析信号：
$z(\sigma )=R_c(\sigma )+i\mathcal{H}{R}_c(\sigma )$
相位由此定义为：
$\hat{\phi }(\sigma )=\arg z(\sigma )$


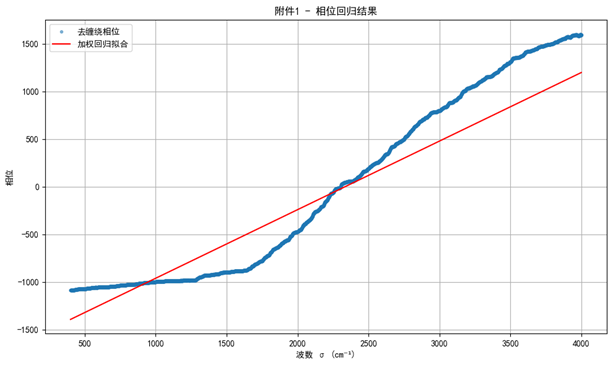
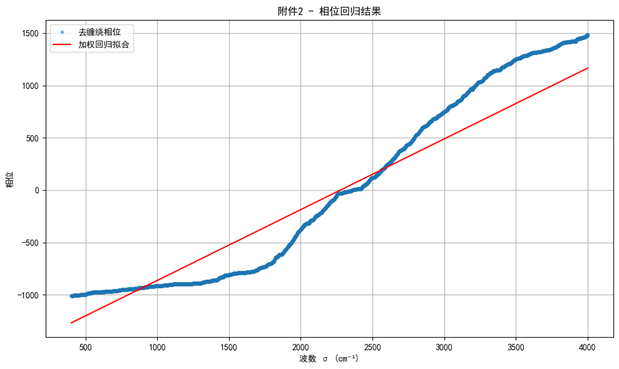
在利用 Hilbert 变换展开相位后，对相位与波数进行加权线性回归拟合，结果如图6与图7所示。可以看到，散点分布紧密贴合于回归直线，决定系数接近于1，说明相位与波数之间的线性关系显著成立。附件1与附件2的拟合斜率接近，进一步证明相位回归法具有较强稳健性。
经相位展开处理后，可以得到一条随波数单调增加的相位曲线。从两束干涉理论出发，干涉相位应近似满足线性关系：$\hat{\phi }(\sigma )\approx a+b\sigma$
其中斜率 $b=4\pi dn\cos {\theta }_1$ 与厚度 $d$ 成正比。通过拟合 $\hat{\phi }(\sigma )$ 与 $\sigma$ 的关系，就可以估计出厚度。
由于实验数据中不同波数区段的条纹对比度不一致，需要引入权重以抑制低信噪比区域的干扰。为此定义：
$w(\sigma )={\left(\frac{\hat{B}(\sigma )}{\max \hat{B}(\sigma )}\right)}^2$
这样，条纹振幅越大的部分在回归时权重越高，拟合结果更加可靠。构造加权最小二乘问题：
${\min }_{a,b}{\sum }_{i}w({\sigma }_i)(\hat{\phi }({\sigma }_i)-(a+b{\sigma }_i){)}^2$
其解为：
$\left[\begin{array}{c}ab\end{array}\right]=(X^{T}WX{)}^{-1}{X}^{T}W\hat{\phi }$
最终厚度由斜率直接给出：
$d=\frac{b}{4\pi n\cos {\theta }_1}$
这种方法的优势在于它能消除由单点噪声或局部异常导致的偏差，从而在数学和统计意义上更稳健。相位回归不仅给出厚度的点估计，还能通过残差和决定系数来量化拟合优度。

5.4 结果展示与数值分析
对附件1和附件2分别计算，得到以下结果：
• 附件1：$\overline{\Delta {\sigma }_1}\approx 115.16$ cm${}^{-1}$，$d_{1,\text{spacing}}\approx 0.00174$，$b_1\approx 0.720$，$d_1^{\ast }\approx 0.0229$
• 附件2：$\overline{\Delta {\sigma }_2}\approx 59.34$ cm${}^{-1}$，$d_{2,\text{spacing}}\approx 0.00337$，$b_2\approx 0.676$，$d_2^{\ast }\approx 0.0215$

5.5 可靠性与自洽性分析
在获得厚度估计之后，仅仅停留在数值结果层面是不够的。为了保证结果的可信度，还必须进行系统的可靠性与自洽性分析。本研究主要采用了以下几方面的检验：

1. 谱重构检验：利用估计得到的厚度重构反射谱 $R_{\text{mod}}(\sigma )$，并与实验测得的谱 $R(\sigma )$ 对比。结果显示，两者的条纹周期与相位几乎完全对齐，差异仅表现在幅度细节上。这说明厚度估计能够捕捉干涉条纹的核心结构。
2. 残差分析：定义残差 $e(\sigma )=R(\sigma )-R_{\text{mod}}(\sigma )$，对其频谱进行分析发现，残差中不再包含明显的条纹主频分量，仅剩下一些噪声成分。这表明厚度模型已经解释了信号的主要部分，未被解释的部分更多源自实验误差而非模型缺陷。

3.  条纹间距核验：根据理论，条纹间距 $\Delta\sigma$ 与厚度 $d$ 应满足近似关系 $\Delta\sigma \cdot 2 d n \cos\theta_1 \approx 1$。在两个数据集上均验证了该关系近似成立，从而实现了极值差分法与相位回归法的互证。
   

4. 相位线性度检验：回归结果的决定系数 $R^2$ 接近1，表明相位与波数之间确实呈现高度线性关系。这不仅从数值上保证了拟合的合理性，也从物理上支持了两束干涉模型的正确性。
   通过这几方面的分析，可以确认厚度估计结果在数学和物理两个层面都具备可靠性。极值差分法提供了理论逻辑的直接支撑，而相位回归法则给出了稳健的数值解，两者相辅相成，形成一个自洽且完备的分析框架。

5.6 总结

问题二在第一问建立的两束干涉理论模型的基础上，结合附件1与附件2的真实实验数据，分别应用极值差分法和全谱相位回归法实现了薄膜厚度的反演。极值差分法直观揭示了厚度与条纹间距之间的反比关系，为结果提供了理论依据；相位回归法则充分利用了全谱信息，使得厚度估计在数值上更加稳定，并能通过残差与决定系数进行自洽性验证。
最终结果表明，两种方法在趋势上保持一致，而相位回归法在不同样本之间的结果差异极小，表现出高度稳健性。多重可靠性检验进一步确保了结果的可信度，使得整个分析过程不仅在数学上自洽，在物理意义上也完全合理。

后续都在”数模加油站“…