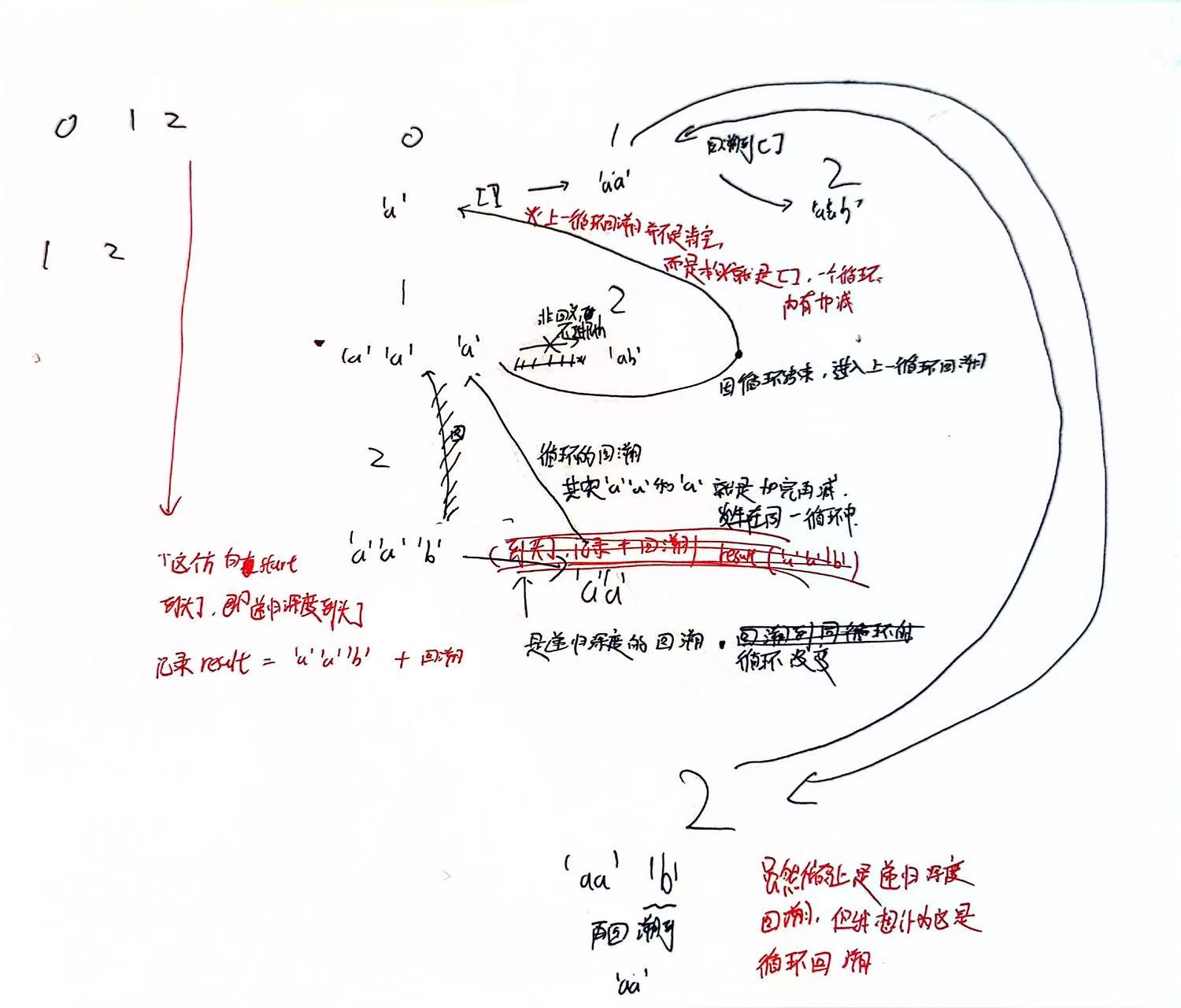
分割回文串手绘图
每一次循环内会新增一个再减一个 所以回溯会一个循环内时会恢复其本身的样子,减回原来的样子。
回文串分割的回溯条件深度解析
回溯算法的核心在于**“选择”和“撤销选择”,而“回溯条件”**(即何时返回)则是控制递归深度的关键。在你的代码中,回溯条件主要有以下两个:
1. 递归的结束条件(找到一个解)
这是第一个也是最重要的回溯条件,它标志着我们成功地找到了一条通向完整解的路径。
代码中的体现:
if start == len(s):解释:
start变量代表当前正在处理的子字符串的起始索引。当
start的值等于字符串s的长度len(s)时,意味着我们已经成功地将整个字符串s从头到尾全部切分完毕,并且每一步切分出的子串都是回文串。此时,
path列表中存储的就是一个完整的、有效的分割方案。我们的任务是将这个完整的方案(
path的一个副本)添加到最终的结果集result中,然后返回。这个返回操作就是一次“回溯”,它让程序回到上一层递归,继续探索其他可能的分割路径。
可以想象成你在迷宫里找到了一个出口。找到后,你当然要把这个出口记录下来,然后回到上一个岔路口,尝试走另一条路去寻找其他的出口。
2. for 循环的自然结束(当前路径没有更多选择)
这是另一个隐含的回溯条件,它发生在**for 循环**的层面。
代码中的体现:
for i in range(start, len(s)):解释:
for循环负责在当前递归层级中,遍历所有可能的**“下一个分割点”**。循环变量
i决定了我们从start位置截取到哪里。当for循环从start遍历到len(s) - 1,并且所有尝试的子串s[start:i+1]都不是回文串,或者即使是回文串,但在其后续递归调用中也无法找到完整解时,这个for循环就会自然结束。当循环结束后,
backtrack函数执行完毕,它会自动返回到上一层递归调用。
这就像你在迷宫的一个岔路口,尝试了所有可能的路,但都没有找到出口。当你试完所有路后,你就不得不退回到更上一个岔路口,去尝试那里的其他路径。
总结
回溯算法在解决这类问题时,正是通过这两种“回溯条件”来控制递归的。
start == len(s):这是一个成功的回溯,意味着我们找到一个解,然后返回去寻找其他解。for循环结束:这是一个失败的回溯(或者说是“此路不通”),意味着在当前层级没有更多可行的选择,必须返回上一层去重新选择。
这两种机制共同构成了回溯算法的完整流程,确保我们能系统地、不遗漏地探索出所有可能的解决方案。
