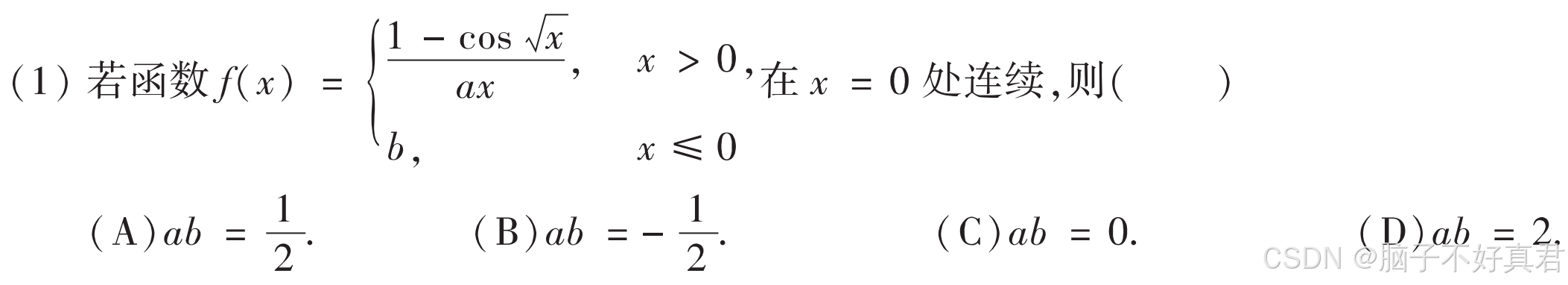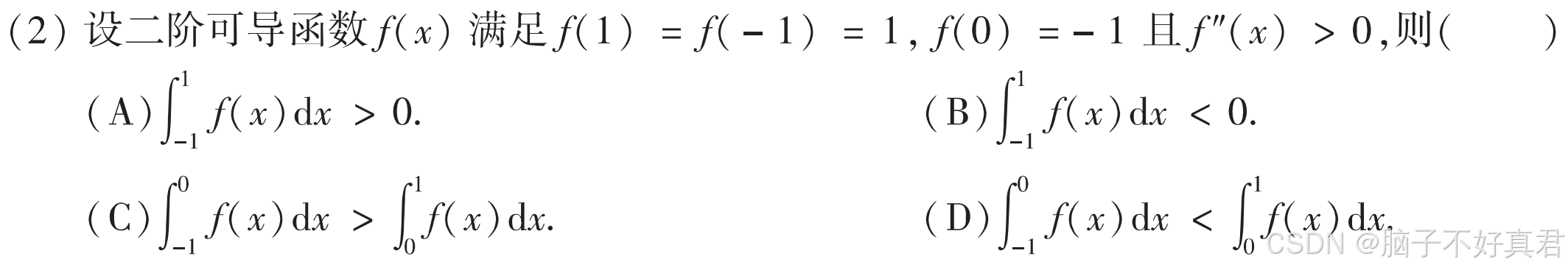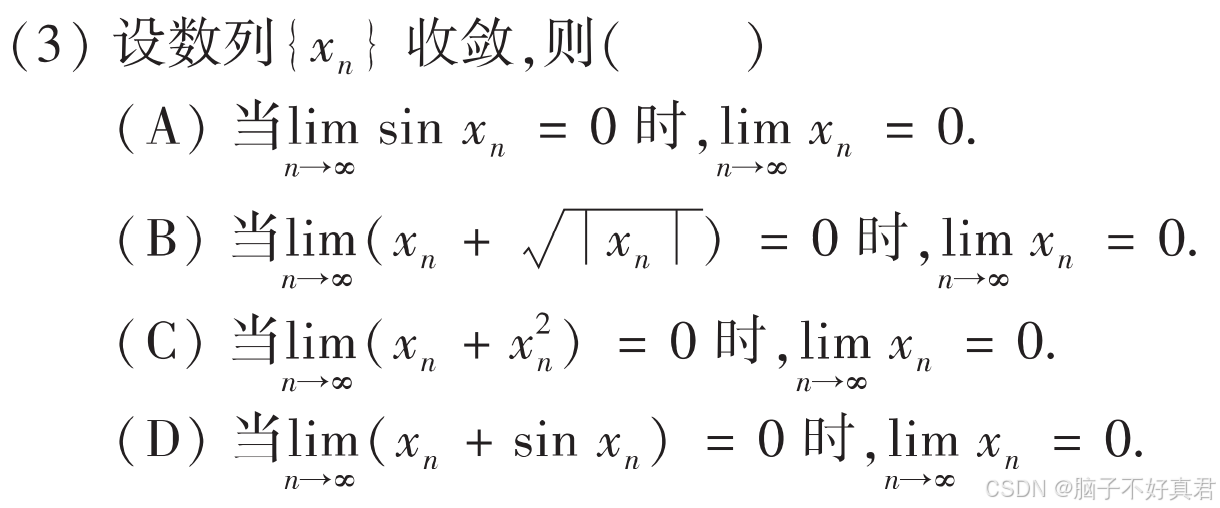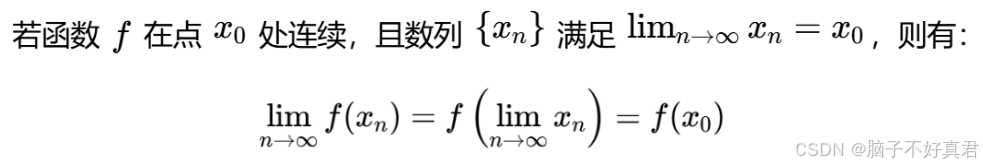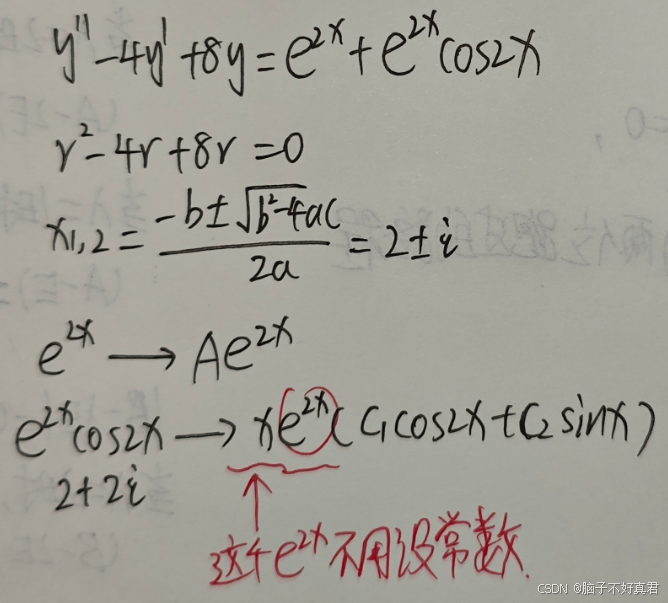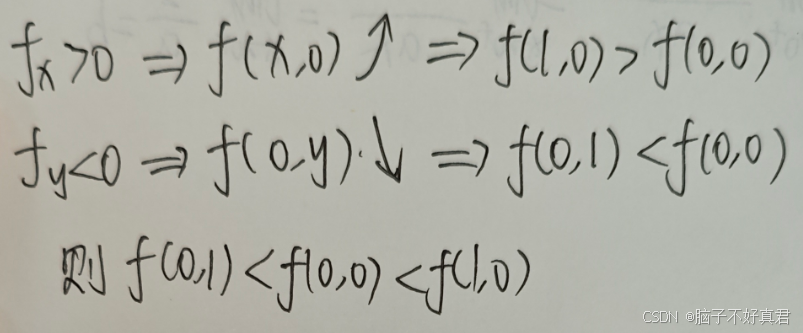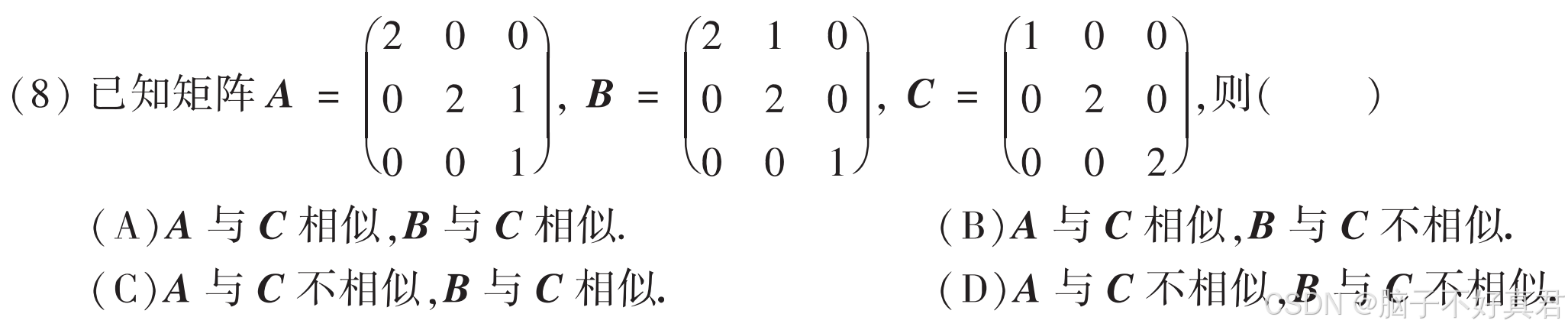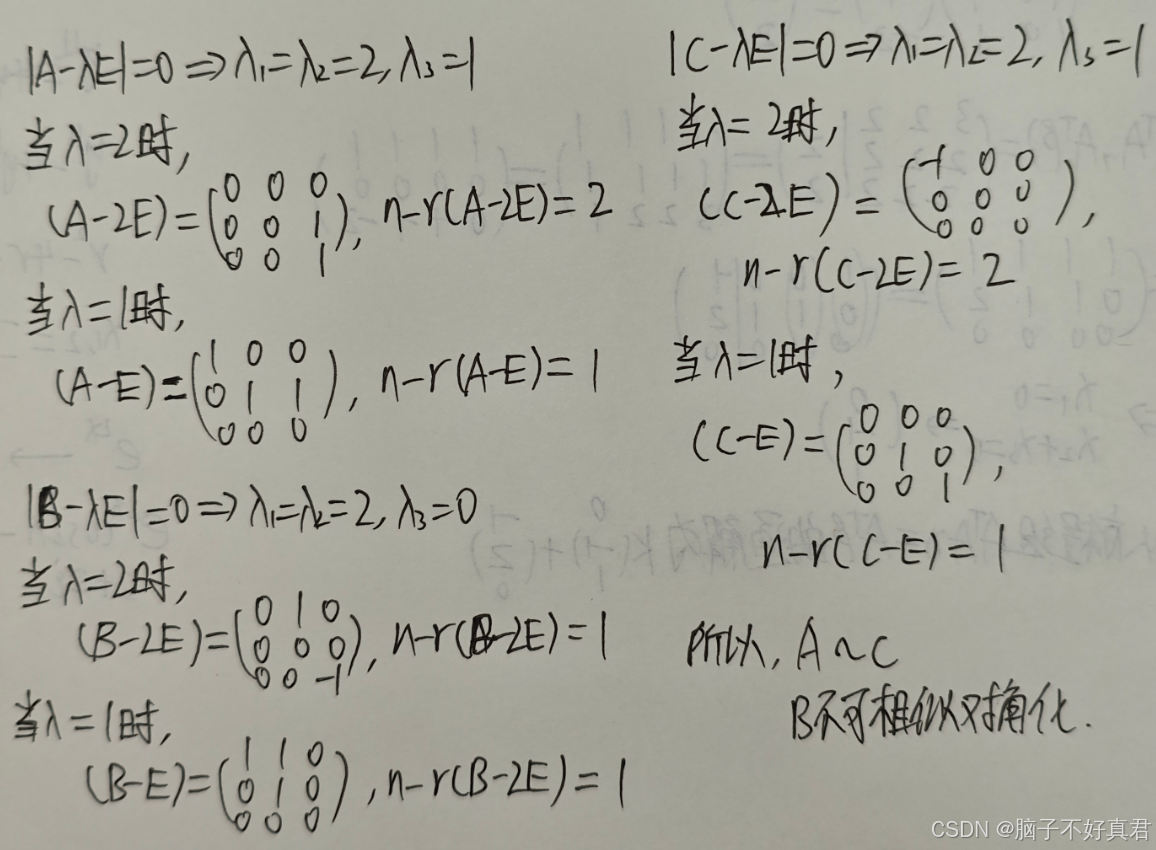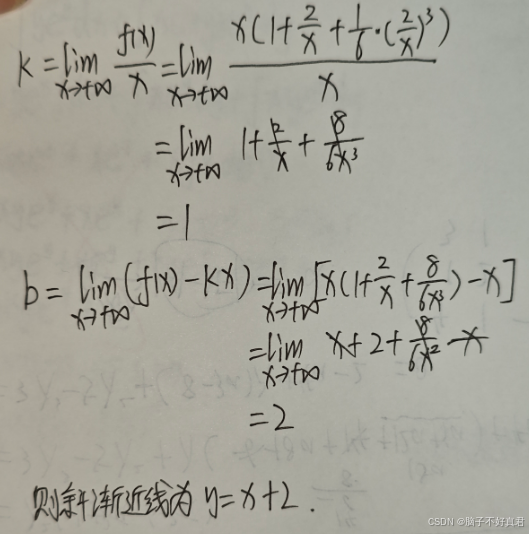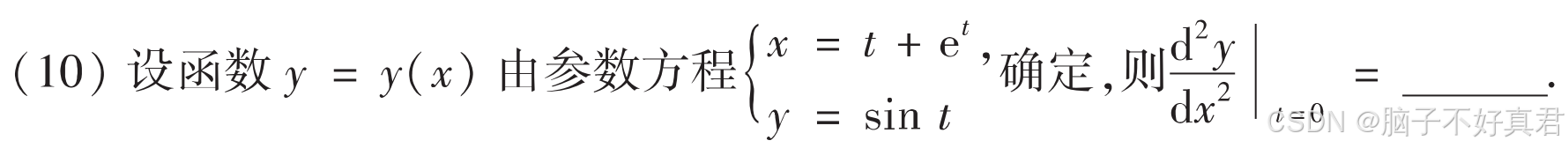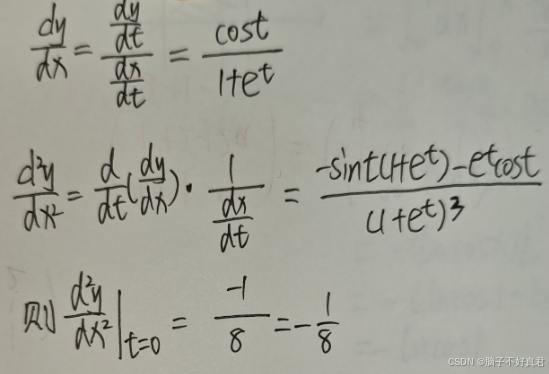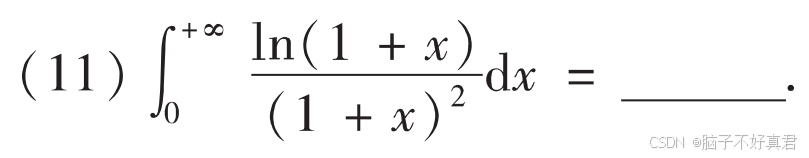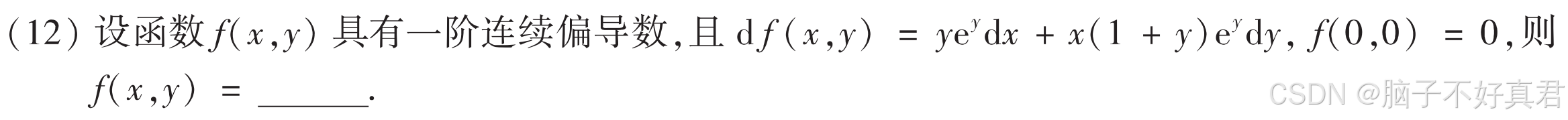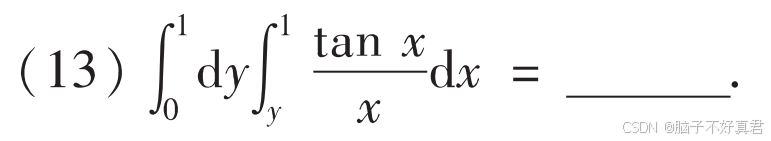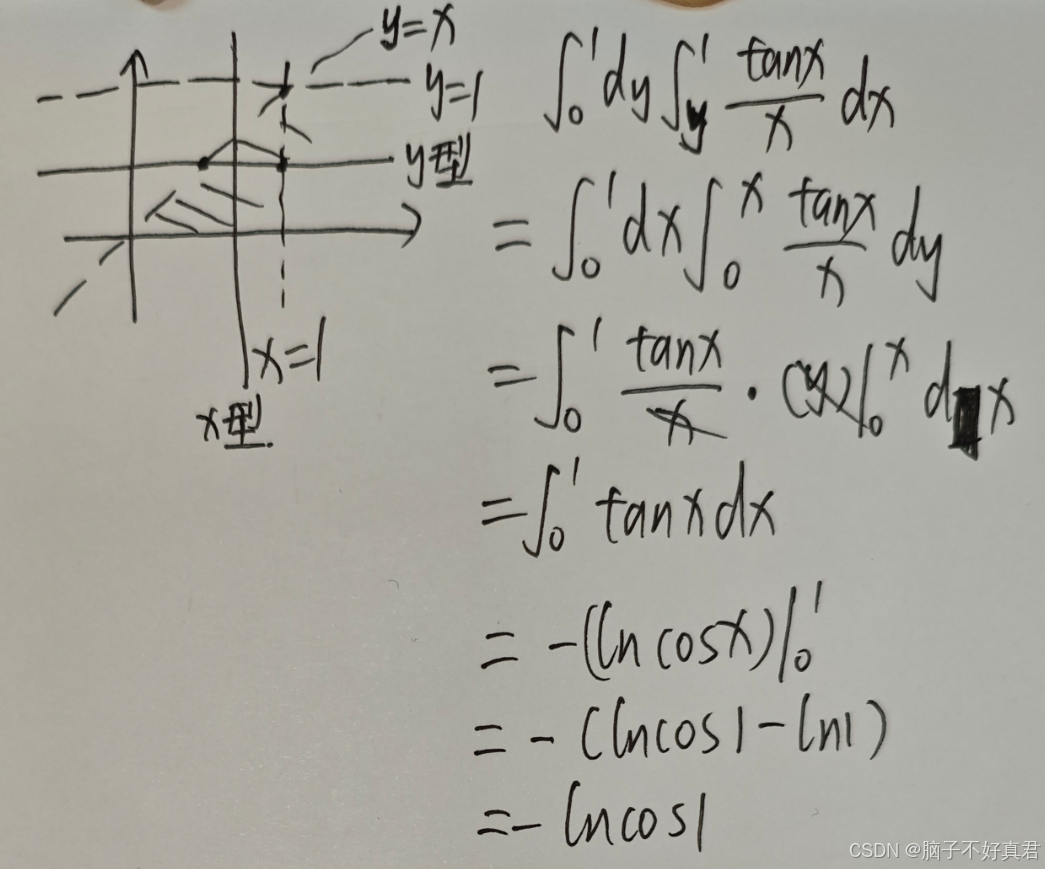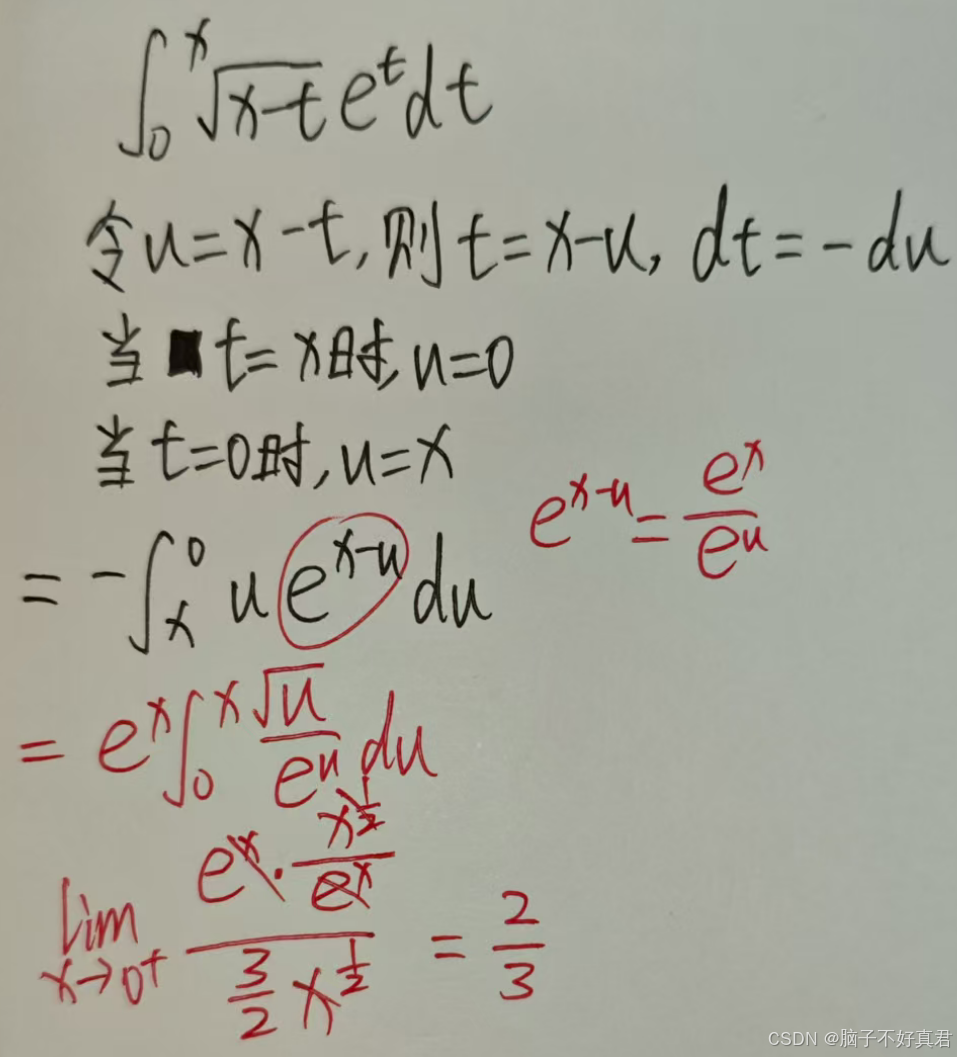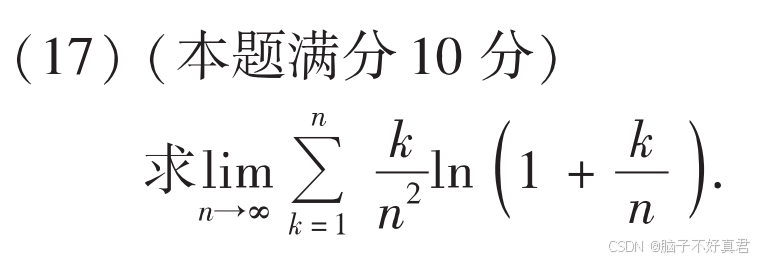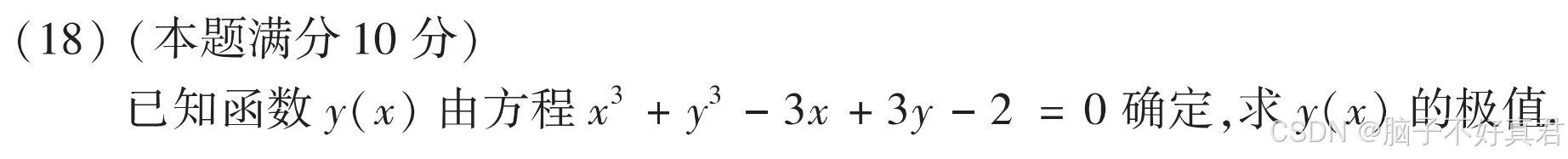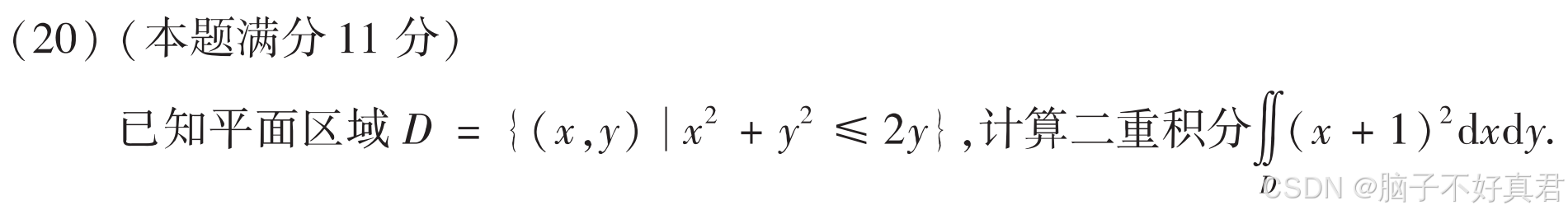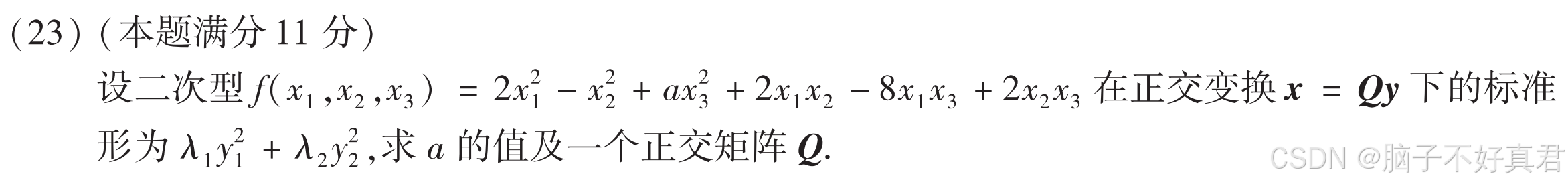2017考研数学（二）真题

一、选择题

(1)

考点：

cosx的麦克劳林展开、

连续的定义

(2)

考点：

特殊值法

凹函数图像性质（在选择题中常考凹凸曲线的性质）

方法一：

方法二：

(3)

考点：

👇、

排除法、

如果函数连续，极限运算与函数运算可以交换顺序​​

方法一：

方法二：

(4)

考点：

二阶非齐次线性微分方程的 特解设法、

求根公式

(5)

考点：

把二元函数中的一个变量视为常数，则此时二元函数可视为一元函数

(6)

考点：

图像面积的物理意义、

不用害怕，精心细心做

(7)

考点：

矩阵的相似对角矩阵就是矩阵特征值、

Aλ=λα           

(8)

考点：

对于矩阵A的每一个特征值 λ，它的几何重数都必须严格等于它的代数重数 矩阵才可相似对角化、

λ1: 代数重数是2，几何重数是1；λ2: 代数重数是1，几何重数是1”​​ 这种情况在数学上​​是不可能发生的

二、填空题

(9)

(10)

(11)

(12)

考点：识别出全微分公式

(13)

(14)

三、解答题

(15)

考点：拆e^(x-u)

(16)

(17)

(18)

★有遗漏知识点(19)

考点：👇

(Ⅰ)

(Ⅱ)

(20)

考点：普通对称性、

           被积函数为1的二重积分结果为积分区域面积

(21)

考点：微分方程的应用、

           齐次微分方程求解、

           切线斜率与法线斜率互为负倒数、

           k=(x2-x1)/(y2-y1)

方法一：

方法二：

(22)

考点：

一个n阶矩阵有n个不同的特征值，那么此矩阵就可相似对角化

不同特征值对应的特征向量线性无关、

回归到Ax=0的形式        

(Ⅰ)

(Ⅱ)

(23)