当前位置：首页 > java >正文

LeetCode刷题记录----51.N皇后（Hard）

java 2025/9/2 7:54:38

2025/8/30

题目（Hard）：

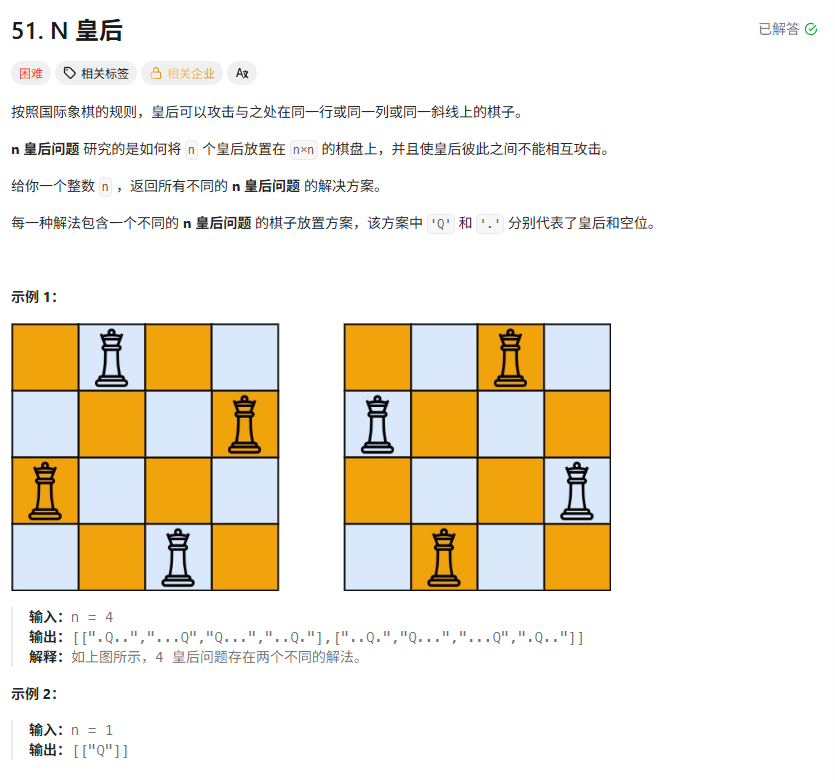
我的思路：

我们知道，对于每一个皇后来说，她的攻击路线有：一行，一列，主斜线，副斜线四种。而当我们每次放下一个皇后之后，他的这些攻击路线就会生效到该棋盘的每一个可攻击的格子上。

因此，我们可以用一个数组来标记当前格子是否能够被皇后攻击到。

然后因为我们知道如果当前行有了皇后之后，就不可以再放另一个皇后，因此我们可以按行来放置每一个皇后。这就可以用到递归回溯的思想去枚举每一行的可放置皇后的位置，当前递归层的这一行上的格子是否可以放置皇后是由之前的行决定的，而我们在这里可放置皇后的位置放置了新的皇后之后，又会影响到下一行。

当我们回溯到当前行后，我们需要撤销之前放置后产生的影响，但是如果我们只是单纯地以bool值来标记每个各自是否可以放置，就会把还没回溯到的行上皇后产生的影响给覆盖掉，因此我们对每个格子的定义改变为【当前格子会被几个皇后攻击到】，所以回溯到当前行的时候，把可攻击皇后-1即可。相对应的，在行上放置一个皇后的时候，对他所能影响到的格子的可攻击皇后数+1即可

因此我们的大致思路是：

①递归终止条件：当前所在的行索引值 == n，此时把这一组放置的方法加入到结果中

②递归的每一层只处理当前行，遍历当前行的每一列，如果找到的位置上的可攻击皇后数为0，则在这里放置一个皇后，并更新她对其他格子造成的攻击影响数。

③递归调用函数，处理下一行

④回溯到当前行后，先把皇后移除，然后撤销她对其他格子造成的攻击影响

⑤所有递归结束之后，返回答案集

具体代码如下：

class Solution {
private:vector<vector<string>> res;vector<string> output;vector<vector<int>> canSet;    //标记可以每个位置会被几个皇后攻击的二维数组int n;  //长度void backTrack(int row){if(row == n){res.emplace_back(output);return;}string curRowSet(n, '.');for(int i = 0; i < n; i++){if(canSet[row][i] == 0){curRowSet[i] = 'Q' ;output.emplace_back(curRowSet);updateCanSet(row, i, 1); //更新canSet表//递归处理下一行backTrack(row + 1);//回溯到当前位置后撤销之前的更改curRowSet[i] = '.';output.pop_back();updateCanSet(row, i, -1);}}}//给每个位置标记当前位置会遭到几个皇后的攻击，value传入1表示会多被一个皇后攻击到，value传入-1表示撤销当前皇后在该处的攻击void updateCanSet(int row, int column, int value){for(int i = 0; i < n; i++){canSet[row][i] += value;     //行canSet[i][column] += value;  //列int offset = i - column;    //斜线if(row + offset > 0 && row + offset < n)canSet[row + offset][i] += value;if(row - offset > 0 && row - offset < n)canSet[row - offset][i] += value;//canSet[row][column] -= value * 3;   //放置的位置被多标记了3次}}public:vector<vector<string>> solveNQueens(int n) {this->n = n;canSet.assign(n, vector<int>(n, 0));backTrack(0);return res;}
};

时间复杂度：O(N! × N²)【有大约 O(N!) 种有效配置，每种配置需要 O(N) 次 updateCanSet 调用，每次 updateCanSet 需要 O(N) 时间】

空间复杂度：O(N²)【除去存储答案的空间外，额外需要的空间是栈递归的深度，需要递归皇后数量N的层，以及canSet攻击影响数组需要O（N²）的空间】

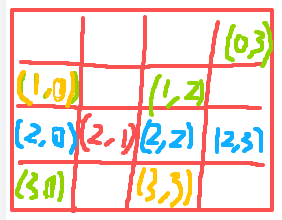
这里对于更新攻击影响的时候，关于对角线的位置更新。

这里比如我们在（2，1）放置了皇后。我们可以很轻松地横着更新他的攻击影响（蓝色位置）。而对于对角线，我们先看黄色部分的，他的列数和列更新部分一样的，不一样的只是行的值，而这个值我们可以看到是和他的列以及皇后的列数是有关系的。比如黄色（1，0）部分，他的行数1 = （2 + （0-1）),其中2是皇后所在的行数，（0-1）中0是黄色（1，0）所在的列，1则是皇后所在的行数。因此通过这样的计算我们可以得到当前列皇后影响到的斜线上的格子。其他斜线上的格子同理。