GaussianLSS
背景
BEV感知能够聚合多个传感器输入得到统一的空间表征,在3D感知、下游应用以及跨模态融合中发挥重要作用。现有的BEV感知分为2D反投影(LSS)以及3D投影(BEVFormer),其中3D投影依赖于3D体素的投影,这导致BEV网格分辨率不能太大,否则计算代价高。本文提出了基于2D反向投影方法,在准确度与计算效率间取得平衡并满足实时性要求。
相关工作
投影方法
对于3D投影来说,相比于2D反投影它是计算密集型的,对网格分辨率有较高要求,限制了在现实场景下的可扩展性。
对于2D反投影来说,LSS提出将2D特征抬升到3D空间中,但他依赖于准确的深度估计,深度估计错会传播到BEV表征中,因此后续的BEVStereo、BEVDepth都引入了深度损失作为辅助损失。虽然它们使用了概率深度估计来soft的抬升特征,但是还是缺乏显式的深度不确定性的表示,在复杂场景下很难处理深度模糊性的问题。GaussianLSS通过计算概率深度分布的方差来建模深度不确定性,从而降低了对于准确深度的依赖转为捕获围绕均值深度的空间范围。
不确定性建模
不确定性建模就是在建模或预测时不是给出一个准确的值,而是给出预测结果+结果的信心程度。评估不确定性的方法包含以下几种:
- 预测分布的方差。计算概率分布的方差,从而在输出中提供直接反映信心程度的信息。
- 基于MLP的不确定评估。它是通过多层的MLP网络得到一个不确定性分数,又或者是输出一个分布的参数u与σ,其中σ作为方差衡量不确定性。
- 贝叶斯网络。使用分布的先验建模不确定性。
在这篇论文中,则是通过分布的方差来建模不确定性从而提升BEV表征,尤其是在深度模糊的情况下。
主要工作
深度不确定性建模
LSS的主要问题:1、离散深度导致稀疏BEV,空间覆盖率低。2、不稳定的深度分布,softmax得到的深度概率即使两个bin靠近也可能大不相同,从而导致BEV特征不一致,这是由于softmax会是大的更大,小的更小,深度值轻微的不同可能导致不成比例的深度关注度。
本文是在预测的深度分布的基础上计算它的均值与方差,使用错误容忍因子得到[u-kσ,u+kσ]的范围,这个范围考虑了深度不确定性,实现更灵活可靠的深度投影。
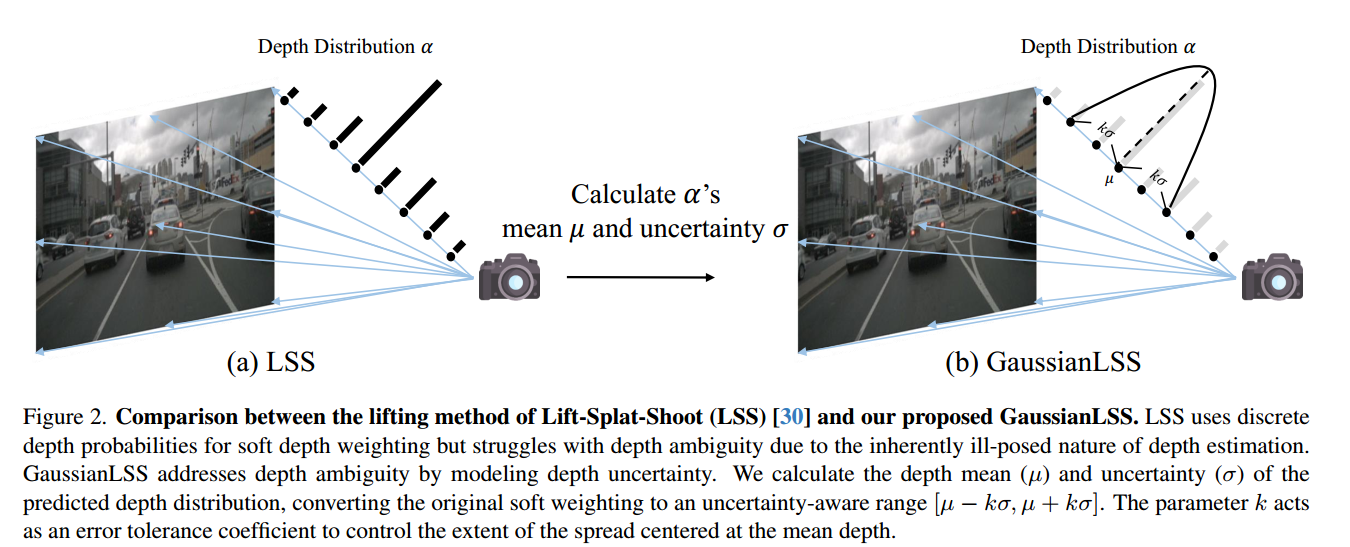
3D不确定性变换
对得到的深度范围点,通过内外参转换到自车坐标系下,计算出每个像素对应的均值与协方差,公式如下:
μ3d=∑i=0B−1Pi(p) pi3d \mu _{3d} = \sum _{i=0}^{B-1} P_i(p) \, p^{3d}_i μ3d=i=0∑B−1Pi(p)pi3d
Σ=∑i=0B−1Pi(p) (pi3d−μ3d)(pi3d−μ3d)T \Sigma = \sum_{i=0}^{B-1} P_i(p) \, (p^{3d}_i - \mu_{3d})(p^{3d}_i - \mu_{3d})^TΣ=i=0∑B−1Pi(p)(pi3d−μ3d)(pi3d−μ3d)T
使用马氏距离定义置信范围,利用了上面使用过的错误容忍系数,公式如下:
(x−μ3d)TΣ−1(x−μ3d)≤k2(x - \mu_{3d})^T \Sigma^{-1} (x - \mu_{3d}) \leq k^2(x−μ3d)TΣ−1(x−μ3d)≤k2
BEV Features Splatting
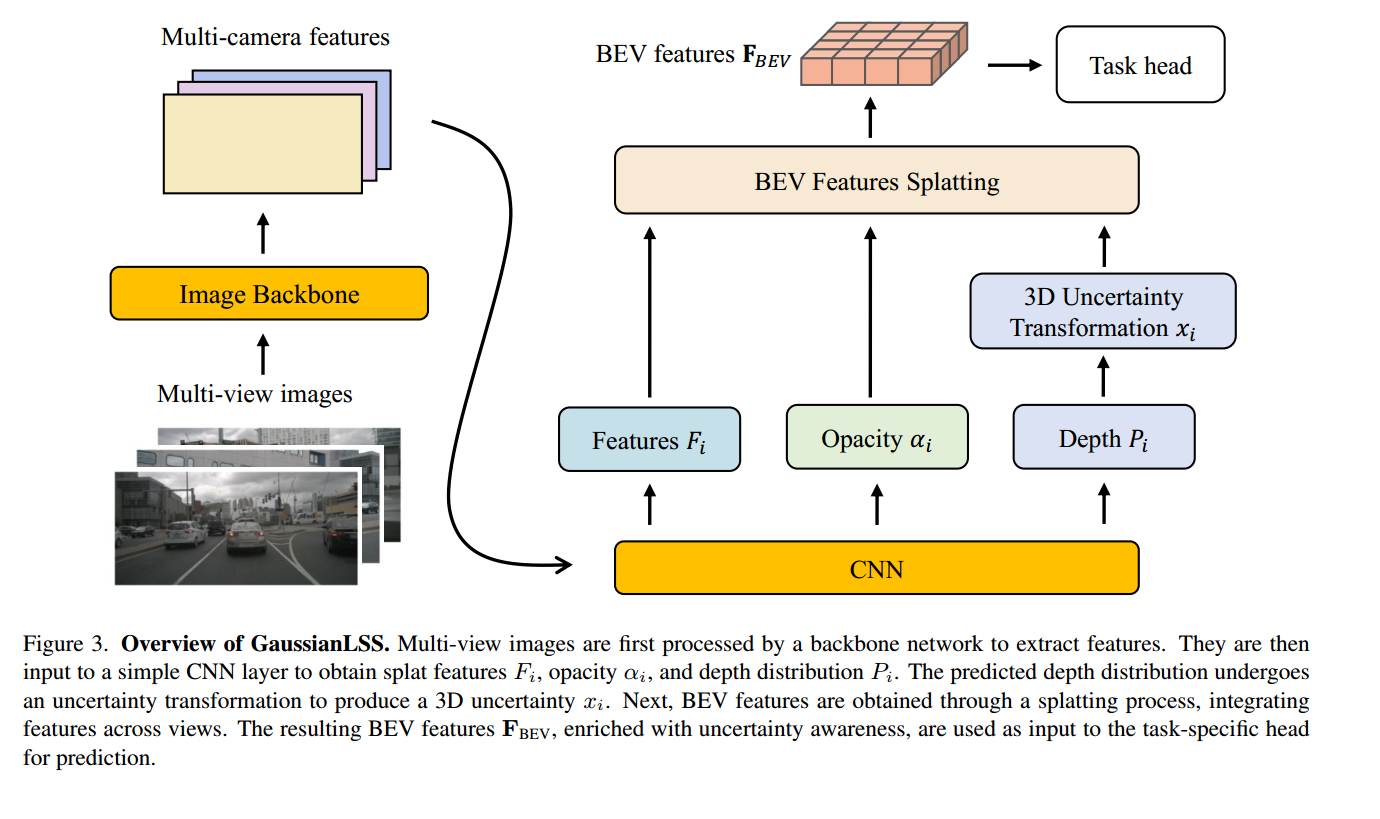
对于提取的特征分别输出context,opacity与depth,其中depth通过3D不确定性变换得到两个参数作为后续的输入,利用Gaussian Splatting投射到BEV视角。
FBEV(x)=∑i∈GBEVFiαiexp(−12(x−μi)⊤Σi−1(x−μi))F_{BEV}(x) = \sum_{i \in G_{BEV}} F_i \alpha_i \exp\left(-\frac{1}{2} (x - \mu_i)^\top \Sigma_i^{-1} (x - \mu_i)\right)FBEV(x)=i∈GBEV∑Fiαiexp(−21(x−μi)⊤Σi−1(x−μi))
此外考虑到相邻像素深度上的差异性,使用了多尺度BEV进行处理,最后进行上采样。
实验结果
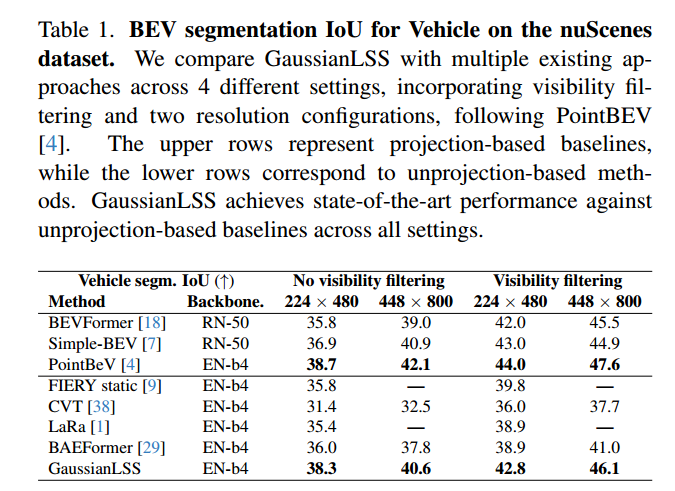
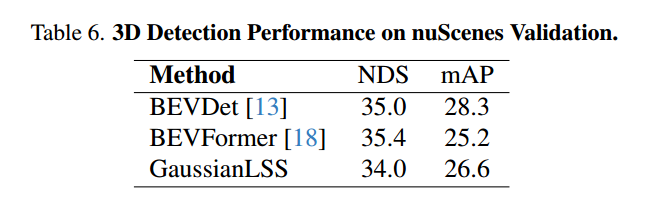
总结
GaussianLSS通过创新性地结合深度不确定性建模与高效的多尺度BEV特征渲染,成功解决了深度模糊性的固有挑战。这种方法不仅在基于反投影的方法中实现了最先进的性能,还在降低计算资源需求方面表现出色,使其特别适合自动驾驶的实时应用场景。
GaussianLSS的成功证明了显式不确定性建模在提升空间感知任务性能中的价值,为未来BEV感知系统的发展提供了新的研究方向。
