代码随想录算法训练营四十六天|图论part04
岛屿问题(八)岛屿的周长
题目描述
给定一个由 1(陆地)和 0(水)组成的矩阵,岛屿是被水包围,并且通过水平方向或垂直方向上相邻的陆地连接而成的。
你可以假设矩阵外均被水包围。在矩阵中恰好拥有一个岛屿,假设组成岛屿的陆地边长都为 1,请计算岛屿的周长。岛屿内部没有水域。
输入描述
第一行包含两个整数 N, M,表示矩阵的行数和列数。之后 N 行,每行包含 M 个数字,数字为 1 或者 0,表示岛屿的单元格。
输出描述
输出一个整数,表示岛屿的周长。
输入示例
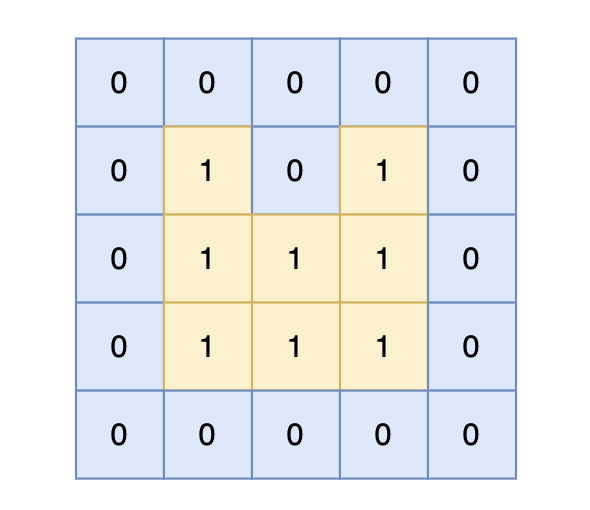
5 5
0 0 0 0 0
0 1 0 1 0
0 1 1 1 0
0 1 1 1 0
0 0 0 0 0
输出示例
14
提示信息
岛屿的周长为 14。
数据范围:
1 <= M, N <= 50。
思路:
首先为了防止有的岛屿外没有水包围,我们给原有的矩阵外包一圈水。
之后遍历矩阵(不需要遍历外面那一圈水),如果当前坐标是陆地,那么遍历它上下左右看是否有水,如果有的话,那一条边就是周长的一部分,就需要算在周长里。
代码如下:
import java.util.*;public class Main{private static int ans=0;public static void main(String[] args){Scanner in=new Scanner(System.in);int n=in.nextInt();int m=in.nextInt();int[][] graph=new int[n+2][m+2];for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){graph[i][j]=in.nextInt();}}boolean[][] visited=new boolean[n+2][m+2];for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){if(graph[i][j]==1&&visited[i][j]==false){visited[i][j]=true;dfs(graph,visited,i,j);}}}System.out.println(ans);}private static int[][] dir={{0,1},{1,0},{-1,0},{0,-1}};public static void dfs(int[][] graph,boolean[][] visited,int x,int y){for(int i=0;i<4;i++){int nextx=x+dir[i][0];int nexty=y+dir[i][1];if(nextx<0||nexty<0||nextx>=graph.length||nexty>=graph[0].length)continue;if(graph[nextx][nexty]==0)ans++;if(graph[nextx][nexty]==1&&visited[nextx][nexty]==false){visited[nextx][nexty]=true;dfs(graph,visited,nextx,nexty);}}}
}字符串接龙
题目描述
字典 strList 中从字符串 beginStr 和 endStr 的转换序列是一个按下述规格形成的序列:
序列中第一个字符串是 beginStr。
序列中最后一个字符串是 endStr。
每次转换只能改变一个位置的字符(例如 ftr 可以转化 fty ,但 ftr 不能转化 frx)。
转换过程中的中间字符串必须是字典 strList 中的字符串。
beginStr 和 endStr 不在 字典 strList 中
字符串中只有小写的26个字母
给你两个字符串 beginStr 和 endStr 和一个字典 strList,找到从 beginStr 到 endStr 的最短转换序列中的字符串数目。如果不存在这样的转换序列,返回 0。
输入描述
第一行包含一个整数 N,表示字典 strList 中的字符串数量。 第二行包含两个字符串,用空格隔开,分别代表 beginStr 和 endStr。 后续 N 行,每行一个字符串,代表 strList 中的字符串。
输出描述
输出一个整数,代表从 beginStr 转换到 endStr 需要的最短转换序列中的字符串数量。如果不存在这样的转换序列,则输出 0。
输入示例:
6
abc def
efc
dbc
ebc
dec
dfc
yhn
输出示例
4
提示信息
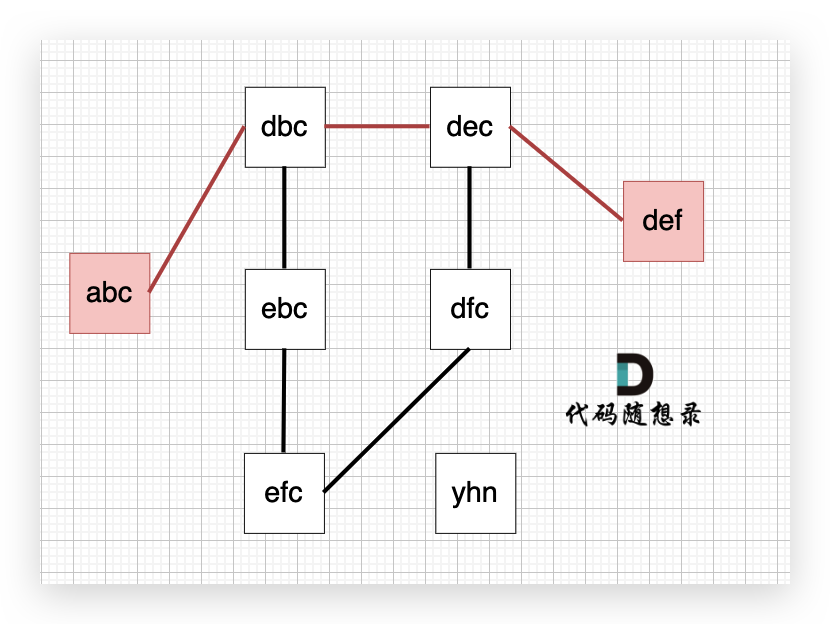
从 startStr 到 endStr,在 strList 中最短的路径为 abc -> dbc -> dec -> def,所以输出结果为 4,如图:
数据范围:
2 <= N <= 500
思路:
首先我们要解决两个问题:
1.图中的边是怎么来的?我们用26个英文字母替换当前字符串的每一个字符,看替换后是否在strList中出现过,如果出现过,那么这里就有一条边。
2.起点和终点的最短路径长度:
直接使用广搜法,只要搜到了终点(也就是endString),那么就一定是最短路径。这里如果用深搜法会比较麻烦,因为需要再到达终点的不同路径中选一条最短路径。
需要注意的是我们需要标记节点是否走过,这里使用set集合来检查会更快一点。
代码如下:
import java.util.*;public class Main{public static void main(String[] args){Scanner in=new Scanner(System.in);int n=in.nextInt();String begin=in.next();String end=in.next();List<String> list=new ArrayList<>();list.add(begin);list.add(end);for(int i=0;i<n;i++){list.add(in.next());}int ans=bfs(begin,end,list);System.out.println(ans);}public static int bfs(String begin,String end,List<String> list){int len=1;Set<String> set=new HashSet<>();//相当于visitedQueue<String> q=new LinkedList<>();q.offer(begin);q.offer(null);while(!q.isEmpty()){String tmp=q.poll();if(tmp==null){if(!q.isEmpty()){len++;q.offer(null);}continue;}set.add(tmp);char[] array=tmp.toCharArray();for(int i=0;i<array.length;i++){char old=array[i];for(char ch='a';ch<='z';ch++){array[i]=ch;String newString=new String(array);if(!set.contains(newString)&&list.contains(newString)){set.add(newString);q.offer(newString);if(newString.equals(end))return len+1;}}array[i]=old;}}return 0;}
}有向图的完全联通
题目描述
给定一个有向图,包含 N 个节点,节点编号分别为 1,2,...,N。现从 1 号节点开始,如果可以从 1 号节点的边可以到达任何节点,则输出 1,否则输出 -1。
输入描述
第一行包含两个正整数,表示节点数量 N 和边的数量 K。 后续 K 行,每行两个正整数 s 和 t,表示从 s 节点有一条边单向连接到 t 节点。
输出描述
如果可以从 1 号节点的边可以到达任何节点,则输出 1,否则输出 -1。
输入示例
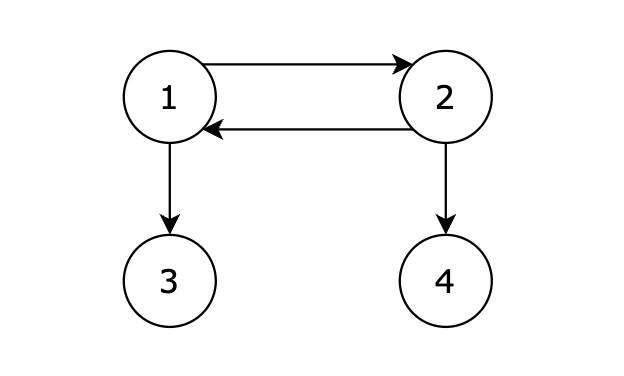
4 4
1 2
2 1
1 3
2 4
输出示例
1
提示信息
从 1 号节点可以到达任意节点,输出 1。
数据范围:
1 <= N <= 100;
1 <= K <= 2000。
思路:
深搜法,如果节点1可以到达节点2,继续看节点2能否到达其他节点,如果节点2能到达其他节点,说明节点1也可以到达这些节点,将这些节点都标记为true。最后遍历所有节点是否都标记为true,如果是的话输出1,否则输出-1。
代码如下:
import java.util.*;public class Main{public static void main(String[] args){Scanner in=new Scanner(System.in);int n=in.nextInt();int k=in.nextInt();int[][] graph=new int[n+1][n+1];for(int i=0;i<k;i++){int x=in.nextInt();int y=in.nextInt();graph[x][y]=1;}boolean[] visited=new boolean[n+1];visited[1]=true;dfs(graph,visited,1,n);for(int i=1;i<=n;i++){if(visited[i]==false){System.out.println(-1);return;}}System.out.println(1);}public static void dfs(int[][] graph,boolean[] visited,int x,int n){for(int j=1;j<=n;j++){if(graph[x][j]==1&&visited[j]==false){visited[j]=true;dfs(graph,visited,j,n);}}}
}其实深搜广搜的难度并不在广搜深搜本身,而是如何应用深搜广搜去解决问题,要想明白这个逻辑。