Codeforces Round 1042 (Div. 3)

A. Lever

题目大意

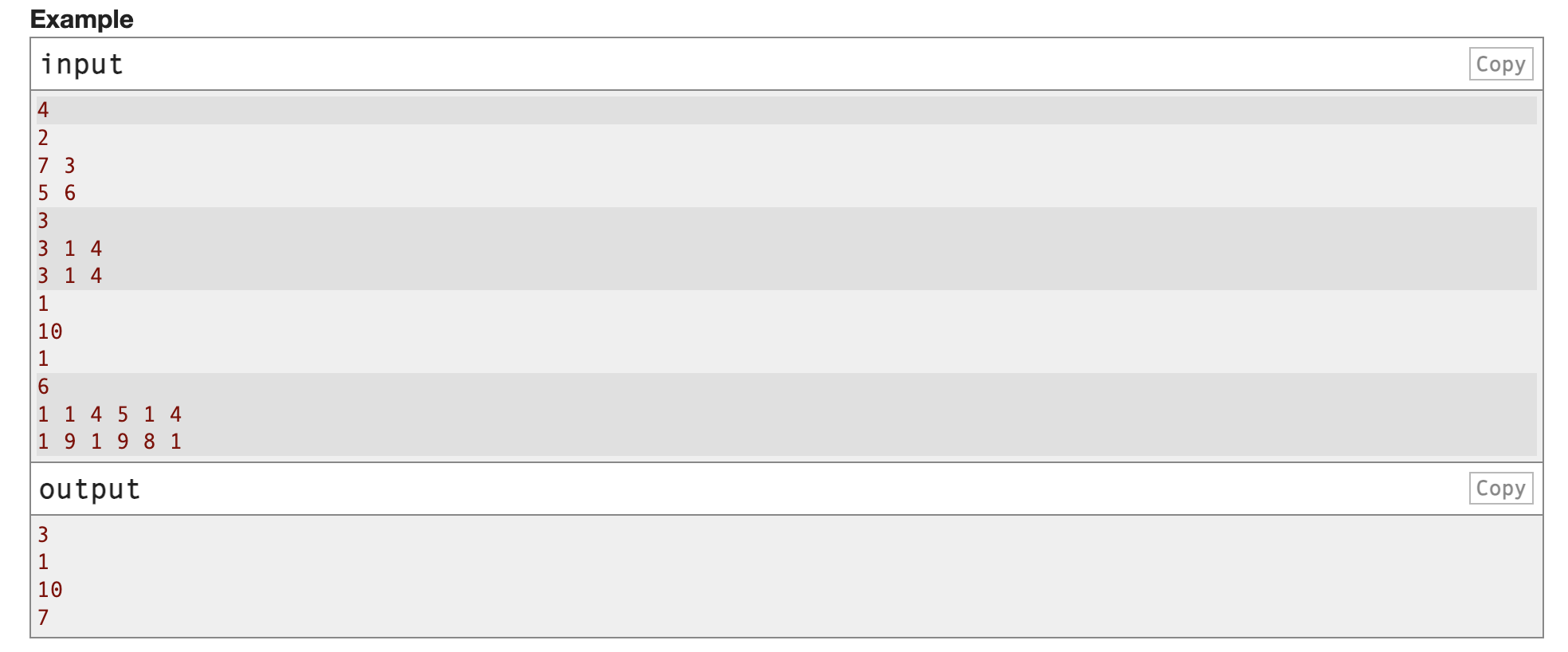
给你两个长度为n的数组a,b
在每次迭代中：
1.对于任意一个$a_i>b_i$的下标i，会让$a_i-1$
2.对于任意一个$a_i<b_i$的下标i，会让$a_i+1$
如果操作1无法执行，迭代终止
问会进行几次迭代

思路

迭代的次数为对于所有$a_i>b_i$的下标i,$a_i-b_i$的总和
操作2对操作1没有影响

// Author: zengyz
// 2025-08-13 16:55#include <bits/stdc++.h>using namespace std;
typedef long long ll;void solve()
{int n;cin >> n;vector<int> a(n), b(n);for (int i = 0; i < n; i++)cin >> a[i];for (int i = 0; i < n; i++)cin >> b[i];int cnt = 0;for (int i = 0; i < n; i++){if (a[i] > b[i])cnt += a[i] - b[i];}cout << cnt + 1 << endl;return;
}int main()
{ios::sync_with_stdio(0);cin.tie(0), cout.tie(0);int _T = 1;cin >> _T;while (_T--){solve();}return 0;
}

B. Alternating Series

题目大意

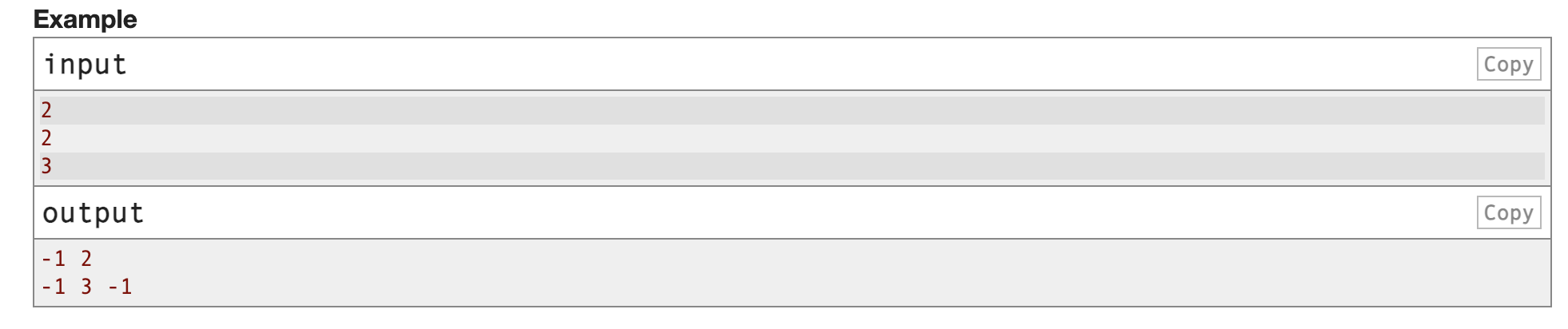
我们称一个数组是好的，当
对于任意i，有$a_i\ast a_{i+1}<0$
且任意连续子数组的和为正数
给你数组长度n，构造字典序最小的好的数组

思路

首先要求字典序最小，所以我们让负数都为-1（这样对应的正数也是最小的），然后考虑如何构造
首先对于任意i，有$a_i\ast a_{i+1}<0$，所以数组内肯定是一正一负
然后考虑样例2的情况，中间一个正数，左右两个负数，那么正数最小的情况是3
那么按-1 3 -1 3。。。的情况构造出来的一定是一个好的数组
考虑数组长度为偶数时 最后一位为2同样满足条件，且字典序更小
所以当数组为奇数时，-1 3 -1 3。。。且以-1 结尾
当数组长度为偶数时，以2结尾

// Author: zengyz
// 2025-08-13 16:58#include <bits/stdc++.h>using namespace std;
typedef long long ll;void solve()
{int n;cin >> n;if (n % 2){for (int i = 1; i <= n / 2; i++){cout << -1 << " " << 3 << " ";}cout << -1 << endl;}else{for (int i = 1; i < n / 2; i++){cout << -1 << " " << 3 << " ";}cout << -1 << " " << 2 << endl;}return;
}int main()
{ios::sync_with_stdio(0);cin.tie(0), cout.tie(0);int _T = 1;cin >> _T;while (_T--){solve();}return 0;
}

C. Make it Equal

题目大意

给你两个可重集合S，T
你可以从S中任意选择一个元素x,令x=x+k或者｜x-k |
问是否能让S和T相等

思路

令x=x+k或者｜x-k |可以变成余数为x%k或者k - (x%k)的任何数
所以我们只要逐个判断一下T中所有元素的x%k或k - (x%k)是否与S中对应即可 ，
用mp存储余数，操作S同时增加x%k或者k - (x%k)的次数
操作T同时删除x%k或者k - (x%k)的次数,如果二者都为0说明无法相等

// Author: zengyz
// 2025-08-13 17:00#include <bits/stdc++.h>using namespace std;
typedef long long ll;void solve()
{int n, k;cin >> n >> k;vector<int> s(n), t(n);map<int, int> mp;for (int i = 0; i < n; i++){cin >> s[i];mp[s[i] % k]++;mp[k-(s[i]%k)]++;}bool flag = true;for (int i = 0; i < n; i++){cin >> t[i];if (mp[t[i] % k] == 0 &&  mp[k-(t[i]%k)] == 0){flag = false;}else{mp[t[i] % k]--;mp[k-(t[i]%k)]--;}}if (flag){cout << "YES" << endl;}elsecout << "NO" << endl;return;
}int main()
{ios::sync_with_stdio(0);cin.tie(0), cout.tie(0);int _T = 1;cin >> _T;while (_T--){solve();}return 0;
}

D. Arboris Contractio

题目大意

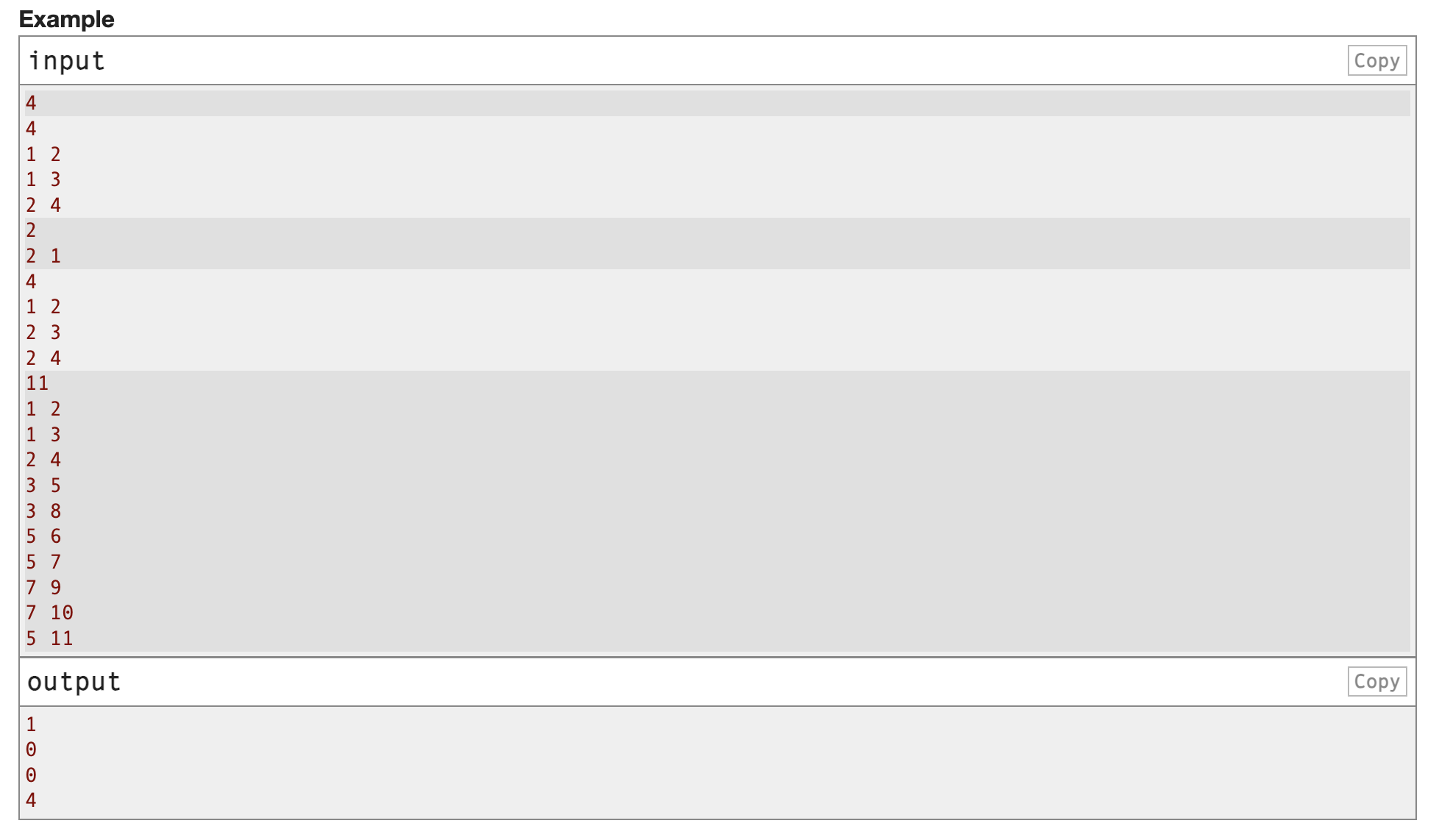
给你一棵树，你可以进行如下操作：
选择两个节点u,v
删除这两个节点之间的路径上的所有边，对于这条路径上的所有节点t
构建新的边(u,t)
问最少经过几次操作，可以使得树上任意两个节点的最短距离最小

思路

要使得任意两个节点的最短距离最小，那么这棵树一定是一棵星型的树，除一个中心结点外，其他结点都是它的叶子结点，这样任意两个节点的最短距离为2

那么我们要通过操作实现，我们就要找到一个结点t，然后对于这个结点t，将其他叶子结点和这个结点t进行操作，就可以得到这样一棵树，那么最小操作次数就是要找到这样一个t，它的子结点的叶子结点最多
我们遍历所有叶子结点的父节点并为其打上标记
找到叶子结点最多的父节点，操作次数就是总叶子结点数减去最多叶子的结点 数

// Author: zengyz
// 2025-08-13 17:21#include <bits/stdc++.h>using namespace std;
typedef long long ll;void solve()
{int n;cin >> n;vector<vector<int>> edge(n + 1);map<int, int> mp;for (int i = 1; i < n; i++){int u, v;cin >> u >> v;edge[u].push_back(v);edge[v].push_back(u);}if(n==2){cout<<0<<endl;return;}int cnt=0;for (int i = 1; i <= n; i++){if (edge[i].size() == 1){mp[edge[i][0]]++;cnt++;}}int maxx=0;for(int i=1;i<=n;i++)maxx=max(maxx,mp[i]);cout<<cnt-maxx<<endl;return;
}int main()
{ios::sync_with_stdio(0);cin.tie(0), cout.tie(0);int _T = 1;cin >> _T;while (_T--){solve();}return 0;
}

E. Adjacent XOR

题目大意

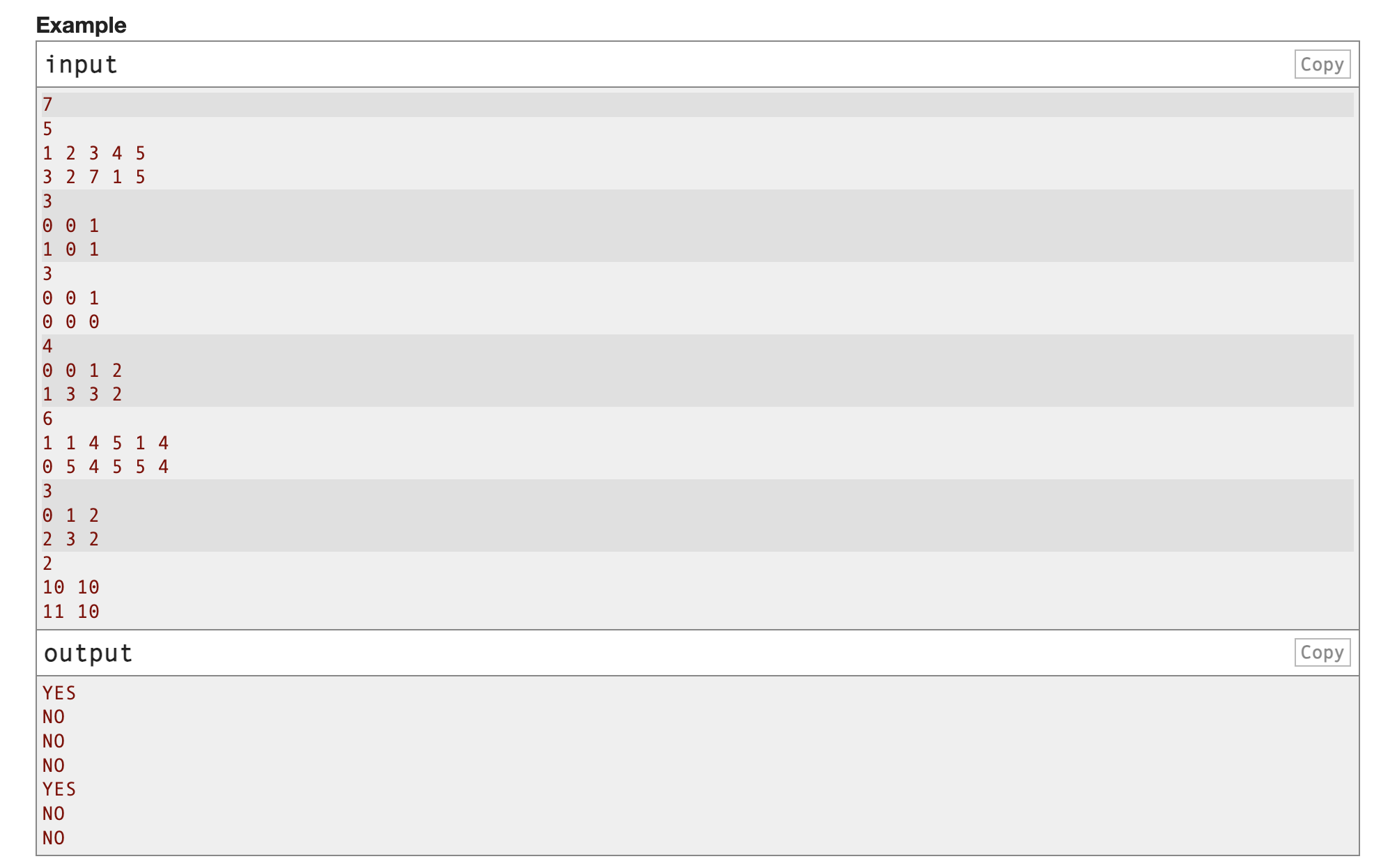
给你两个数组a,b
对于数组a的每个下标i,你可以进行至多一次操作
使得$a_i=a_i\oplus a_{i+1}$
问是否能通过操作将a变成b

思路

对于每个$a_i$
首先判断$a_i是否等于b_i$
如果不相等，那么从左到右考虑当前的i,判断$a_i\oplus a_{i+1}是否=b_i$
如果不相等，那么从右到左考虑当前的i,判断$a_i\oplus b_{i+1}是否=b_i$(因为$a_{i+1}$最后需要变成b_{i+1},我们先操作$a_{i+1}$
如果以上三种情况都不行，那么输出no
记得特判最后一个元素

// Author: zengyz
// 2025-08-13 17:29#include <bits/stdc++.h>using namespace std;
typedef long long ll;void solve()
{int n;cin >> n;vector<int> a(n), b(n);for (int i = 0; i < n; i++)cin >> a[i];for (int i = 0; i < n; i++)cin >> b[i];bool flag = true;if (a[n - 1] != b[n - 1]){cout << "NO" << endl;return;}for (int i = n - 2; i >= 0; i--){if (a[i] != b[i]){if ((a[i] ^ a[i + 1]) != b[i]){if ((a[i] ^ b[i + 1]) != b[i]){flag = false;break;}}}}if (flag){cout << "YES" << endl;}else{cout << "NO" << endl;}return;
}int main()
{ios::sync_with_stdio(0);cin.tie(0), cout.tie(0);int _T = 1;cin >> _T;while (_T--){solve();}return 0;
}