当前位置：首页 > java >正文

DAY21 常见的降维算法

java 2025/8/1 5:36:19

@浙大疏锦行

知识点回顾

1.特征降维

1.1 无监督降维 (Unsupervised Dimensionality Reduction)

定义：这类算法在降维过程中不使用任何关于数据样本的标签信息（比如类别标签、目标值等）。它们仅仅根据数据点本身的分布、方差、相关性、局部结构等特性来寻找低维表示。

输入：只有特征矩阵 X。

目标：

保留数据中尽可能多的方差（如 PCA）
保留数据的局部或全局流形结构（如 LLE, Isomap, t-SNE, UMAP）
找到能够有效重构原始数据的紧凑表示（如 Autoencoder）
找到统计上独立的成分（如 ICA）

典型算法：
PCA (Principal Component Analysis) / SVD (Singular Value Decomposition)
t-SNE (t-distributed Stochastic Neighbor Embedding)
UMAP (Uniform Manifold Approximation and Projection)
LLE (Locally Linear Embedding)
Isomap (Isometric Mapping)
Autoencoders (基本形式)
ICA (Independent Component Analysis)

1.2 有监督降维 (Supervised Dimensionality Reduction)

定义：这类算法在降维过程中会利用数据样本的标签信息（通常是类别标签 y）。它们的目标是找到一个低维子空间，在这个子空间中，不同类别的数据点能够被更好地分离开，或者说，这个低维表示更有利于后续的分类（或回归）任务。

输入：特征矩阵 X 和对应的标签向量 y。

目标：

最大化不同类别之间的可分性，同时最小化同一类别内部的离散度（如 LDA）
找到对预测目标变量 y 最有信息量的特征组合

典型算法：
LDA (Linear Discriminant Analysis)：这是最经典的监督降维算法。它寻找的投影方向能够最大化类间散度与类内散度之比。
还有一些其他的，比如 NCA (Neighbourhood Components Analysis)，但 LDA 是最主要的代表

举个例子来说明：

PCA (无监督)：如果你有一堆人脸图片，PCA会尝试找到那些能最好地概括所有人脸变化的“主脸”（特征向量），比如脸型、鼻子大小等，它不关心这些人脸属于谁。
LDA (有监督)：如果你有一堆人脸图片，并且你知道每张图片属于哪个人（标签）。LDA会尝试找到那些能最好地区分不同人的人脸特征组合。比如，如果A和B的脸型很像，但眼睛差别很大，LDA可能会更强调眼睛的特征，即使脸型方差更大。PCA是利用最大化方差来实现无监督降维，而LDA则是在此基础上，加入了类别信息，其优化目标就变成了类间差异最大化和类内差异最小化。

2.主成分分析 (PCA)

在昨天的专题中已经理解了SVD（奇异值分解），那么理解PCA（主成分分析）就会非常直接。实际上，PCA可以被看作是将SVD应用于经过均值中心化的数据矩阵，并对其结果进行特定解释的一种方法。

PCA：寻找最大方差方向

主成分分析 (PCA) 的核心思想是识别数据中方差最大的方向（即主成分）。然后，它将数据投影到由这些最重要的主成分构成的新的、维度更低子空间上。这样做的目的是在降低数据维度的同时，尽可能多地保留原始数据中的“信息”（通过方差来衡量）。新的特征（主成分）是原始特征的线性组合，并且它们之间是正交的（不相关）。

PCA 与 SVD 的关系

假设你的数据矩阵是 X（行是样本，列是特征）。

步骤 0：均值中心化 (对PCA的解释至关重要)
- 对于 X中的每一个特征（列），计算其均值。
- 从该特征列的所有值中减去这个均值。我们将这个经过均值中心化处理的矩阵称为 X_centered。
- 为什么要做这一步？ PCA的目标是找到围绕数据均值的最大方差方向。SVD本身不强制要求均值中心化，但为了将其分解结果解释为PCA的主成分，这一步是必需的。
步骤 1：对均值中心化后的数据应用 SVD
- 对 X_centered进行奇异值分解：
  
  Xcentered=U∗S∗VT
- 其中：
  - U：左奇异向量矩阵（列向量相互正交）。它的列是 Xcentered∗XcenteredT的特征向量。
  - S：奇异值矩阵（一个对角矩阵，对角线上的奇异值 s_i是非负实数，并按降序排列）。这些 s_i是 XcenteredT∗Xcentered和 Xcentered∗XcenteredT的特征值的平方根。
  - V：右奇异向量矩阵（列向量相互正交）。它的列是 XcenteredT∗Xcentered的特征向量。V的这些列向量就是主成分方向。
步骤 2：在 PCA 的语境下理解SVD的各个组成部分
- 主成分方向 (Principal Component Directions / Loadings): V矩阵的列向量（即右奇异向量）就是主成分 (PCs)。V的第一列是第一主成分（方差最大的方向），第二列是第二主成分（方差次大且与第一主成分正交的方向），以此类推。这些向量告诉你原始特征是如何线性组合形成各个主成分的。
- 解释的方差 (Variance Explained): S矩阵中的奇异值与每个对应主成分所能解释的方差量直接相关。具体来说，第 i个主成分解释的方差是 (si2)/(n−1)（其中 s_i是 S中的第 i个奇异值，n是样本数量）。更常见的是看解释方差的比例：(si2)/sum(所有sj2)。
- 主成分得分 (Principal Component Scores / Transformed Data): 如果你想将均值中心化后的数据投影到主成分上（即获得在降维后的空间中的新坐标），你可以计算：
  
  Xprojected=Xcentered∗V
  
  根据SVD的公式，这等价于：
  
  Xprojected=(U∗S∗VT)∗V=U∗S∗(VT∗V)=U∗S∗I=U∗S
  
  所以，矩阵 U * S给了你每个数据点在新的主成分轴上的“得分”。
  
  如果想将数据降至 k维，你会取 V的前 k列（记作 V_k），U的前 k列和 S的左上角 k x k部分（记作 U_k和 S_k）。
  
  降维后的数据就是 Xreduced=Xcentered∗Vk=Uk∗Sk。

PCA 何时适用？数据是线性还是非线性？

线性性:
- PCA 是一种线性降维方法。它假设主成分是原始特征的线性组合。
- 它寻找的是一个能够最好地捕捉数据方差的线性子空间。
- 如果你的数据的潜在结构是高度非线性的（例如，“瑞士卷”形状、螺旋形），PCA可能无法有效地在低维空间中捕捉这种结构。它可能会将这类结构“压平”或扭曲。
PCA 效果好的情况:
- 目标是最大化方差: 当你认为数据中方差最大的方向包含了最重要的信息时。这在去噪或特征间存在相关性时通常是成立的。
- 数据分布大致呈椭球形或存在线性相关性: PCA 擅长找到这类分布的主轴。
- 作为其他线性模型的预处理步骤: 不相关的主成分有时能让线性模型（如逻辑回归、线性SVM）表现更好。
- 探索性数据分析 (EDA): 快速了解数据变异的主要模式。
- 降噪: 假设噪声的方差低于信号的方差，PCA可以通过舍弃低方差的成分来帮助降噪。
- 当原始特征数量非常多，且存在多重共线性时：PCA可以通过生成少数几个不相关的主成分来解决多重共线性问题，并减少特征数量。
PCA 可能不适用或需要谨慎使用的情况:
- 高度非线性数据: 对于分布在复杂流形上的数据（例如“瑞士卷”、“S型曲线”），PCA会将其投影到一个线性子空间，这可能会丢失关键的非线性关系。在这种情况下，非线性降维技术（如 t-SNE, UMAP, LLE, Isomap, 核PCA, 自编码器）会是更好的选择。
- 方差并非衡量重要性的唯一标准: 有时，方差较小的方向可能对特定任务至关重要（例如，在分类问题中，如果使用LDA，一个整体方差较小的方向可能对区分类别非常有效）。PCA是无监督的，它不考虑类别标签。
- 主成分的可解释性: 虽然主成分是原始特征的线性组合，但与保留原始、可解释的特征相比，它们的直接物理解释有时可能更具挑战性。
- 数据特征尺度差异巨大: 如果特征的尺度（单位或数值范围）相差悬殊（例如，一个特征以米为单位，另一个以毫米为单位），那么尺度较大的特征将在方差计算中占据主导地位，从而主导第一主成分。这就是为什么在应用PCA之前几乎总是推荐进行数据标准化（例如，将特征缩放到均值为0，方差为1）。

总而言之，可以将PCA视为：

对数据进行均值中心化。
对中心化后的数据进行SVD。
使用SVD得到的右奇异向量 V作为主成分方向。
使用奇异值 S来评估每个主成分的重要性（解释的方差）。
使用 U*S（或 X_centered * V）来获得降维后的数据表示。

PCA主要适用于那些你认为最重要的信息可以通过数据方差来捕获，并且数据结构主要是线性的情况。

3.t-分布随机邻域嵌入 (t-SNE)

保持高维数据的局部邻域结构，用于可视化

PCA 的目标是保留数据的全局方差，而 t-SNE 的核心目标是在高维空间中相似的数据点，在降维后的低维空间中也应该保持相似（即彼此靠近），而不相似的点则应该相距较远。 它特别擅长于将高维数据集投影到二维或三维空间进行可视化，从而揭示数据中的簇结构或流形结构。

t-SNE 与 PCA/SVD 的主要差异：

特性	PCA/SVD	t-SNE
类型	线性	非线性
主要目标	保留全局方差	保留局部邻域结构，用于可视化
关注点	全局结构	局部结构，尽可能在低维呈现高维的邻近关系
计算成本	相对较低	较高，尤其是对于大数据集
输出稳定性	确定性（给定数据，结果唯一）	随机性（优化过程通常有随机初始化，多次运行结果可能略有不同）
超参数	`n_components`	`perplexity`(困惑度), `n_iter`(迭代次数), `learning_rate`等
全局结构保留	较好（因为它关注方差）	可能较差，t-SNE 更关注保持局部结构，可能扭曲全局距离
降维后坐标含义	主成分有明确的方差含义	坐标本身没有直接的物理意义，点之间的相对距离和簇的形状更重要
适用场景	通用降维，去噪，数据压缩，线性模型预处理	高维数据可视化，探索数据中的簇或流形结构

何时适合使用 t-SNE？

当你主要目的是可视化高维数据时：t-SNE 在将复杂的高维数据结构展现在2D或3D图上时非常强大，能帮助你直观地看到数据中可能存在的簇或模式。
当数据具有复杂的非线性结构时：如果数据分布在一个弯曲的流形上，t-SNE 比 PCA 更能捕捉到这种结构。
探索性数据分析：帮助发现数据中未知的群体。

使用 t-SNE 时需要注意的事项：

计算成本高：对于非常大的数据集（例如几十万甚至上百万样本），t-SNE 的计算会非常慢。通常建议在应用 t-SNE 之前，先用 PCA 将数据降到一个适中的维度（例如50维），这样可以显著加速 t-SNE 的计算并可能改善结果。
超参数敏感：
- Perplexity (困惑度)：这个参数对结果影响较大。常见的取值范围是 5 到 50。较小的困惑度关注非常局部的结构，较大的困惑度则考虑更广泛的邻域。通常需要尝试不同的值。
- n_iter (迭代次数)：需要足够的迭代次数让算法收敛。默认值通常是1000。如果可视化结果看起来还不稳定，可以尝试增加迭代次数。
- learning_rate (学习率)：也可能影响收敛。
结果的解释：
- 簇的大小和密度在 t-SNE 图中没有直接意义。t-SNE 会尝试将所有簇展开到相似的密度。不要根据簇在图上的大小来判断原始数据中簇的实际大小或密度。
- 点之间的距离在全局上没有意义。两个相距较远的簇，它们之间的距离并不代表它们在原始高维空间中的实际距离。t-SNE 主要保留的是局部邻域关系。
- 多次运行结果可能不同：由于优化过程的随机初始化和梯度下降的性质，多次运行 t-SNE 可能会得到略微不同的可视化结果。但好的簇结构通常是稳定的。
不适合作为通用的有监督学习预处理步骤：因为它的目标是可视化和保持局部结构，而不是最大化类别可分性或保留全局方差，所以它通常不直接用于提高分类器性能的降维。LDA 或 PCA (在某些情况下) 更适合这个目的。

总结一下：

t-SNE 是一种强大的非线性降维技术，主要用于高维数据的可视化。它通过在低维空间中保持高维空间中数据点之间的局部相似性（邻域关系）来工作。与PCA关注全局方差不同，t-SNE 更关注局部细节。理解它的超参数（尤其是困惑度）和结果的正确解读方式非常重要。

4.线性判别分析 (Linear Discriminant Analysis, LDA)

1. 核心定义与目标：

线性判别分析 (LDA) 是一种经典的有监督降维算法，也常直接用作分类器。作为降维技术时，其核心目标是找到一个低维特征子空间（即原始特征的线性组合），使得在该子空间中，不同类别的数据点尽可能地分开（类间距离最大化），而同一类别的数据点尽可能地聚集（类内方差最小化）。

2. 工作原理简述：

LDA 通过最大化"类间散布矩阵"与"类内散布矩阵"之比的某种度量（例如它们的行列式之比）来实现其降维目标。它寻找能够最好地区分已定义类别的投影方向。

3. 关键特性：

有监督性 (Supervised): 这是 LDA 与 PCA 最根本的区别。LDA 在降维过程中必须使用数据的类别标签 (y) 来指导投影方向的选择，目的是优化类别的可分离性。
降维目标维度 (Number of Components): LDA 降维后的维度有一个严格的上限：min(n_features, n_classes - 1)。
- n_features：原始特征的数量。
- n_classes：类别标签 (y) 中不同类别的数量。
线性变换 (Linear Transformation): 与 PCA 类似，LDA 也是一种线性方法。
数据假设 (Assumptions):
- 理论上，LDA 假设每个类别的数据服从多元高斯分布。
- 理论上，LDA 假设所有类别具有相同的协方差矩阵。

4. 输入要求：

特征 (X): 数值型特征。
标签 (y): 一维的、代表类别身份的数组或 Series。

5. 与特征 (X) 和标签 (y) 的关系：

LDA 的降维过程和结果直接由标签 y中的类别结构驱动。
原始特征 X提供了构建这些判别特征的原材料。

6. 优点：

直接优化类别可分性
计算相对高效
生成的低维特征具有明确的判别意义

7. 局限性与注意事项：

降维的维度受限于 n_classes - 1
作为线性方法，可能无法捕捉数据中非线性的类别结构
对数据的高斯分布和等协方差假设在理论上是存在的
如果类别在原始特征空间中本身就高度重叠，LDA 的区分能力也会受限

8. 适用场景：

当目标是提高后续分类模型的性能时
当类别信息已知且被认为是区分数据的主要因素时
当希望获得具有良好类别区分性的低维表示时

简而言之，LDA 是一种利用类别标签信息来寻找最佳类别分离投影的降维方法，其降维的潜力直接与类别数量挂钩。

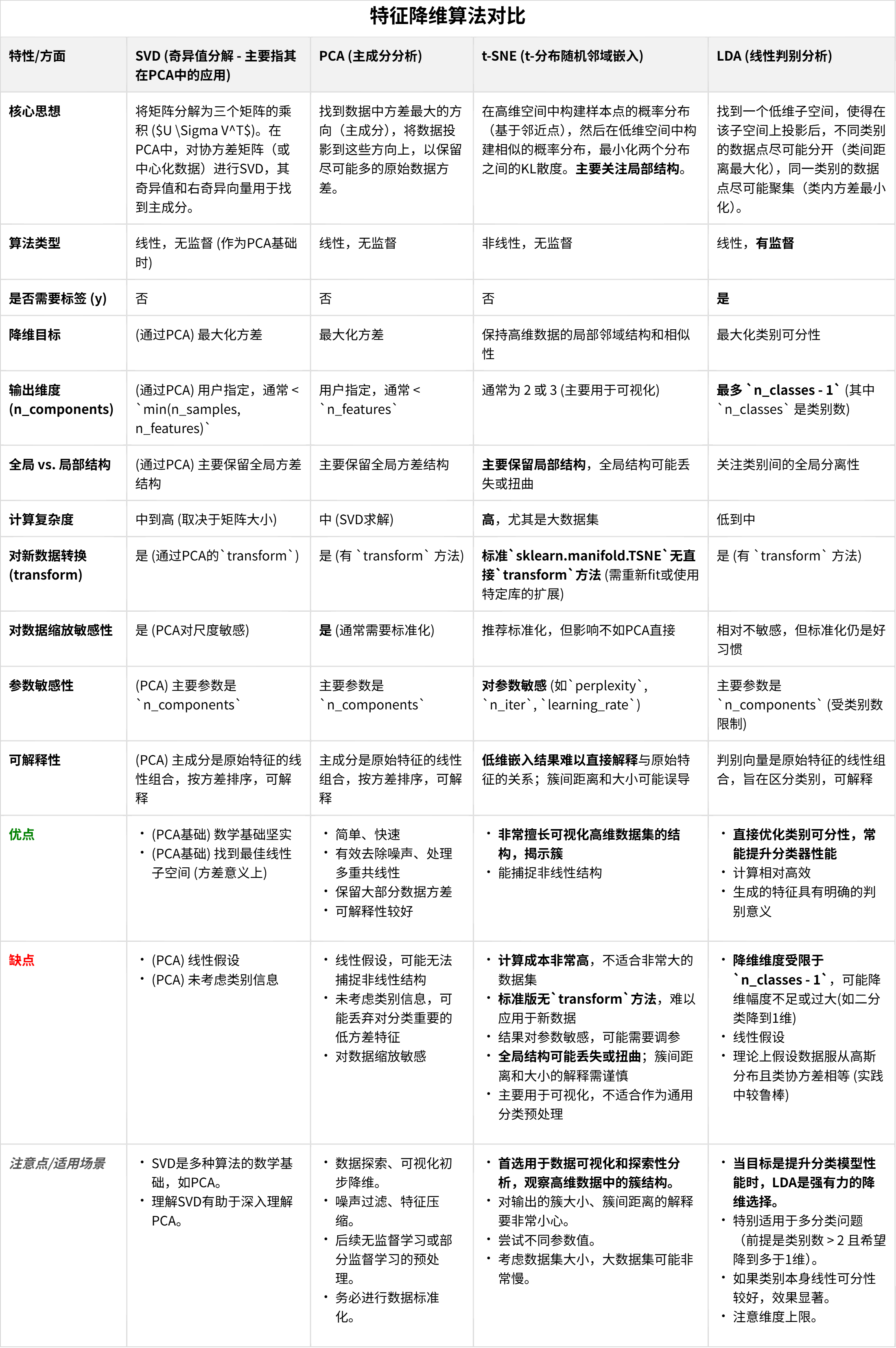
作业：

自由作业：探索下什么时候用到降维？降维的主要应用？或者让ai给你出题，群里的同学互相学习下。可以考虑对比下在某些特定数据集上t-sne的可视化和pca可视化的区别。

降维技术的主要应用场景

一、数据可视化（最常用场景）

高维数据可视化：将数十/数百维数据降至2D/3D进行可视化
- 常用算法：t-SNE、UMAP、PCA
- 典型应用：基因表达数据可视化、客户分群展示
探索性数据分析(EDA)：通过降维发现数据中的潜在模式
- 示例：通过PCA主成分分析发现数据的主要变异方向

二、机器学习模型优化

特征工程：
- 解决"维度灾难"（特征数>>样本数）
- 消除特征间多重共线性
- 常用方法：PCA、LDA、因子分析
模型加速：
- 减少训练时间（特别是对SVM、KNN等计算密集型算法）
- 降低存储需求
提升模型表现：
- 去除噪声和非信息特征
- 增强特征判别力（如LDA）

三、特定领域应用

图像处理：
- 人脸识别（Eigenfaces）
- 图像压缩（JPEG基于类似PCA的变换）
自然语言处理：
- 词向量降维（Word2Vec/PCA）
- 主题建模（LSA/LDA）
生物信息学：
- 基因表达数据分析
- 蛋白质结构研究
金融分析：
- 投资组合优化
- 风险因子分析

四、数据压缩与去噪

数据压缩：
- 保留90%+信息的同时大幅减少存储空间
- 示例：将1000维数据降至50维
信号去噪：
- 通过保留主要成分去除随机噪声
- 应用：EEG/ECG信号处理

五、异常检测

基于重构误差：
- 高维数据降维后尝试重构
- 重构误差大的样本可能是异常值
低维空间检测：
- 在降维后的空间更容易发现异常点

何时需要使用降维？

当特征维度>50时：考虑使用线性降维(PCA等)
当特征间高度相关时：用PCA消除相关性
当需要可视化高维数据时：t-SNE/UMAP
当样本量<特征量时：避免过拟合
当计算资源有限时：加速模型训练
当需要去除数据噪声时：保留主要成分

不同场景的算法选择指南

应用场景	推荐算法	备注
数据可视化	t-SNE, UMAP	保持局部结构
监督学习预处理	PCA, LDA	LDA需要标签
非结构化数据	自编码器	图像/文本等
实时系统	随机投影	计算效率高
线性数据结构	PCA	全局结构保持
流形学习	LLE, Isomap	非线性结构