再论自然数全加和-4

对于参数s为任意值的情况，同样令，

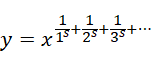
两边取对数，

对 求（偏）导，

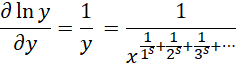
这种形式在，

时成立，所以用1替换 ，

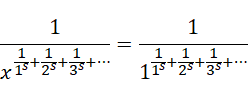
得到，

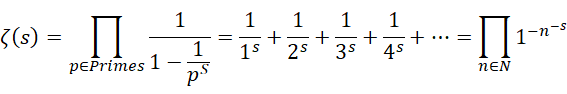
也就是，

用语言描述来说，它就是基本虚数单位 的 次幂。等号的左边乘以某个数，右边将1替换为 ，可以得到，

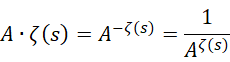
于是可以认为， 是一种算子，将其作用于数量 ，就可以求出以 为单位的基本虚数单位旋转 次之后的结果。这里的旋转类比于对虚数单位 的旋转，但差别是，虚数单位的旋转，是对于数量的外化旋转，

其中-1的大小是与 无关的。但是 的旋转，指的是以 为单位，也就是说-1或者1的大小就是 决定的，

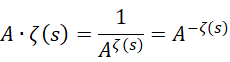
而且这个过程可以无限延展下去，

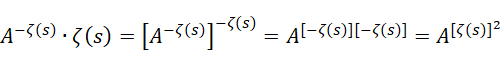
因为指数的正负随着迭代的次数来回反转，所以会不断的出现，

也就是正的或者负的幂次。我们可以认为这个过程是膨胀和收缩不断交替的过程。而且这两个过程可以同时进行，也就是说，一个不断膨胀，一个不断收缩，同时发生，甚至同时翻转。这里的s，也可以认为是一种自旋，配合n一起则意味着时间的演进。

我们知道所谓全体自然数是不可知的，因为观察者自身的有限性，所以最多只能认识到有限的自然数。但是质数模式和加一模式配合起来就可以扩展可认知的数量空间，也就是说可以帮助系统发现新的更大的数。如果一个更大的质数被找到， 就可以扩展出一个新的序列段，此时的 就不同于原来的 ，这就导致了 的自增。此后 会更大，它的倒数会更小，出现向着两端分化的效果。