6.1.1图的基本概念

基本概念

图：

顶点集+边集

顶点集：所有顶点的集合，不能为空（因为图是顶点集和边集组成，其中一个顶点集不能为空，则图肯定不为空）

边集：所有边的集合，边是由顶点集中的2个顶点构成，如果边集里的边不是由顶点集里的2个顶点构成，那就构不成图，可以为空

无向图：

（只有度、边、连通、连通图、极大连通子图(连通分量)、生成树、带权路径长度的概念）

各个边没有方向，A和B有一条线，则A可以到B，B可以导A。边用圆括号()，（A，B）=（B，A）

度：

依附于该顶点的边的条数，也就是这个顶点有多少条线。记为TD(V)。TD(C)=2。一条边为2个顶点提供一个度，即无向图的度数之和是边数的2倍

有向图：

（只有入度、出度、弧头、弧尾，强连通、强连通图、强连通分量概念）：

各个边有方向，各个边又称为弧，用尖括号<>表示边，<A,B>≠<B,A>，A指向B，B没有指向A，则B就不能到A。有箭头指向的顶点称为弧头，没有箭头指向的顶点称为弧尾，如<v,w>是从v到w的距离，v指向w，w是是弧头，v是弧尾

顶点的入度：

以该顶点为基准，往该顶点指的箭头有几个。有多少边指向该顶点。ID(A)=1

顶点的出度：

以该顶点为基准，往外指的箭头有几个。该顶点指向多少边。OD(A)=4

 简单图：没有顶点到自身的边+没有重复边

多重图：加了顶点到自身的边

路径(2个顶点之间)：

从1个顶点到另外一个顶点经过了哪些顶点序列（顶点可以重复，没有重复的顶点序列就是简单路径)。

距离(2个顶点之间)：

路径的长度。估摸是路径中的顶点序列个数

无向图A到D的路径：ABD顶点序列(简单路径)或ABED(简单路径)序列或ABECD(简单路径)序列或ABEBD（出现重复顶点B，不是简单路径，但还是路径）即顶点序列

无向图连通(2个顶点之间)：

从一个顶点到另外一个顶点之间有没有路径存在，有路径就是连通，没路径就是不连通。F顶点没边，即和其他顶点没有连接，没有路径，不连通，没有路径的距离都是∞，距离都是最短序列（没边的顶点都没有路径，没有路径的距离都是∞）

有向图强连通(2个顶点之间)：

如果从A到E有路径，从E到A有路径，则称为两个顶点强连通。如果有向图A到E有路径，E到A没有路径，因为没有从E指出的箭头，

连通图：

针对无向图来说，任意2个顶点都是连通的，即都有路径，称为连通图，否则称为非连通图。

强连通图：

针对有向图来说，任意2个顶点都是强连通的，就是强连通图

子图：

从一个图的顶点集合拿出一些顶点，再从图的边集里拿出一些边，拿出的边集和顶点集构成的图（一定要构成图，有的还构不成图，如下图就够不成图）就是原图的子图

生成子图：

有2个图，图A和图B，图A和图B的顶点集完全相同，但是图B的边集比图A的边集少（即少几条边）那图B就是图A的生成子图 

 

连通分量（极大，无向图）：

极大连通子图（无向图的子图中的任意2个顶点之间都是连通的，即有路径，并且尽可能都多的顶点和边)称为连通分量

连通分量如下：无向图中G的三个子图中都是连通图(任意2个顶点之间都有路径，子图G只有一个顶点没边，所以认为也是连通的吧，各个子图带多个顶点啥的就不是连通图了，比如把J这个顶点放到GHI这个子图里，GHI子图就不连通了)，且尽可能多的包含了无向图G中的顶点和边（那意思是无向图G原来不是连通图吧，因为J这个顶点和任意顶点都不连通且G、I、H和带A的子图也不连通）

 强连通分量（有向图）：

有向图中的ABCDE顶点是强连通的(因为各个顶点之间可以逆推)，但是加上F顶点不是(因为ABCDE顶点都可以推到F顶点，即连通，但是F顶点没有到ABCDE的箭头指向，即没有路径不能逆推，故不是强联通的)，所以要把F顶点抽离出来，G顶点同，故构成如下三个强联通子图即强连通分量（跟无向图类似，还是让每个子图尽量有多的可强连通的顶点和边）

生成树（极小）：

针对无向图来说，首先生成树包含图中的所有顶点还要保持连通，但是还要在连通的请情况下保证边少，即在保证连通的情况下，顶点数-1为最少的边数，因为少一条边的树有各种形式，则一个图的生成树可能有多条。对于生成树而言，少一条边就会变成非连通图，多一条边就会形成一个回路。

一般生成树用于各个没有打通的村修路，各个村就相当于各个顶点，要让各个村打通，不一定要把各个村之间都修上路，因为花费太大，所以可以使用生成树的概念，在保证各个村连通的前提下，有最少的边，边修少了意味着修路的花费变少，且因为一个图的生成树样式不只一种，则可以根据现实中修每条路的实际成本有多少，来确定到底怎样修路

 

生成森林：

顺序是图是非连通图，然后形成一个个连通分量(各个连通分量都是连通的且是图的极大连通子图，即在保证连通的前提下，每个连通分量拥有尽可能多的图的顶点和边)，然后连通分量再形成生成树(生成树都是连通的，且生成树拥有连通分量的全部顶点和在保证连通的前提下尽可能少的边)，然后就形成了生成森林（估摸是所有的连通分量的生成树合在一起叫生成森林吧）

 

带权路径长度：

给路径标上值，从北京到上海的带权路径长度=经过的路径上标的值之和

带权图：

给路径上标值的图

 

 

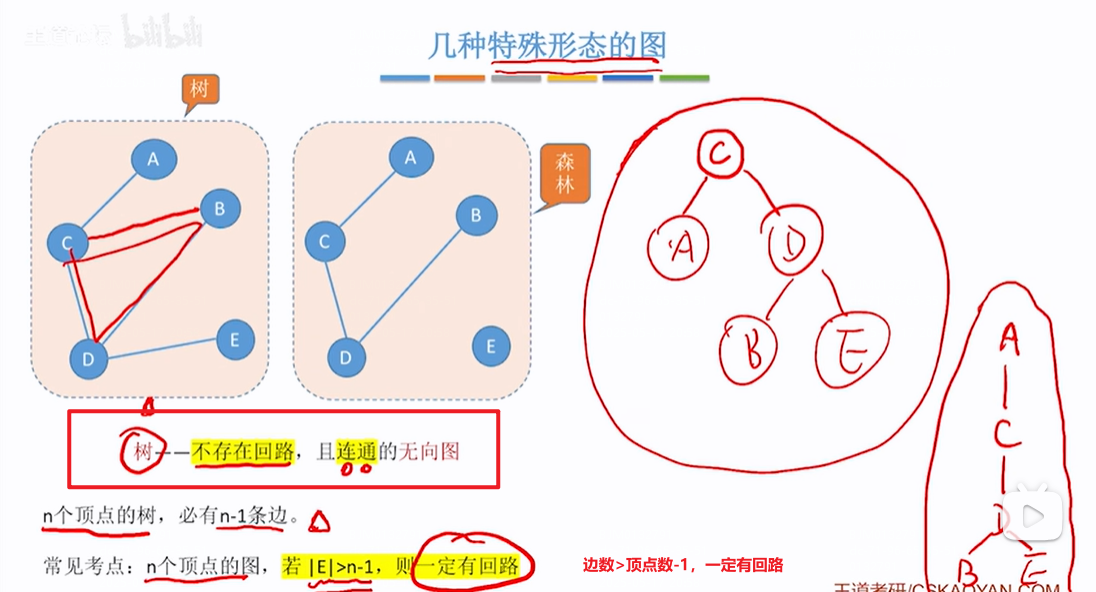
有向树并不是强连通图，不是不都是是不是强连通图 

 

做个记录。。。。。。