Rotary Positional Embedding

先介绍几个之前的PE：

1. Absolute Positional Embedding

比如 Transformer原论文中的PE。

问题：理论上讲，位置1，2对应的PE应该在距离上比位置1，500的PE更接近，但APE做不到这一点。

2.Relative Positional Embedding

解决了APE中的问题，但也带来了计算效率低下等问题。此处不对RPE做详细介绍

3.Learned Positional Embedding

每个位置的PE通过学习得到。

问题：如果训练集中的Sequence Length都是512以内，那么当推理时遇到长度长于512得到sequence时，就会出问题了。

4.Rotary Positional Embedding

不太懂旋转矩阵的可以参考这个链接

RoPE怎么做的？请看：

当embedding维度为2时，position的位置每往后一个，就把embedding对应维度旋转θ角度，这就是RoPE的核心思想。

再看论文的公式13：

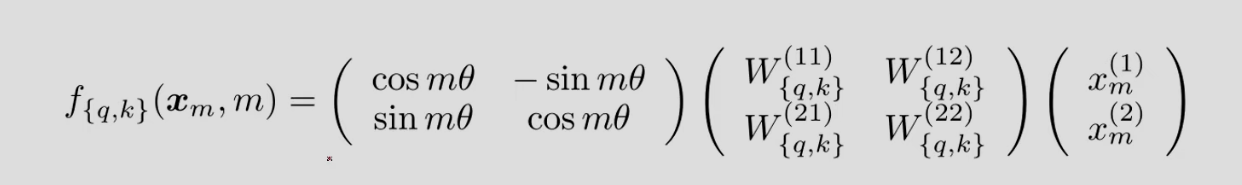
其中$x_m$表示位置$m$处的embedding（由embedding层得到，还不含PE信息）； { q , k } \{q,k\} {q,k}表示得到的是$q$或者$k$的表示（不含$v$）。

矩阵乘法的后两项，就是把二维的embedding映射到$q$和$k$的简单映射（四个W都是标量）。这里的操作和Attention Is All You Need中得到$q$或者$k$的操作是完全一样的（如果去掉Attention Is All You Need中的PE的话）。

而矩阵的第一项，就是把矩阵做一个简单的旋转，这一点我们已经提到过了。

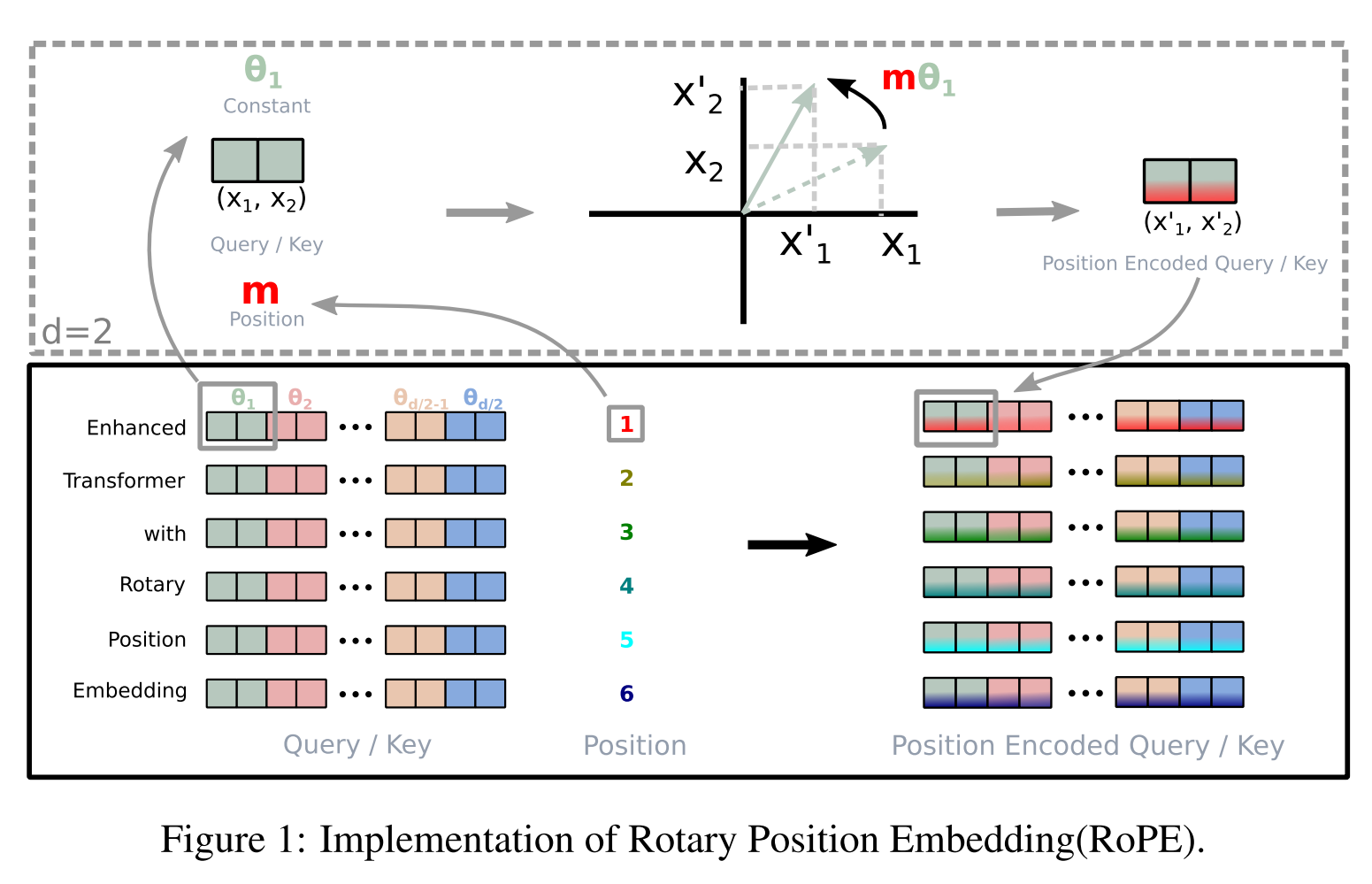
当embedding维度大于2的时候怎么办呢？我们只需要将维度2个2个地进行旋转就行了：

原始论文也对这一过程进行了图解说明：

参考链接

参考链接1
参考链接2
参考链接3