高中数学联赛模拟试题精选学数学系列第7套几何题
点 O O O 和点 I I I 分别是 △ A B C \triangle ABC △ABC 的外心和内心. 点 A A A 关于 I I I 的对称点为点 K K K, 点 K K K 关于 B C BC BC 的对称点为点 L L L. 求证: △ A O I ∼ △ I O L \triangle AOI \sim \triangle IOL △AOI∼△IOL. (《高中数学联赛模拟试题精选》“学数学”系列第7套几何题)

证明:
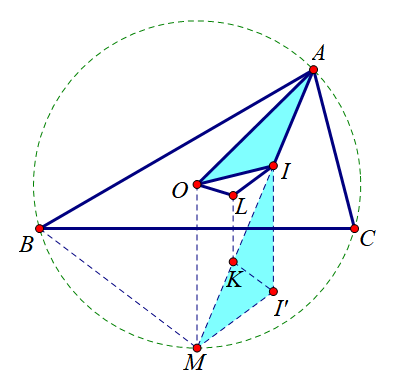
设 I I I 关于直线 B C BC BC 的对称点为点 I ′ I' I′. 延长 A I AI AI 交 ( A B C ) (ABC) (ABC) 于点 M M M. 设 △ A B C \triangle ABC △ABC 的外接圆半径和内切圆半径分别为 R R R, r r r.
首先证明: △ O A I ∼ △ M I I ′ \triangle OAI \sim \triangle MII' △OAI∼△MII′.
∠ O A I = ∠ M I I ′ = ∣ π 2 − ( B + A 2 ) ∣ \angle OAI=\angle MII'=|\frac{\pi}{2}-(B+\frac{A}{2})| ∠OAI=∠MII′=∣2π−(B+2A)∣.
只需证明 M I / O A = I I ′ / A I MI/OA=II'/AI MI/OA=II′/AI.
由鸡爪定理 M I = M B = 2 R sin A 2 MI=MB=2R\sin \frac{A}{2} MI=MB=2Rsin2A.
M I / O A = 2 sin A 2 MI/OA=2\sin \frac{A}{2} MI/OA=2sin2A.
显然 I I ′ / A I = 2 r A I = 2 sin A 2 II'/AI=\frac{2 r}{AI}=2\sin \frac{A}{2} II′/AI=AI2r=2sin2A.
所以 △ O A I ∼ △ M I I ′ \triangle OAI \sim \triangle MII' △OAI∼△MII′.

再证明: △ I O M ∼ △ I ′ K I \triangle IOM \sim \triangle I'KI △IOM∼△I′KI.
显然 O I / / I I ′ OI//II' OI//II′, 所以 ∠ O M I = ∠ K I I ′ \angle OMI=\angle KII' ∠OMI=∠KII′.
I M / O M = 2 sin A 2 IM/OM=2\sin \frac{A}{2} IM/OM=2sin2A, I I ′ / K I = 2 r A I = 2 sin A 2 II'/KI=\frac{2r}{AI}=2\sin \frac{A}{2} II′/KI=AI2r=2sin2A.
所以 △ I O M ∼ △ I ′ K I \triangle IOM \sim \triangle I'KI △IOM∼△I′KI.
最后证明: △ O I L ∼ △ M I I ′ \triangle OIL \sim \triangle MII' △OIL∼△MII′.
∠ O I M = ∠ K I ′ I \angle OIM=\angle KI'I ∠OIM=∠KI′I.
显然四边形 L I I ′ K LII'K LII′K 是等腰梯形, 所以 ∠ L I I ′ = ∠ K I ′ I \angle LII'=\angle KI'I ∠LII′=∠KI′I 且 L I = K I ′ LI=KI' LI=KI′.
所以 ∠ O I M = ∠ L I I ′ \angle OIM=\angle LII' ∠OIM=∠LII′, 进而 ∠ O I L = ∠ M I I ′ \angle OIL=\angle MII' ∠OIL=∠MII′.
I O / I L = I O / K I ′ = I M / I I ′ IO/IL=IO/KI'=IM/II' IO/IL=IO/KI′=IM/II′.
所以 △ O I L ∼ △ M I I ′ \triangle OIL \sim \triangle MII' △OIL∼△MII′.
由相似关系的传递性可知 △ A O I ∼ △ I O L \triangle AOI \sim \triangle IOL △AOI∼△IOL.
证毕.
