Day21_【机器学习—决策树(1)—信息增益、信息增益率、基尼系数】
一、决策树简介
| 名称 | 提出时间 | 分支方式 | 特点 |
|---|---|---|---|
| ID3 | 1975 | 信息增益 | 1.ID3只能对离散属性的数据集构成决策树 2.倾向于选择取值较多的属性 |
| C4.5 | 1993 | 信息增益率 | 1.缓解了ID3分支过程中总喜欢偏向选择值较多的属性 2.可处理连续数值型属性,也增加了对缺失值的处理方法 3.只适合于能够驻留于内存的数据集,大数据集无能为力 |
| CART | 1984 | 基尼指数 | 1.可以进行分类和回归,可处理离散属性,也可以处理连续属性 2.采用基尼指数,计算量减小 3.一定是二叉树 |
1. 概念
决策树是一种树形结构,是一种常用的机器学习算法,用于分类和回归任务
核心思想:通过一系列“问题”(通常是基于特征的阈值判断)来将数据逐步划分,最终得到预测结果
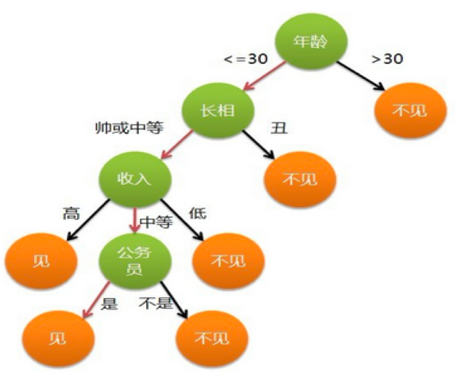
每个叶子节点代表一种分类结果(标签)
每个中间节点表示一个特征
第一层第二层分类效果更好
决策树也易过拟合,采用剪枝的方法缓解过拟合
2. 建立过程
1. 特征选择
这是决策树构建的第一步,目的是从所有特征中选择一个最优特征来划分数据集。选择标准通常基于信息增益、信息增益率或基尼指数等指标。
- 信息增益(Information Gain):基于信息熵的概念,选择使子集纯度提升最大的特征。
- 信息增益率(Gain Ratio):对信息增益进行归一化处理,避免偏向取值较多的特征。
- 基尼指数(Gini Index):衡量数据的不纯度,选择使基尼指数最小的特征进行划分。
2. 决策树生成
从根节点开始,递归地对数据集进行划分:
- 根节点:包含全部训练数据。
- 内部节点:根据选定的特征和划分标准,将数据分割到不同的子节点。
- 叶节点:当满足停止条件时,生成叶节点,代表最终的分类或回归结果。
每次划分后,对每个子集重复上述过程,直到满足停止条件。
3. 停止条件
为了避免过拟合,需要设定停止条件,常见的有:
- 当前节点中的样本全部属于同一类别。
- 没有更多特征可用于划分。
- 树的深度达到预设的最大值。
- 节点中的样本数少于预设阈值。
- 信息增益或基尼指数改善小于某个阈值。
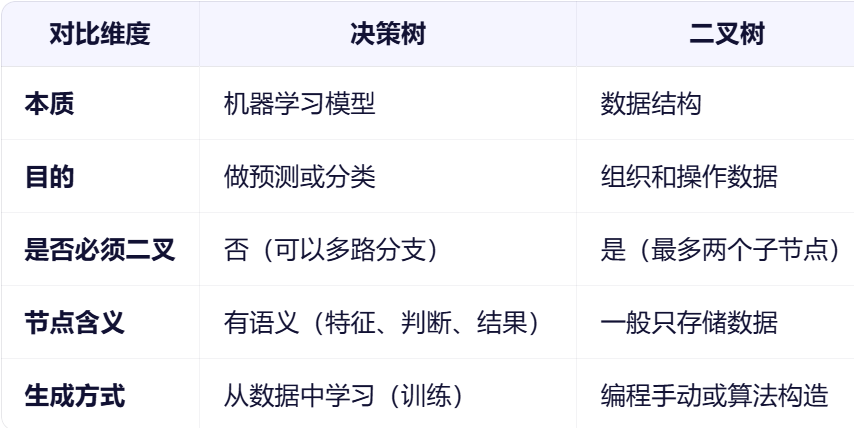
3. 决策树不是二叉树
二、各种熵
1. 信息熵
概念
- 信息熵 :是信息论中的核心概念,由克劳德·香农(Claude Shannon)在1948年提出,用于量化信息的不确定性或信息量。
- 熵越大,数据的不确定性度越高,信息就越多
- 熵越小,数据的不确定性越低
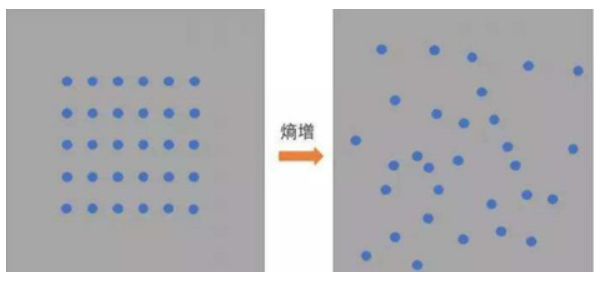
熵越大,数据越混乱,所以数据从有序向无序变化过程其实就是熵增大得过程 熵增
公式


,可以理解为是各标签的比例,
(标签列的各个不同种类的数量/标签总数量 * log2 标签列的各个不同种类的数量/标签总数量)再求和
2. 条件熵
概念
条件熵(Conditional Entropy)是信息论中的一个概念,用于衡量在已知一个随机变量的情况下,另一个随机变量的不确定性。
公式
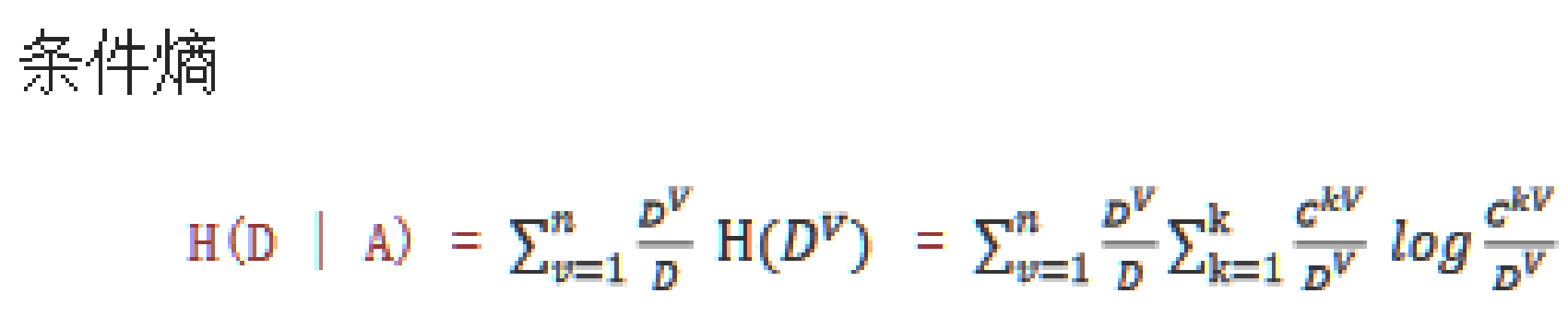
白话的说:在已知一种特征的条件下,求它的信息熵
公式:该特征数量/总特征数量 * 该特征的信息熵,这是一个特征的条件熵,算总的条件熵需要在此基础上求和计算
信息熵与条件熵的小案例

3. 特征熵
概念
也叫分裂信息量, 衡量的是一个特征本身取值的混乱程度或不确定性
公式
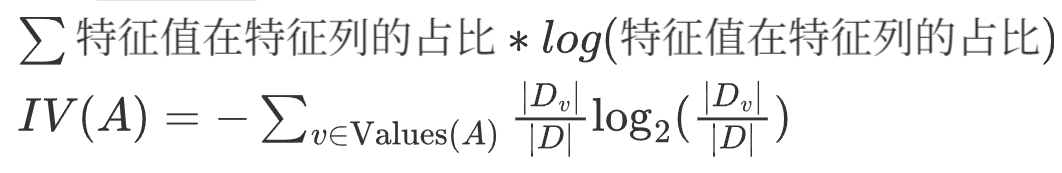
4.信息增益
信息增益(Information Gain,简称 IG)是信息论和机器学习中衡量一个特征对分类任务“信息量”大小的指标,也是决策树算法(如 ID3、C4.5)选择最佳划分属性的核心依据。
信息增益衡量的是,由于特征A而使得对数据D的分类不确定性减少的程度。
公式

5.信息增益率
相当于对信息增益进行修正,增加一个惩罚系数
公式

![]()
6.基尼指数
基尼值 (Gini)
定义
从数据集 D 中随机抽取两个样本,这两个样本的类别标记不一致的概率
Gini(D) 越小,说明数据集中同类样本越多,纯度越高;
Gini(D) 越大,说明数据集中类别混杂,纯度越低。
公式

基尼指数(Gini index)
定义
用某个属性 a 对数据集 D 进行划分后,得到的“加权平均基尼值”,用来衡量这个属性划分的好坏。
公式
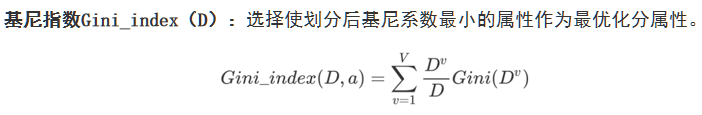
Gini_index(D, a) 越小,说明用属性 a 划分后,子集纯度越高,这个属性越适合作为划分依据。
基尼指数小案例