代码随想录二刷之“回溯”~GO
组合问题
剪枝精髓是:for循环在寻找起点的时候要有一个范围,如果这个起点到集合终止之间的元素已经不够题目要求的k个元素了,就没有必要搜索了。
1.77. 组合 - 力扣(LeetCode)
没减枝前:这里传start,不走回头路。我第一次写的时候传了path数组,略麻烦/
func combine(n int, k int) [][]int {res := [][]int{}path := []int{}var travel func(n int,k int,start int)travel = func(n int,k int ,start int){if len(path) == k{tempCopy := make([]int,k)copy(tempCopy,path)res = append(res,tempCopy)return }for i := start;i <= n;i++{path = append(path,i)travel(n,k,i+1)path = path[:len(path)-1]}}travel(n,k,1)return res
}
减枝1: if n - start + 1 < k -len(path) { break }for循环选择的起始位置之后的元素个数 已经不足 我们需要的元素个数了,那么就没有必要搜索了
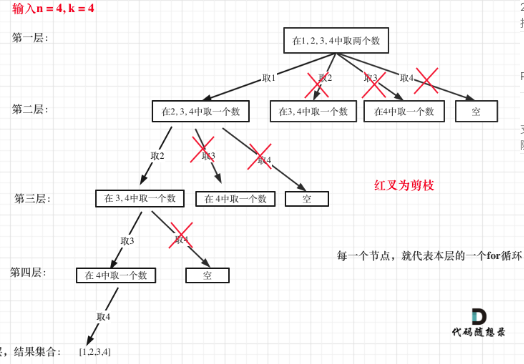
func combine(n int, k int) [][]int {res := [][]int{}path := []int{}var travel func(n int,k int,start int)travel = func(n int,k int ,start int){if len(path) == k{tempCopy := make([]int,k)copy(tempCopy,path)res = append(res,tempCopy)return }for i := start;i <= n;i++{if n - start + 1 < k -len(path) {break}path = append(path,i)travel(n,k,i+1)path = path[:len(path)-1]}}travel(n,k,1)return res
}
2.216. 组合总和 III - 力扣(LeetCode)
func combinationSum3(k int, n int) [][]int {res := [][]int{}path := []int{}var dfs func(k int,n int,start int)dfs = func(k int ,n int,start int){if n == 0 && len(path) == k{copyTemp := make([]int,len(path))copy(copyTemp,path)res = append(res,copyTemp)return}if len(path) == k && n != 0{return}for i := start;i<=9;i++{if i > n{return}path = append(path,i)dfs(k,n-i,i+1)path = path[:len(path)-1]}}dfs(k,n,1)return res
}感悟:很熟练,做回溯问题的时候,脑袋里需要构建那个树的图,这样代码也好写
3.17. 电话号码的字母组合 - 力扣(LeetCode)
func letterCombinations(digits string) []string {m := []string{"abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"}path := []byte{}res := []string{}if digits == ""{return res}var dfs func(start int)dfs = func(start int){if len(path) == len(digits){tmp := string(path)res = append(res,tmp)return }//digit := strconv.Atoi(digits[start])//转换成intdigit := int(digits[start] - '0')str := m[digit-2]for j := 0;j < len(str);j++{path = append(path,str[j])if start + 1 > len(digits){return }dfs(start+1)path = path[:len(path)-1]}
}dfs(0)return res
}
感悟:题不难,就是字符串和字符串转换略繁琐
比如//digit := strconv.Atoi(digits[start])//转换成int,传的参数只能是string类型的,但对于byte,用最基本的int(digits[start] - '0'就可以了
4.39. 组合总和 - 力扣(LeetCode)
无重复数组,能被反复选取
func combinationSum(candidates []int, target int) [][]int {res := [][]int{}path := []int{}sort.Ints(candidates)//升序var dfs func(start int,target int)dfs = func(start int,target int){if target == 0{tmp := make([]int,len(path))copy(tmp,path)res = append(res,tmp)return}for i := start;i<len(candidates);i++{if candidates[i]>target{break}path = append(path,candidates[i])dfs(i,target - candidates[i])path = path[:len(path)-1]}}dfs(0,target)return res
}感悟:对于dfs(candidates,i,target - candidates[i]),题目允许 同一个元素被多次选取,所以使用了 i作为下一轮递归的起始索引。
5.40. 组合总和 II - 力扣(LeetCode)
有重复数组,不能被反复选取
func combinationSum2(candidates []int, target int) [][]int {res := [][]int{}path := []int{}sort.Ints(candidates)//升序var dfs func(start int,target int)dfs = func(start int,target int){if target == 0{tmp := make([]int,len(path))copy(tmp,path)res = append(res,tmp)return}for i := start;i<len(candidates);i++{if candidates[i]>target{break}if i>start && candidates[i] == candidates[i-1]{continue}path = append(path,candidates[i])dfs(i+1,target - candidates[i])path = path[:len(path)-1]}}dfs(0,target)return res
}
感悟:对于dfs(candidates,i+1,target - candidates[i]),题目不允许 同一个元素被多次选取,所以使用了 i+1作为下一轮递归的起始索引。
对于 if i>start && candidates[i] == candidates[i-1]{continue},这里第一次写成i>1了,i>start 的含义是:只跳过 “当前递归层级中” 的重复元素,而不是跳过所有位置的重复元素。若用 i>1,会错误地跳过非同一层级的合法元素(比如 candidates = [1,1,2] 中,第一个层级的 i=0 是第一个 1,第二个层级的 i=1 是第二个 1,此时 i>start(start=1,i=1 不满足 i>start),允许选择第二个 1,但 i>1 会直接跳过,导致合法组合丢失)。所以start代表层级的开始
切割问题
对比下面两个算法,仔细想想,其实就是多了str := s[start:i+1],也就是在for循环中进行分割,然后
6.131. 分割回文串 - 力扣(LeetCode)
func partition(s string) [][]string {res := [][]string{}path := []string{}var dfs func(s string,start int)//遍历切割点
dfs = func(s string ,start int){if start == len(s){tmp := make([]string, len(path))copy(tmp, path)res = append(res, tmp)return }for i := start;i<len(s);i++{str := s[start:i+1]if isPalindrome(str){path = append(path,str)dfs(s,i+1)path = path[:len(path)-1]}}
}dfs(s,0)return res
}func isPalindrome(s string)bool{for i,j := 0,len(s)-1;i < j;i,j = i+1,j-1{
//go语法,不能写成i++,j--。因为逗号不能分割语句if s[i] != s[j]{return false}}return true
}感悟:本道题最开始的纠结点是:为什么要遍历到找到回文串,然后再往下遍历。
顺便复习一下动态规划版的判断序列回文:【注意到序计算】
func computePalindrome(s string) {// isPalindrome[i][j] 代表 s[i:j](双边包括)是否是回文字串 isPalindrome = make([][]bool, len(s))for i := 0; i < len(isPalindrome); i++ {isPalindrome[i] = make([]bool, len(s))}for i := len(s)-1; i >= 0; i-- {// 需要倒序计算, 保证在i行时, i+1行已经计算好了for j := i; j < len(s); j++ {if j == i {isPalindrome[i][j] = true} else if j - i == 1 {isPalindrome[i][j] = s[i] == s[j]} else {isPalindrome[i][j] = s[i] == s[j] && isPalindrome[i+1][j-1]}}}
}7.93. 复原 IP 地址 - 力扣(LeetCode)
func restoreIpAddresses(s string) []string {path := []string{}res := []string{}var dfs func(s string,start int)dfs = func(s string,start int){if len(path)==4{if start == len(s){str := strings.Join(path,".")res = append(res,str)}return}for i := start;i<len(s);i++{if i != start &&s[start]=='0'{//含有前导0break}str := s[start:i+1]num , _ := strconv.Atoi(str)if num >= 0 && num <= 255{path = append(path,str)dfs(s,i+1)path = path[:len(path)-1]}else{break}}}dfs(s,0)return res
}感悟:本题要三刷,还是不太熟练。其实本题和上体一样都是用start去找切割点。同时strings.Join(path,".")第一次用
减枝之后:
func restoreIpAddresses(s string) []string {path := []string{}res := []string{}if len(s) < 4 || len(s) >12{//合理的IPreturn res} var dfs func(start int)dfs = func(start int){if len(path) == 4{if start == len(s){//分割点是否遍历完str := strings.Join(path,".")res = append(res,str)}return}for _, c := range s {if c < '0' || c > '9' {return res // 存在非数字字符,直接返回空结果}}need := 4 - len(path) //还需到的段remain := len(s) - start//剩余字符数if remain < need || remain >3*need{return}end := start + 3if end > len(s){end = len(s)}for i := start;i<end;i++{if s[start] == '0' && i != start{//前导零问题的规避break}num,_ := strconv.Atoi(s[start:i+1])if num >=0 && num <=255 && err == nil{path = append(path,s[start:i+1])dfs(i+1)path = path[:len(path)-1]}else{break}}}dfs(0)return res
}子集问题
感悟:子集问题和上述不同,上述是求叶子结点,子集问题相当于求所有的节点
8.78. 子集 - 力扣(LeetCode)
不重复元素,不重复子集
func subsets(nums []int) [][]int {path := []int{}res := [][]int{}var dfs func(start int)dfs = func(start int){tmp := make([]int,len(path))copy(tmp,path)res = append(res,tmp)for i := start;i<len(nums);i++{path = append(path,nums[i])dfs(i+1)path = path[:len(path)-1]}}dfs(0)return res
}
9.90. 子集 II - 力扣(LeetCode)
重复元素,不重复子集
方一:不使用used数组
func subsetsWithDup(nums []int) [][]int {res := [][]int{}path := []int{}sort.Ints(nums)var dfs func(start int)dfs = func(start int){tmp := make([]int,len(path))copy(tmp,path)res = append(res,tmp)for i := start;i<len(nums);i++{if i != start && nums[i] == nums[i-1]{continue}path = append(path,nums[i])dfs(i+1)path = path[:len(path)-1]}}dfs(0)return res
}方二:使用used数组
每个递归层级都有一个独立的 used 字典。同一树层不重复选相同元素,但同一树枝可以重复选。标记 “元素是否在当前树枝中被使用过”,需跨递归层级传递状态
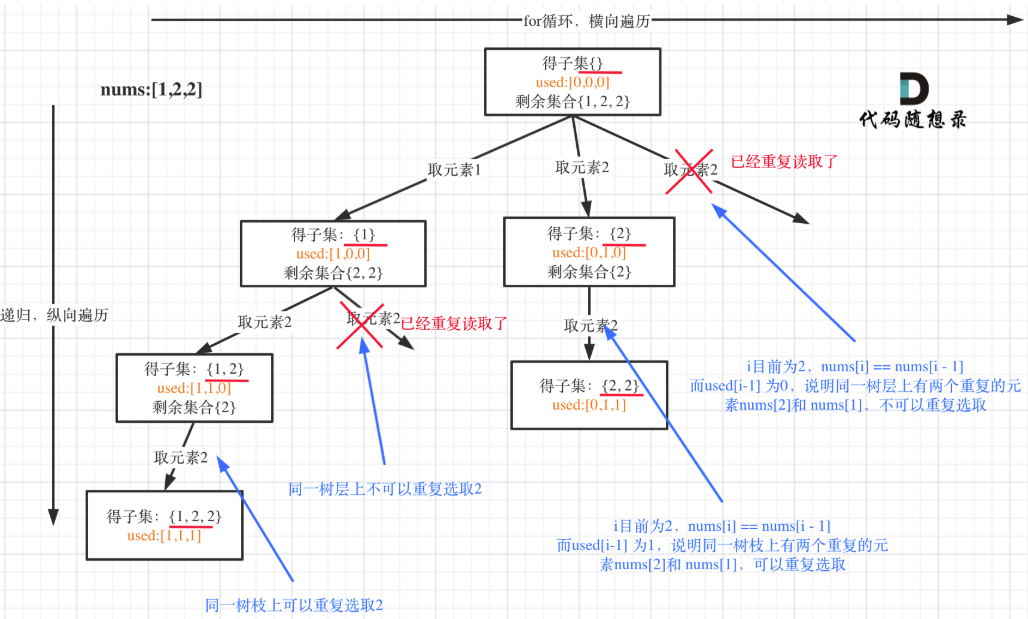
func subsetsWithDup(nums []int) [][]int {result := make([][]int, 0)path := make([]int, 0)used := make([]bool, len(nums))sort.Ints(nums) // 排序为去重做准备var backtracing func(startIndex int)backtracing = func(startIndex int) {tmp := make([]int, len(path))copy(tmp, path)result = append(result, tmp)for i := startIndex; i < len(nums); i++ {// 去重逻辑:同一树层的重复元素跳过if i > 0 && nums[i] == nums[i-1] && !used[i-1] {continue}path = append(path, nums[i])used[i] = truebacktracing(i + 1) // 递归path = path[:len(path)-1] // 回溯路径used[i] = false // 回溯使用状态}}backtracing(0)return result
}// used[i - 1] == true,说明同一树枝candidates[i - 1]使用过// used[i - 1] == false,说明同一树层candidates[i - 1]使用过使用层级used
func subsetsWithDup(nums []int) [][]int {result := make([][]int, 0)path := make([]int, 0)sort.Ints(nums) // 排序为去重做准备var backtracing func(startIndex int)backtracing = func(startIndex int) {tmp := make([]int, len(path))copy(tmp, path)result = append(result, tmp)levelused := make(map[int]bool)for i := startIndex; i < len(nums); i++ {// 去重逻辑:同一树层的重复元素跳过if levelused[nums[i]] == true{continue}path = append(path, nums[i])levelused[nums[i]] = truebacktracing(i + 1) // 递归path = path[:len(path)-1] // 回溯路径}}backtracing(0)return result
}10.491. 非递减子序列 - 力扣(LeetCode)
同一树层不重复选相同元素,不可以打乱顺序,仅标记 “当前树层是否已使用过该值”,无需跨层级传递
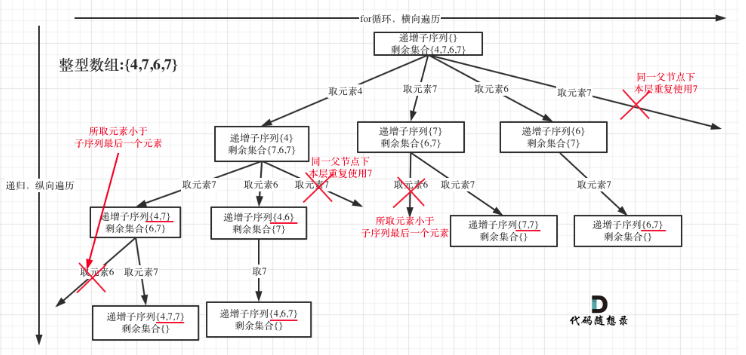
func findSubsequences(nums []int) [][]int {path := []int{}res := [][]int{}var dfs func(start int)dfs = func(start int){if len(path)>1{temp := make([]int,len(path))copy(temp,path)res = append(res,temp)}used := make(map[int]bool)for i := start;i<len(nums);i++{if used[nums[i]]{continue}if len(path) == 0 || nums[i] >= path[len(path)-1]{path = append(path,nums[i])used[nums[i]] = truedfs(i+1)path = path[:len(path)-1]}}}dfs(0)return res
}感悟:对于used数组,最开始写的代码没有考虑[4,7,6,7]这种情况,只考虑了if i != start && nums[i] == nums[i-1]{ continue }
排列问题
11.46. 全排列 - 力扣(LeetCode)
不重复数字
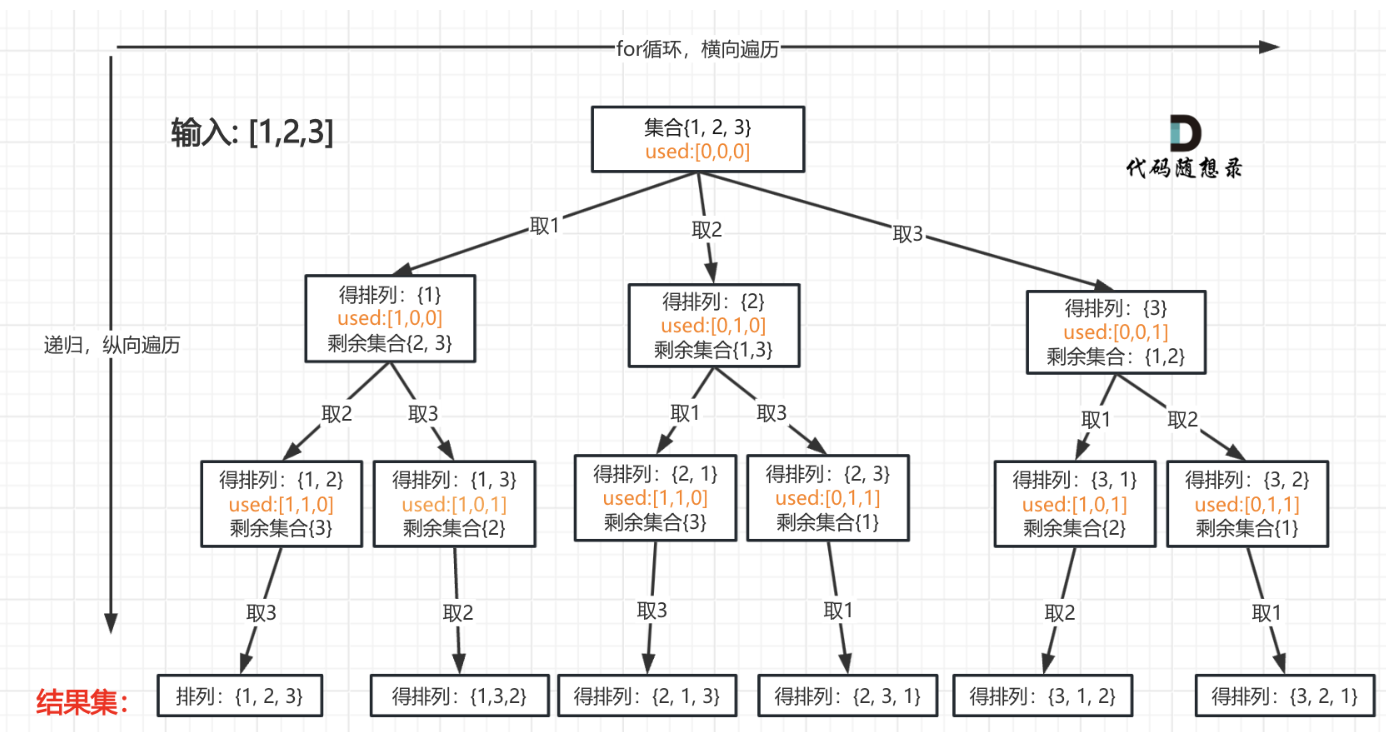
func permute(nums []int) [][]int {res := [][]int{}path := []int{}used := make([]bool,len(nums))var dfs func()dfs = func(){if len(path) == len(nums){temp := make([]int,len(path))copy(temp,path)res = append(res,temp)}for i := 0;i<len(nums);i++{if used[i] == false{path = append(path,nums[i])used[i] = truedfs()used[i] = falsepath = path[:len(path)-1]}}}dfs()return res
}感悟:这道题很基础,利用used数组去重,比如[1,2,3],第二次选择2的时候,在第二层就不会重复选择2了,因为已经选择过了
12.47. 全排列 II - 力扣(L eetCode)
重复数字
1a 1b 2
1a 1b 2
1a 1b
删除1b可以是levelused,也可以是i != 0 && nums[i] == nums[i-1] && used[i-1] == false
删除第二层的1a,就要用used[i] == true(代表上一层存过了)
//不使用哈希表
func permuteUnique(nums []int) [][]int {res := [][]int{}path := []int{}used := make([]bool,len(nums))sort.Ints(nums)//让相同元素相邻,便于去重var dfs func()dfs = func(){if len(path) == len(nums){temp := make([]int,len(path))copy(temp,path)res = append(res,temp)}for i := 0;i < len(nums);i++{if i != 0 && nums[i] == nums[i-1] && used[i-1] == false{continue}//同一层级的元素重复if used[i] == false{//同一树枝看这个元素有没有被使用过,比如[1,1,2]会出现[1,1,1]path = append(path,nums[i])used[i] = truedfs()used[i] = falsepath = path[:len(path)-1]}}}dfs()return res
}
//使用哈希表
func permuteUnique(nums []int) [][]int {res := [][]int{}path := []int{}used := make([]bool,len(nums))sort.Ints(nums)//让相同元素相邻,便于去重var dfs func()dfs = func(){if len(path) == len(nums){temp := make([]int,len(path))copy(temp,path)res = append(res,temp)}levelused := make(map[int]bool)for i := 0;i < len(nums);i++{if used[i] || levelused[nums[i]]{continue//如果元素已被选入路径或者当前层级已经选过}used[i] = truelevelused[nums[i]] = truepath = append(path,nums[i])dfs()used[i] = falsepath = path[:len(path)-1]}}dfs()return res
}感悟:对于used数组和层级used数组逐渐有了更深的了解。对于levelused控制了同一层级去重的逻辑,同时对于[1,1,2]肯能会出现[1,1,1]的情况,还要引入一个全局变量(跨层级的)used,即控制单个排列中元素不重复出现的逻辑。所以还要用used[i]==true去判断。
重新安排行程
图论深搜+回溯
13.332. 重新安排行程 - 力扣(LeetCode)
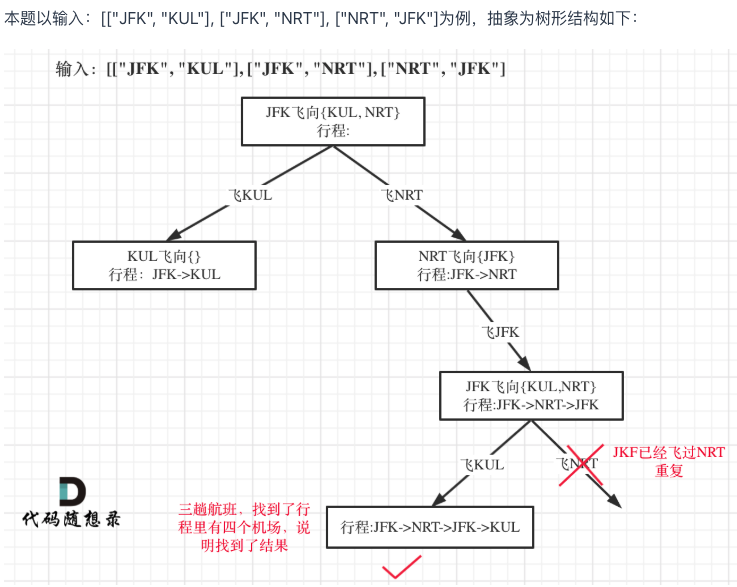
func findItinerary(tickets [][]string) []string {// 1. 构建出发机场到目的地列表的映射(值为字符串切片,便于排序和删除)targets := make(map[string][]string)for _, ticket := range tickets {from, to := ticket[0], ticket[1]targets[from] = append(targets[from], to)}// 2. 对每个出发机场的目的地列表按字典序排序(核心:保证贪心选择的正确性)for from := range targets {sort.Strings(targets[from])}result := []string{}// 3. 深度优先搜索(DFS):优先选择字典序最小的目的地,使用后删除var dfs func(from string)dfs = func(from string) {// 遍历当前机场的所有目的地(排序后,按顺序取第一个)for len(targets[from]) > 0 {// 取第一个目的地(字典序最小)to := targets[from][0]// 删除该目的地(标记为已使用,避免重复遍历)targets[from] = targets[from][1:]// 递归前往下一个机场dfs(to)}// 4. 后序遍历:当当前机场无可用目的地时,加入结果(最终反转得到正确顺序)result = append(result, from)}// 从 JFK 出发开始DFSdfs("JFK")// 反转结果:后序遍历的顺序是“终点→起点”,反转后变为“起点→终点”reverse(result)return result
}// 辅助函数:反转切片
func reverse(s []string) {for i, j := 0, len(s)-1; i < j; i, j = i+1, j-1 {s[i], s[j] = s[j], s[i]}
}感悟:困难题好难,需要二刷以上,并且本题特别巧妙。其中刚才的纠结点:对于成环情况的处理。题目保证了输入一定存在这样的通路,因此算法不需要专门 “规避” 环,而是通过贪心策略和后序遍历,自然处理环的情况。
棋盘问题
14.51. N 皇后 - 力扣(LeetCode)
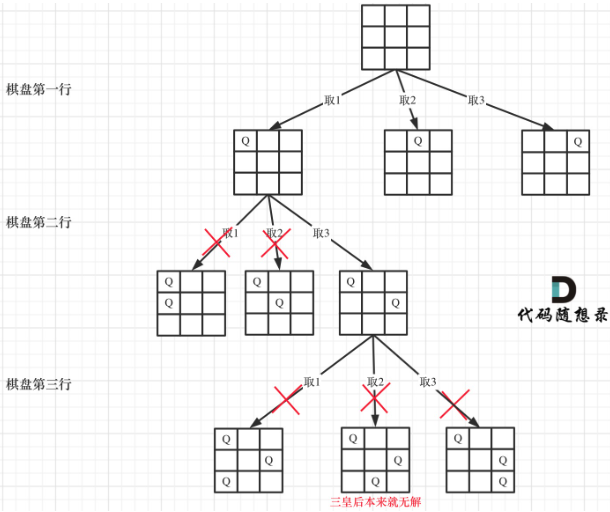
func solveNQueens(n int) [][]string {res := [][]string{}chessboard := make([][]string,n)for i := 0;i<n;i++{//初始化棋盘chessboard[i] = make([]string,n) }for i := 0;i<n;i++{for j:= 0;j<n;j++{chessboard[i][j] = "."}}var backtrack func(int)backtrack = func(row int){if row == n{temp := make([]string,n)for i,str := range chessboard{temp[i] = strings.Join(str,"")}res = append(res,temp)return}for i := 0;i<n;i++{if isValid(n,row,i,chessboard){chessboard[row][i] = "Q"backtrack(row+1)chessboard[row][i] = "."}}}backtrack(0)return res
}func isValid(n,row,col int,chessboard [][]string)bool{for i := 0;i<row;i++{//竖着的有没有if chessboard[i][col] == "Q"{return false}}for i,j := row-1,col+1;i>=0&&j<n;i,j = i-1,j+1{//对角线if chessboard[i][j] == "Q"{return false}} for i,j:= row-1,col-1;i>=0&&j>=0;i,j = i-1,j-1{//对角线if chessboard[i][j] == "Q"{return false}} return true
}感悟:本题其实还好,就是通过回溯法去选择对应的位置,然后分别用isValid去判断该位置是否可行。棋盘问题相当于一维转换成了二维。
15.37. 解数独 - 力扣(LeetCode)
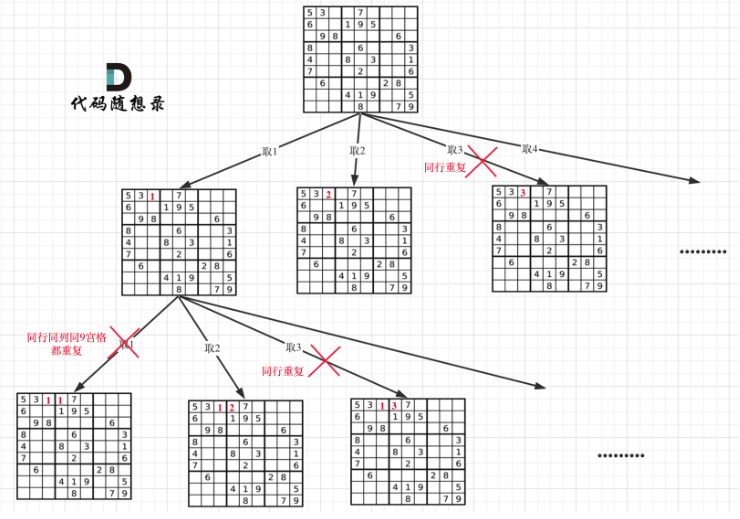
func solveSudoku(board [][]byte) {n := len(board)var backtracking func()boolbacktracking = func()bool{for i := 0;i<n;i++{for j:= 0;j<n;j++{if board[i][j] != '.'{continue}for k := '1';k<='9';k++{if isValid(i,j,byte(k),board) == false{continue}else{//满足board[i][j] = byte(k)if backtracking() == true{return true}board[i][j] = '.'}}return false}}return true}backtracking()
}func isValid(row,col int,k byte,board[][]byte)bool{//行for i := 0;i < 9;i++{if board[row][i] == k{return false}}//列for i := 0;i < 9;i++{if board[i][col] == k{return false}}//方格startrow := (row / 3) * 3startcol := (col / 3) * 3for i:= startrow;i<startrow+3;i++{for j:= startcol;j<startcol+3;j++{if board[i][j] == k{return false}}}return true
}感悟:本题解法和N皇后差不多,主要就是写isValid函数,然后以二维的形式去。然后递归回溯,就是两个循环遍历看那个元素合不合法。做完之后不是很难呢。
