HDU7321-KongMingQi孔明棋(找规律）

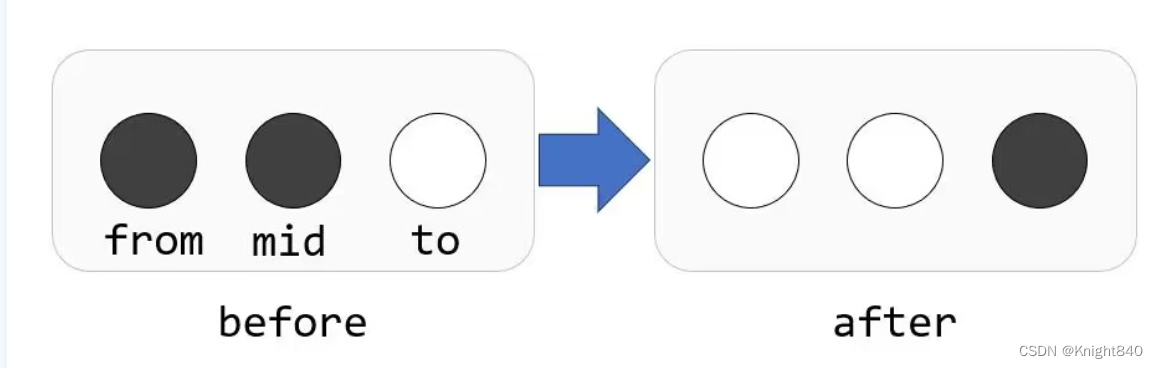
题意：给你规定初始状态有个棋子，放到的矩阵棋盘上，除了四条外边，其余各放一枚棋子。孔明棋在棋盘内移动一颗棋子的必要条件是：棋子的起点和终点之间有且仅有一个格子，并且格子上必须有一颗棋子，终点没有棋子，图示如下。问最后最少能剩多少棋子。

思路：先看懂下图的转换过程：

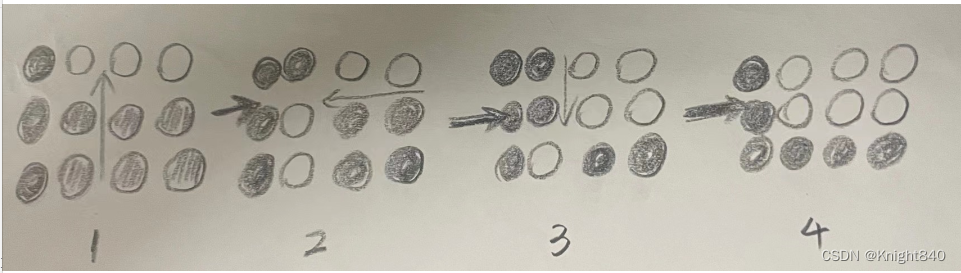
可以发现图4比图1少了个1x3的小矩阵，可以用上述操作在这三列上消去很多1x3矩阵。若操作到这三列只剩一个2x3的小矩阵，可以从上述图3转到下面操作，将两排同时消去：

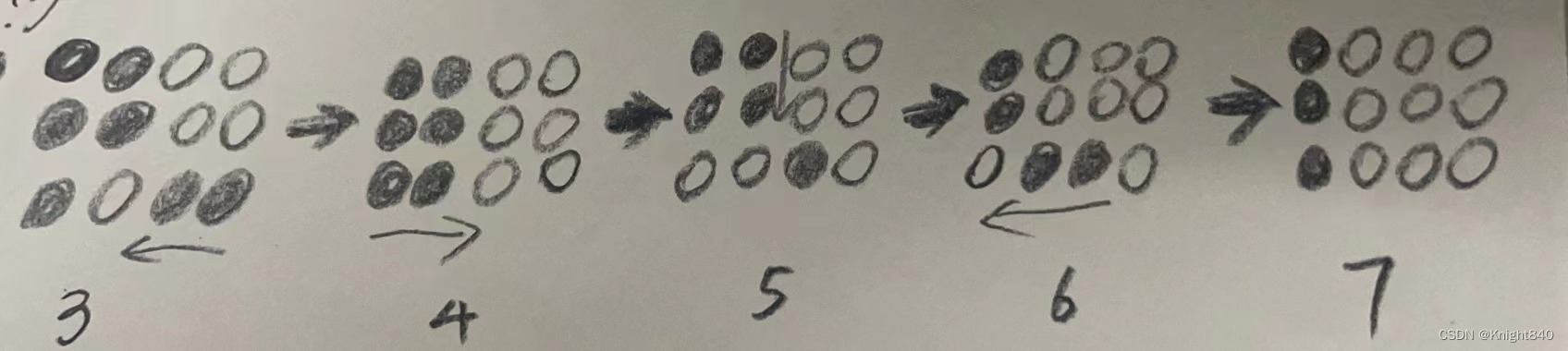
可以看出这两种操作的条件都是要行数大于1并且由于第二种操作需要借助最左边一列辅助，所以列数要大于等于4。所以我们可以得出个小结论：若矩阵行数大于1、列数大于等于4，就可以消去三列，也就是if(n>1&&m>=4): 。重复这个操作就可以将矩阵列数变到4以内。由于此题行列等价,所以重复此操作可以将n和m都缩小到小于4的范围。n或者m等于1的情况可以直接计算。其余只剩2*2，2*3，3*3的情况，可以手动模拟得出结果。

#include<bits/stdc++.h>
using namespace std;int main()
{int T;cin >> T;while (T--){int n, m;cin >> n >> m;//1特判就行了 if (n == 1){cout << (m + 1) / 2 << endl;continue;}if (m == 1){cout << (n + 1) / 2 << endl;continue;}while (n >= 4){n -= 3;}while (m >= 4){m -= 3;}//减完若又出现1 if (n == 1){cout << (m + 1) / 2 << endl;continue;}if (m == 1){cout << (n + 1) / 2 << endl;continue;}//3种情况直接得出答案 if (n + m == 4)//2*2{cout << 1 << endl;}else if(n+m==5)//2*3或者3*2 {cout << 2 << endl;}else if (n + m == 6)//3*3{cout << 2 << endl;}}return 0;
}