当前位置：首页 > ds >正文

Python基于PCA、PCA-kernel、LDA的同心圆数据降维项目实战

ds 2025/8/18 14:31:51

说明：这是一个机器学习实战项目（附带数据+代码+文档），如需数据+代码+文档可以直接到文章最后关注获取。

1.项目背景

在数据分析与机器学习领域，降维技术是处理高维数据集的关键步骤之一，它有助于简化模型、减少计算成本并提升算法性能。特别地，当面对复杂的数据结构时，如同心圆数据集，如何有效提取关键特征成为了一个挑战。本项目旨在探索和比较三种不同的降维方法：主成分分析（PCA）、核主成分分析（Kernel PCA）以及线性判别分析（LDA）。通过应用这些方法对合成的同心圆数据进行降维处理，我们期望能够揭示不同方法在处理非线性分布数据上的优势与局限性。此外，本研究还将探讨如何利用降维结果来提高后续分类任务的准确性。

选择同心圆数据集作为研究对象的原因在于其独特的几何特性，该数据集由两组或多组圆形区域组成，每组代表一个类别，但它们之间存在复杂的非线性边界。这种结构使得传统的线性降维方法（如PCA）难以有效地分离不同类别的数据点。因此，本项目不仅关注于PCA等线性方法的表现，还将深入评估Kernel PCA和LDA这两种能够捕捉数据中潜在非线性关系的技术。通过对这三种方法进行全面对比分析，我们可以为实际应用中的数据预处理阶段提供有力指导，尤其是在需要处理具有复杂内在结构的数据集时。最终目标是为相关领域的研究人员和从业者提供有价值的参考依据。

本项目通过Python基于PCA、PCA-kernel、LDA的同心圆数据降维项目实战。

2.数据获取

本次建模数据来源于网络(本项目撰写人整理而成)，数据项统计如下：

编号	变量名称	描述
1	Feature_1	数据点的横坐标（第一维特征）
2	Feature_2	数据点的纵坐标（第二维特征）
3	Label	类别标签，0 表示外圆，1 表示内圆

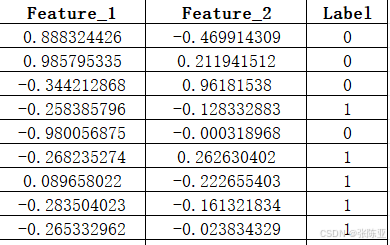
数据详情如下(部分展示)：

3.数据预处理

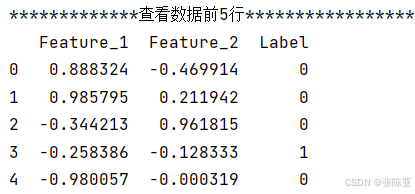
3.1 用Pandas工具查看数据

使用Pandas工具的head()方法查看前五行数据：

关键代码：

3.2数据缺失查看

使用Pandas工具的info()方法查看数据信息：

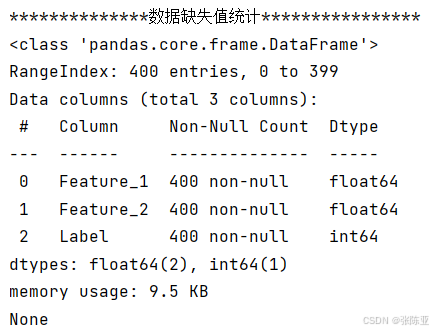
从上图可以看到，总共有3个变量，数据中无缺失值，共400条数据。

关键代码：

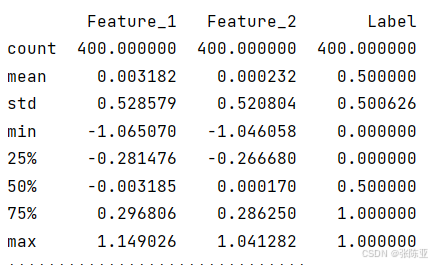
3.3数据描述性统计

通过Pandas工具的describe()方法来查看数据的平均值、标准差、最小值、分位数、最大值。

关键代码如下：

4.探索性数据分析

4.1 柱状图

用Matplotlib工具的plot()方法绘制柱状图：

4.2 分布直方图

用Matplotlib工具的hist()方法绘制直方图：

4.3 相关性分析

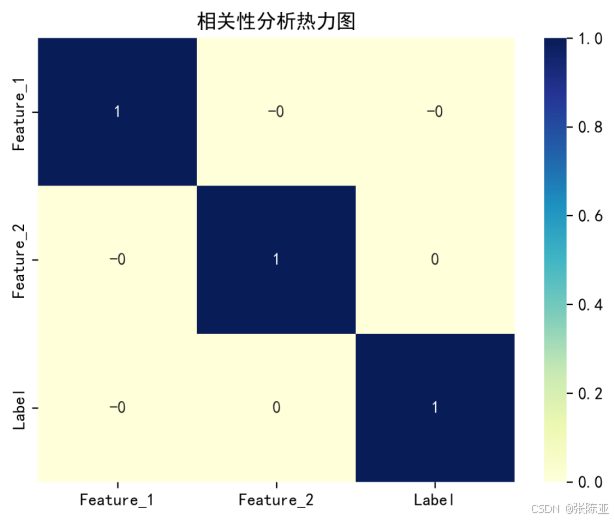
从上图中可以看到，数值越大相关性越强，正值是正相关、负值是负相关。

5.特征工程

5.1 建立特征数据和标签数据

关键代码如下：

6.构建降维模型

主要通过Python基于PCA、PCA-kernel、LDA的同心圆数据降维算法，用于目标降维。

6.1 构建模型

模型名称	模型参数
PCA模型	n_components=1
PCA-kernel模型	n_components=1
PCA-kernel模型	kernel='rbf'
LDA模型	n_components=1

7.模型评估

7.1降维结果可视化

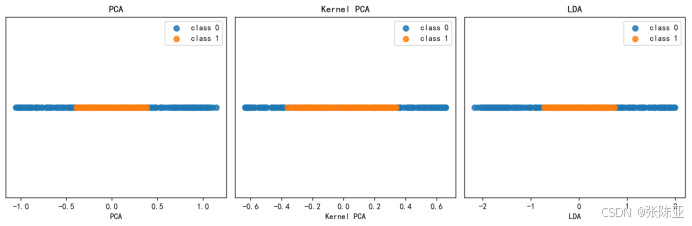
通过对PCA、Kernel PCA和LDA三种降维方法在同心圆数据集上的应用结果进行对比分析，我们可以清晰地看到它们各自的特点和适用场景。PCA作为一种线性降维方法，在处理非线性结构的数据时表现有限，如图所示，两类数据在PCA后的投影上仍然存在重叠，未能有效分离。相比之下，Kernel PCA通过引入核函数，能够捕捉到数据中的非线性关系，使得原本难以区分的两类数据在投影后呈现出较为明显的分界，但仍有少量重叠。而LDA作为监督学习方法，利用类别信息进行降维，其效果最为显著，两类数据在LDA投影下几乎完全分离，显示出强大的分类能力。这表明在处理具有复杂结构的数据时，选择合适的降维方法至关重要，Kernel PCA和LDA更适合处理非线性问题，而PCA则适用于线性可分的情况。因此，在实际应用中，应根据数据特性和任务需求灵活选择降维方法，以达到最佳效果。