机器学习西瓜书

机器学习基础

模型评估、选择与验证

欠拟合和过拟合

欠拟合：模型在训练集上误差很高；
欠拟合的原因：模型过于简单，没有很好的捕捉到数据特征，不能很好的拟合数据。

过拟合：在训练集上误差低，测试集上误差高；
过拟合原因：模型把数据学习的太彻底，以至于把噪声数据的特征也学习到了，这样就会导致在后期测试的时候不能够很好地识别数据，模型泛化能力太差。

过拟合的解决方案：

模型复杂度相关

• 简化模型：
  减少模型参数（比如减少神经网络层数、每层神经元数）来降低模型的复杂度。

• 正则化（Regularization）：

  • L1正则化（Lasso）：鼓励稀疏解（部分权重为0）

  • L2正则化（Ridge）：惩罚大权重，平滑模型

• 剪枝（用于决策树）：
  限制树的深度、叶节点最小样本数等，减少过拟合风险。

• 交叉验证（Cross-Validation）：
  用于选择合适的模型参数和防止在验证集上过拟合。

• 提早停止（Early Stopping）：
  在验证集误差开始上升时停止训练，避免模型继续记忆训练集。

• Dropout（用于神经网络）：
  训练时随机丢弃部分神经元，防止特征依赖过强。

数据相关

• 增加训练数据：
  更多样本有助于模型学习更真实的数据分布，减小泛化误差。

• 数据增强（Data Augmentation）：
  常用于图像、文本领域。例如旋转、翻转图像，或打乱句子结构。

偏差与方差

模型误差来源

模型在训练集上的误差主要来自于偏差，在测试集上的误差主要来源于方差。

上图表示，如果一个模型在训练集上正确率为 80%，测试集上正确率为 79% ，则模型欠拟合，其中 20% 的误差来自于偏差，1% 的误差来自于方差。如果一个模型在训练集上正确率为 99%，测试集上正确率为 80% ，则模型过拟合，其中 1% 的误差来自于偏差，19% 的误差来自于方差。

可以看出，欠拟合是一种高偏差的情况。过拟合是一种低偏差，高方差的情况。

偏差与方差

偏差：预计值的期望与真实值之间的差距

方差：预测值的离散程度，也就是离其期望值的距离

以射击打靶为例，蓝色的小点是我们在靶子上的射击记录，蓝色点的质心（黑色点）到靶心的距离为偏差，某个点到质心的距离为方差。所以，某个点到质心的误差就是由偏差与方差所组成。那么，为什么欠拟合是一直高偏差情况，过拟合是一种低偏差高方差情况呢？

欠拟合是因为模型过于简单，模型过于简单我们可以当做是我们射击时射击的范围比较小，它所涵盖的范围不包括靶心，所以无论怎么射击，射击点的质心里靶心的距离都很远，所以偏差很高。但是因为射击范围很小，所以所有射击点相互离的比较紧密，则方差低。

过拟合是模型过于复杂，可以理解为这个时候射击范围很大，经过不断的训练射击的点的质心离靶心的距离很近了，但是数据量有限，而射击范围大，所以所有射击点之间很离散，方差大。

如果一个模型，它在训练集上正确率为85%，测试集上正确率为80%，则模型是过拟合还是欠拟合?其中，来自于偏差的误差为?来自方差的误差为?
A、欠拟合，5%，5%
B、欠拟合，15%，5%
C、过拟合，15%，15%
D、过拟合，5%，5%

误差总 = 偏差 + 方差 + 不可约误差

选B

验证集和交叉验证

为什么需要验证集

从严格意义上来讲，测试集只能在所有超参数和模型参数选定后使用一次，不可以使用测试数据选择模型。由于无法从训练误差估计泛化误差，因此也不应只依赖训练数据选择模型。鉴于此，我们可以预留⼀部分在训练数据集和测试数据集以外的数据来进⾏模型选择。这部分数据被称为验证数据集，简称验证集。

k折交叉验证

由于验证数据集不参与模型训练，当训练数据不够用的时候，预留大量的验证数据太奢侈，使用k折交叉验证改善。

k折交叉验证中，将原始的训练集分成k个不重合的子数据，然后我们做K次模型训练和验证。每⼀次，我们使⽤⼀个⼦数据集验证模型，并使⽤其它 K−1 个⼦数据集来训练模型。在这 K 次训练和验证中，每次⽤来验证模型的⼦数据集都不同。最后，我们对这 K 次训练误差和验证误差分别求平均。

看图就能很容易看懂，下图是五折交叉验证

集成学习

在机器学习的有监督学习算法中，我们的目标是学习出一个稳定的且在各个方面表现都较好的模型，但实际情况往往不这么理想，有时我们只能得到多个有偏好的模型（弱监督模型，在某些方面表现的比较好）。集成学习就是组合这里的多个弱监督模型以期得到一个更好更全面的强监督模型。

集成学习的思想是：即使某一个弱分类器得到了错误的预测，其他的弱分类器也可以将错误纠正回来。集成方法是将几种机器学习技术组合成一个预测模型的元算法，以达到减小方差、偏差或改进预测的效果。

自助法

在统计学中，自助法是一种从给定训练集中有放回的均匀抽样，也就是说，每当选中一个样本，它等可能地被再次选中并被再次添加到训练集中。

自助法以自助采样法为基础，给定包含 m 个样本的数据集 D，我们对它进行采样产生数据集 D'；每次随机从 D 中挑选一个赝本，将其拷贝放入 D'，然后再将该样本放回初始数据集 D 中，使得该样本在下次采样时仍有可能被采到；这个过程重复执行 m 次后，就得到了包含m个样本的数据集 D'，这就是自助采样的结果。

自助法在数据集较小、难以有效划分训练/测试集时很有用；此外，自助法能从初始数据集中产生多个不同的训练集，这对集成学习等方法有很大的好处。然而，自助法产生的数据集改变了初始数据集的分布，这会引入估计偏差。

1、假设，我们现在利用5折交叉验证的方法来确定模型的超参数，一共有4组超参数，我们可以知道，5折交叉验证，每一组超参数将会得到5个子模型的性能评分，假设评分如下，我们应该选择哪组超参数？
A、子模型1:0.8 子模型2:0.7 子模型3:0.8 子模型4:0.6 子模型5:0.5
B、子模型1:0.9 子模型2:0.7 子模型3:0.8 子模型4:0.6 子模型5:0.5
C、子模型1:0.5 子模型2:0.6 子模型3:0.7 子模型4:0.6 子模型5:0.5
D、子模型1:0.8 子模型2:0.8 子模型3:0.8 子模型4:0.8 子模型5:0.6

答案：D

2.（多选）下列说法正确的是？
A、相比自助法，在初始数据量较小时交叉验证更常用。
B、自助法对集成学习方法有很大的好处
C、使用交叉验证能够增加模型泛化能力
D、在数据难以划分训练集测试集时，可以使用自助法

答案：BCD

衡量回归的性能指标

MSE 均方误差

RMSE

要做房价预测，每平方是万元，预测结果也是万元，那么差值的平方单位应该是千万级别的。开个根号就好了。我们误差的结果就跟我们数据是一个级别的了，在描述模型的时候就说，我们模型的误差是多少万元。

MAE

R-Squared

1.R方越接近于1越好

2.当我们的模型和基模型性能相同时，取0

3.如果为负数，则说明我们训练出来的模型还不如基准模型，此时，很有可能我们的数据不存在任何线性关系。

1、下列说法正确的是？
A、相比MSE指标，MAE对噪声数据不敏感
B、RMSE指标值越小越好
C、R-Squared指标值越小越好
D、当我们的模型不犯任何错时，R-Squared值为0

答案：AB

准确度的陷阱与混淆矩阵

混淆矩阵

想进一步的考量分类模型的性能如何，可以使用其他的一些性能指标，例如精准率和召回率。但这些指标计算的基础是混淆矩阵。

继续以癌症检测系统为例，癌症检测系统的输出不是有癌症就是健康，这里为了方便，就用 1 表示患有癌症，0 表示健康。假设现在拿 10000 条数据来进行测试，其中有 9978 条数据的真实类别是 0，系统预测的类别也是 0，有 2 条数据的真实类别是 1 却预测成了 0，有 12 条数据的真实类别是 0 但预测成了 1，有 8 条数据的真实类别是 1，预测结果也是 1。

如果我们把这些结果组成如下矩阵，则该矩阵就成为混淆矩阵。

用代码写混淆矩阵

import numpy as npdef confusion_matrix(y_true, y_predict):'''构建二分类的混淆矩阵，并将其返回:param y_true: 真实类别，类型为ndarray:param y_predict: 预测类别，类型为ndarray:return: shape为(2, 2)的ndarray'''#********* Begin *********#def TN(y_true, y_predict):"""代表真实类别是Negative，预测结果也是Negative的数量"""return np.sum((y_true==0)&(y_predict==0))def TP(y_true, y_predict):"""代表真实类别是Positive，预测结果也是Positive的数量"""return np.sum((y_true==1)&(y_predict==1))def FN(y_true,y_predict):"""F代表预测错了，N表示预测结果是Negative"""return np.sum((y_true==1)&(y_predict==0))def FP(y_true,y_predict):"""F代表预测错了，N表示预测结果是Positive"""return np.sum((y_true==0)&(y_predict==1))return np.array([[TN(y_true, y_predict), FP(y_true, y_predict)],[FN(y_true, y_predict), TP(y_true, y_predict)]])#********* End *********#

精准率与召回率

精确率

精确率是指预测模型为Positive时的预测准确度。

召回率

我们关注的事件发生了，并且模型预测正确了的比值。感觉这个得记忆例子，假设有100个患有癌症的病人使用这个系统检测癌症，系统能检测出80人是患有癌症的。

import numpy as npdef precision_score(y_true, y_predict):'''计算精准率并返回:param y_true: 真实类别，类型为ndarray:param y_predict: 预测类别，类型为ndarray:return: 精准率，类型为float'''#********* Begin *********#def TP(y_true, y_predict):"""代表真实类别是Positive，预测结果也是Positive的数量"""return np.sum((y_true==1)&(y_predict==1))def FP(y_true,y_predict):"""F代表预测错了，N表示预测结果是Positive"""return np.sum((y_true==0)&(y_predict==1))return TP(y_true, y_predict)/(TP(y_true, y_predict)+FP(y_true,y_predict))#********* End *********#def recall_score(y_true, y_predict):'''计算召回率并召回:param y_true: 真实类别，类型为ndarray:param y_predict: 预测类别，类型为ndarray:return: 召回率，类型为float'''#********* Begin *********#def TP(y_true, y_predict):"""代表真实类别是Positive，预测结果也是Positive的数量"""return np.sum((y_true==1)&(y_predict==1))def FN(y_true,y_predict):"""F代表预测错了，N表示预测结果是Negative"""return np.sum((y_true==1)&(y_predict==0))return TP(y_true, y_predict)/(TP(y_true, y_predict)+FN(y_true,y_predict))#********* End *********#

F1 Score

如果想要同时兼顾精准率和召回率，可以使用F1 Score可以看成是模型准确率和召回率的一种加权平均，最大值是1，最小值是0.

ROC曲线与AUC

ROC曲线

ROC曲线描述TPR（召回率）和FPR之间的关系

若将 FPR 作为横轴， TPR 作为纵轴，将上面的表格以折线图的形式画出来就是 ROC曲线 

假设现在有模型 A 和模型 B ，它们的 ROC 曲线如下图所示(其中模型 A 的 ROC曲线 为黄色，模型 B 的 ROC 曲线 为蓝色)：

那么模型 A 的性能比模型 B 的性能好，因为模型 A 当 FPR 较低时所对应的 TPR 比模型 B 的低 FPR 所对应的 TPR 更高。由由于随着 FPR 的增大， TPR 也会增大。所以 ROC 曲线与横轴所围成的面积越大，模型的分类性能就越高。而 ROC曲线 的面积称为AUC。

AUC

import numpy as npdef calAUC(prob, labels):'''计算AUC并返回:param prob: 模型预测样本为Positive的概率列表，类型为ndarray:param labels: 样本的真实类别列表，其中1表示Positive，0表示Negative，类型为ndarray:return: AUC，类型为float'''#********* Begin *********#f = list(zip(prob, labels))# 按概率从小到大排序，默认升序排列f.sort(key=lambda x: x[0])# 给每个样本打排名，从1开始n = len(f)rank = np.arange(1, n+1)# 提取所有正负样本的索引pos_ranks = [rank[i] for i in range(n) if f[i][1] == 1]M = sum(labels)N = len(labels) - Mif M == 0 or N == 0:# 无法定义AUC（只有正或负样本）return 0.0# 计算正样本的平均排名auc = (np.sum(pos_ranks) - M * (M + 1) / 2) / (M * N)return auc#********* End *********#

sklearn中的分类性能指标

accu\fracy_score；
precision_score；
recall_score；
f1_score；
roc_auc_score。

import numpy as np
from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score, roc_auc_score# 模拟的真实标签（y_true）和模型预测
# y_true 是实际的分类结果，y_pred 是模型给出的分类标签（0 或 1）
# y_prob 是模型预测为正类（1）的概率，用于 AUC
y_true = np.array([0, 1, 1, 0, 1, 0, 1, 0])
y_pred = np.array([0, 1, 1, 0, 0, 0, 1, 1])     # 二分类标签
y_prob = np.array([0.2, 0.9, 0.8, 0.1, 0.4, 0.3, 0.7, 0.6])  # 预测为正类的概率# 1. 准确率（Accuracy）：预测正确的样本数占总样本数的比例
acc = accuracy_score(y_true, y_pred)# 2. 精确率（Precision）：预测为正类中有多少是真正的正类（减少“误杀”）
precision = precision_score(y_true, y_pred)# 3. 召回率（Recall）：所有实际正类中，被正确预测为正类的比例（减少“漏检”）
recall = recall_score(y_true, y_pred)# 4. F1 值：精确率和召回率的调和平均数，用于评价模型整体能力
f1 = f1_score(y_true, y_pred)# 5. ROC AUC 值：衡量模型对正负样本的排序能力，需要概率形式的预测
auc = roc_auc_score(y_true, y_prob)# 输出所有指标
print(f"Accuracy       : {acc:.4f}")
print(f"Precision      : {precision:.4f}")
print(f"Recall         : {recall:.4f}")
print(f"F1 Score       : {f1:.4f}")
print(f"ROC AUC Score  : {auc:.4f}")

广义线性模型

机器学习——线性回归

简单线性回归与多元线性回归

2、若线性回归方程得到多个解，下面哪些方法能够解决此问题？
A、获取更多的训练样本
B、选取样本有效的特征，使样本数量大于特征数
C、加入正则化项
D、不考虑偏置项b

A B C

3、下列关于线性回归分析中的残差（预测值减去真实值）说法正确的是？
A、残差均值总是为零
B、残差均值总是小于零
C、残差均值总是大于零
D、以上说法都不对

A 

在线性回归模型中（带有截距项），在最小二乘解下，有一个很重要的性质：

✅ 残差的平均值为 0

机器学习——感知机

感知机 - 西瓜好坏自动识别

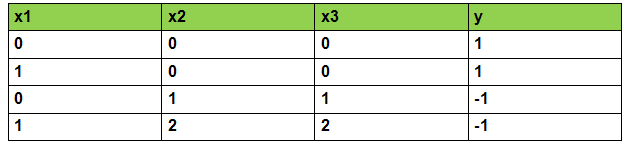
一共构造了帮助预测的特征一共有 30 个：色泽、根蒂、敲声等等。类别为是好瓜与不是好瓜。

由于当前模型只能对数字进行计算，所以用x1表示色泽（0表示青绿），x2表示根蒂（2表示稍蜷），x3表示敲声 。y 表示类别（-1，表示不是好瓜）。 

什么是感知机

感知机和逻辑回归一样，也是一个二分类模型

感知机的算法流程

我们能否正确对西瓜好坏进行预测，完全取决于权重与偏置的值是否正确，那么如何找到正确的参数呢？方法与逻辑回归相似，这里就不重复叙述，唯一不同的就是感知机模型所用的损失函数。

使用公式来实现感知机的代码如下所示，感觉就是公式的复现

#encoding=utf8
import numpy as np# 构建感知机算法
class Perceptron(object):def __init__(self, learning_rate=0.01, max_iter=200):self.lr = learning_rate      # 学习率（步长）self.max_iter = max_iter    # 最大训练轮数def fit(self, data, label):'''input:data(ndarray): 训练数据特征，形状是 (样本数量, 特征数量)label(ndarray): 每个样本对应的标签，取值通常是 1 或 -1output:self.w(ndarray): 学到的权重向量self.b(ndarray): 学到的偏置项'''# 初始化权重 w（每个特征一个权重），起始值全为 1self.w = np.array([1.0] * data.shape[1])# 初始化偏置 b 为 1self.b = 1.0# 感知机训练过程（迭代 max_iter 次）for _ in range(self.max_iter):for i in range(data.shape[0]):  # 遍历每一条训练样本x = data[i]                 # 当前样本的特征向量（形状如 [x1, x2, ..., xd]）y = label[i]               # 当前样本的标签（1 或 -1）# 计算模型对当前样本的预测值：w·x + bresult = np.dot(self.w, x) + self.b# 如果预测结果与标签不一致（即 y * result <= 0），说明分类错了if y * result <= 0:# 更新权重和偏置（感知机学习规则）self.w = self.w + self.lr * y * xself.b = self.b + self.lr * y# 训练完成后，self.w 和 self.b 就是学到的模型参数def predict(self, data):'''input:data(ndarray): 测试数据（若干样本）output:predict(ndarray): 模型预测的标签结果（1 或 -1）'''# 计算所有样本的预测值 w·x + b，并根据符号判断正负类result = np.dot(data, self.w) + self.b  # 每一行一个样本# 如果结果大于 0 就预测为 1， 否则为 -1predict = np.where(result > 0, 1, -1)return predict

使用sklearn

# encoding=utf8
import os
import pandas as pd
from sklearn.linear_model import Perceptron# 删除旧的结果文件（如果存在）
result_path = './step2/result.csv'
if os.path.exists(result_path):os.remove(result_path)# ===================== 1. 加载数据 ===================== ## 读取训练集特征
train_data = pd.read_csv('./step2/train_data.csv')# 读取训练集标签，并提取 target 列
train_label_df = pd.read_csv('./step2/train_label.csv')
train_label = train_label_df['target']# 读取测试集特征
test_data = pd.read_csv('./step2/test_data.csv')# ===================== 2. 训练模型 ===================== ## 创建 Perceptron（感知机）模型，设置学习率和迭代次数
model = Perceptron(eta0=0.01, max_iter=200)# 在训练集上拟合模型
model.fit(train_data, train_label)# ===================== 3. 生成预测结果 ===================== ## 使用模型对测试集进行预测
predictions = model.predict(test_data)# 将结果保存为 DataFrame
result_df = pd.DataFrame({'result': predictions})# 写入 CSV 文件
result_df.to_csv(result_path, index=False)

机器学习——多分类学习

OvO多分类策略

假设现在训练数据集的分布如下图所示，A B C代表训练数据的类别

如果想要使用逻辑回归算法来解决这种3分类问题，可以使用OvO。

OVO是使用二分类算法来解决多分类问题的一种策略。从字面上看它的核心思想就是一对一。所谓的“一”，指的是类别。而“对”指的是从训练集中划分不同的两个类别的组合来训练出多个分类器。

划分规则其实就是从原本的一一选出来，二分类

在预测阶段，只需要将测试样本分别扔给训练阶训练好的三个分类器进行预测，最后将三个分类器预测出的结果进行投票统计，票数最高的结果为预测结果。

这个代码主要是数据形式我没绕明白

import numpy as np# 逻辑回归
class tiny_logistic_regression(object):def __init__(self):#Wself.coef_ = None#bself.intercept_ = None#所有的W和bself._theta = None#01到标签的映射self.label_map = {}def _sigmoid(self, x):return 1. / (1. + np.exp(-x))#训练，train_labels中的值可以为任意数值def fit(self, train_datas, train_labels, learning_rate=1e-4, n_iters=1e3):#lossdef J(theta, X_b, y):y_hat = self._sigmoid(X_b.dot(theta))try:return -np.sum(y*np.log(y_hat)+(1-y)*np.log(1-y_hat)) / len(y)except:return float('inf')# 算theta对loss的偏导def dJ(theta, X_b, y):return X_b.T.dot(self._sigmoid(X_b.dot(theta)) - y) / len(y)# 批量梯度下降def gradient_descent(X_b, y, initial_theta, leraning_rate, n_iters=1e2, epsilon=1e-6):theta = initial_thetacur_iter = 0while cur_iter < n_iters:gradient = dJ(theta, X_b, y)last_theta = thetatheta = theta - leraning_rate * gradientif (abs(J(theta, X_b, y) - J(last_theta, X_b, y)) < epsilon):breakcur_iter += 1return thetaunique_labels = list(set(train_labels))labels = np.array(train_labels)# 将标签映射成0，1self.label_map[0] = unique_labels[0]self.label_map[1] = unique_labels[1]for i in range(len(train_labels)):if train_labels[i] == self.label_map[0]:labels[i] = 0else:labels[i] = 1X_b = np.hstack([np.ones((len(train_datas), 1)), train_datas])initial_theta = np.zeros(X_b.shape[1])self._theta = gradient_descent(X_b, labels, initial_theta, learning_rate, n_iters)self.intercept_ = self._theta[0]self.coef_ = self._theta[1:]return self#预测X中每个样本label为1的概率def predict_proba(self, X):X_b = np.hstack([np.ones((len(X), 1)), X])return self._sigmoid(X_b.dot(self._theta))#预测def predict(self, X):proba = self.predict_proba(X)result = np.array(proba >= 0.5, dtype='int')# 将0，1映射成标签for i in range(len(result)):if result[i] == 0:result[i] = self.label_map[0]else:result[i] = self.label_map[1]return resultclass OvO(object):def __init__(self):# 用于保存训练时各种模型的listself.models = []def fit(self, train_datas, train_labels):'''OvO的训练阶段，将模型保存到self.models中:param train_datas: 训练集数据，类型为ndarray:param train_labels: 训练集标签，标签值为0,1,2之类的整数，类型为ndarray，shape为(-1,):return:None'''#********* Begin *********#unique_classes = np.unique(train_labels)#为每一对不同类别都训练一个模型for i in range(len(unique_classes)):for j in range(i+1,len(unique_classes)):class_i = unique_classes[i]class_j = unique_classes[j]#选出属于这两个类别的样本idx = np.where((train_labels == class_i) | (train_labels == class_j))[0]binary_X = train_datas[idx]binary_y = train_labels[idx]#训练一个二分类器model = tiny_logistic_regression()model.fit(binary_X, binary_y)self.models.append((model,class_i,class_j))#********* End *********#def predict(self, test_datas):'''OvO的预测阶段:param test_datas:测试集数据，类型为ndarray:return:预测结果，类型为ndarray'''#********* Begin *********#n_samples = test_datas.shape[0] #样本数量votes = [{} for _ in range(n_samples)]  # 每个样本一个投票箱# votes = [{}, {}, {}, {}, {}]#第二步：遍历每个模型，对每个样本投票# model_0_1.predict(test_datas) = [0, 1, 1, 0, 0]# model_0_2.predict(test_datas) = [0, 0, 2, 2, 0]# model_1_2.predict(test_datas) = [2, 1, 2, 2, 1]for model, class_i, class_j in self.models:preds = model.predict(test_datas)# [0, 1, 1, 0, 0]for idx in range(n_samples):pred_label = preds[idx]if pred_label not in votes[idx]:votes[idx][pred_label] = 0 #初始化votes[idx][pred_label] += 1#votes会更新# votes = [#     {0:1},        # 第1个样本投给0#     {1:1},        # 第2个投给1#     {1:1},        # 第3个投给1#     {0:1},        # 第4个投给0#     {0:1},        # 第5个投给0# ]# votes = [#     {0:2},            # 又投了0#     {1:1, 0:1},       # 又投了0#     {1:1, 2:1},       # 投了2#     {0:1, 2:1},       # 投了2#     {0:2},            # 又投了0# ]# 最终预测为票数最多的类别final_preds = np.zeros(n_samples, dtype=int)for i in range(n_samples):# .items() 是字典中所有 (类, 票数) 对，比如 {0: 2, 2: 1} → [(0, 2), (2, 1)]sorted_votes = sorted(votes[i].items(), key=lambda x: x[1], reverse=True)final_preds[i] = sorted_votes[0][0]return final_preds#********* End *********#

OvR多分类策略

如果想要使用逻辑回归算法来解决这种3分类问题，可以使用OvR。OvR(One Vs Rest)是使用二分类算法来解决多分类问题的一种策略。从字面意思可以看出它的核心思想就是一对剩余。一对剩余的意思是当要对n种类别的样本进行分类时，分别取一种样本作为一类，将剩余的所有类型的样本看做另一类，这样就形成了n个二分类问题。所以和OvO一样，在训练阶段需要进行划分。

分别用这3种划分，划分出来的训练集训练二分类分类器，就能得到3个分类器。此时训练阶段已经完毕。如下图所示：

在预测阶段，只需要将测试样本分别扔给训练阶段训练好的3个分类器进行预测，最后选概率最高的类别作为最终结果。

仍然绕不清楚，这个数据的具体的形式，感觉得系统学一遍numpy

import numpy as np
# 逻辑回归
class tiny_logistic_regression(object):def __init__(self):#Wself.coef_ = None#bself.intercept_ = None#所有的W和bself._theta = None#01到标签的映射self.label_map = {}def _sigmoid(self, x):return 1. / (1. + np.exp(-x))#训练def fit(self, train_datas, train_labels, learning_rate=1e-4, n_iters=1e3):#lossdef J(theta, X_b, y):y_hat = self._sigmoid(X_b.dot(theta))try:return -np.sum(y*np.log(y_hat)+(1-y)*np.log(1-y_hat)) / len(y)except:return float('inf')# 算theta对loss的偏导def dJ(theta, X_b, y):return X_b.T.dot(self._sigmoid(X_b.dot(theta)) - y) / len(y)# 批量梯度下降def gradient_descent(X_b, y, initial_theta, leraning_rate, n_iters=1e2, epsilon=1e-6):theta = initial_thetacur_iter = 0while cur_iter < n_iters:gradient = dJ(theta, X_b, y)last_theta = thetatheta = theta - leraning_rate * gradientif (abs(J(theta, X_b, y) - J(last_theta, X_b, y)) < epsilon):breakcur_iter += 1return thetaX_b = np.hstack([np.ones((len(train_datas), 1)), train_datas])initial_theta = np.zeros(X_b.shape[1])self._theta = gradient_descent(X_b, train_labels, initial_theta, learning_rate, n_iters)self.intercept_ = self._theta[0]self.coef_ = self._theta[1:]return self#预测X中每个样本label为1的概率def predict_proba(self, X):X_b = np.hstack([np.ones((len(X), 1)), X])return self._sigmoid(X_b.dot(self._theta))#预测def predict(self, X):proba = self.predict_proba(X)result = np.array(proba >= 0.5, dtype='int')return result
class OvR(object):def __init__(self):# 用于保存训练时各种模型的listself.models = []# 用于保存models中对应的正例的真实标签# 例如第1个模型的正例是2，则real_label[0]=2self.real_label = []def fit(self, train_datas, train_labels):'''OvO的训练阶段，将模型保存到self.models中:param train_datas: 训练集数据，类型为ndarray:param train_labels: 训练集标签，类型为ndarray，shape为(-1,):return:None'''#********* Begin *********#unique_classes = np.unique(train_labels)  # 获取所有不同的类，例如：[0, 1, 2]for cls in unique_classes:binary_labels = np.array(train_labels == cls,dtype = int)# 例：当 cls=1，train_labels = [0, 1, 2, 1, 0]# 则 binary_labels = [0, 1, 0, 1, 0]model = tiny_logistic_regression()model.fit(train_datas, binary_labels)self.models.append(model)self.real_label.append(cls)#********* End *********#def predict(self, test_datas):'''OvR的预测阶段:param test_datas:测试集数据，类型为ndarray:return:预测结果，类型为ndarray'''#********* Begin *********#n_samples = test_datas.shape[0]n_classes = len(self.models)proba_matrix = np.zeros((n_samples, n_classes))  # 形如：(5, 3)for i in range(n_classes):model = self.models[i]# 对每个样本，预测“是类 real_label[i]”的概率proba_matrix[:, i] = model.predict_proba(test_datas)# 例如：# model 0 对 5 个样本预测结果为 [0.8, 0.2, 0.1, 0.3, 0.7]，则存入第0列# model 1 对 5 个样本预测结果为 [0.1, 0.7, 0.8, 0.4, 0.2]，则存入第1列# model 2 对 5 个样本预测结果为 [0.3, 0.1, 0.7, 0.6, 0.4]，则存入第2列# 示例：# proba_matrix = [#   [0.8, 0.1, 0.3],  # sample 0 → 0#   [0.2, 0.7, 0.1],  # sample 1 → 1#   [0.1, 0.8, 0.7],  # sample 2 → 1 (if 0.8 > 0.7)#   [0.3, 0.4, 0.6],  # sample 3 → 2#   [0.7, 0.2, 0.4],  # sample 4 → 0# ]best_class_indices = np.argmax(proba_matrix, axis=1)final_preds = np.array([self.real_label[i] for i in best_class_indices])return final_preds#********* End *********#

机器学习 --- kNN算法

实现kNN算法

“近朱者赤近墨者黑”

numpy实现投票计数

1.计算欧氏距离（L2范数）

2.选择 k 个最近邻

3.统计 k 个邻居的标签

4.将多数类作为预测结果

#encoding=utf8
import numpy as npclass kNNClassifier(object):def __init__(self, k):'''初始化函数:param k:kNN算法中的k'''self.k = k# 用来存放训练数据，类型为ndarrayself.train_feature = None# 用来存放训练标签，类型为ndarrayself.train_label = Nonedef fit(self, feature, label):'''kNN算法的训练过程:param feature: 训练集数据，类型为ndarray:param label: 训练集标签，类型为ndarray:return: 无返回'''#********* Begin *********#self.train_feature = featureself.train_label = label#********* End *********#def predict(self, feature):'''kNN算法的预测过程:param feature: 测试集数据，类型为ndarray:return: 预测结果，类型为ndarray或list'''#********* Begin *********#pred = []for i in feature:#计算每个测试点与所有训练点的欧式距离dist = np.linalg.norm(self.train_feature-i,axis=1)#找出距离最近的k个训练点索引k_idx = np.argsort(dist)[:self.k]#获取这k个训练点的标签k_labels = self.train_label[k_idx]#多数投票val,cnt = np.unique(k_labels,return_counts=True)majority_label = val[np.argmax(cnt)]pred.append(majority_label)return np.array(pred)#********* End *********#

红酒分类sklearn实现即可

StandardScaler的使用

由于数据中有些特征的标准差比较大，例如 Proline 的标准差大约为 314。如果现在用 kNN 算法来对这样的数据进行分类的话， kNN 算法会认为最后一个特征比较重要。因为假设有两个样本的最后一个特征值分别为 1 和 100，那么这两个样本之间的距离可能就被这最后一个特征决定了。这样就很有可能会影响 kNN 算法的准确度。为了解决这种问题，我们可以对数据进行标准化。

标准化的手段有很多，而最为常用的就是 Z Score 标准化。Z Score 标准化通过删除平均值和缩放到单位方差来标准化特征，并将标准化的结果的均值变成 0 ，标准差为 1。

sklearn 中已经提供了 Z Score 标准化的接口 StandardScaler

计算均值和标准差，并进行标准化（fit + transform）

使用场景：

特征分布差异大的时候；SVM、KNN、逻辑回归、神经网络等

不能用于异常值特别多的数据（因为标准差对异常值敏感）

方法	作用
fit(data)	计算均值和标准差
transform(data)	根据已有均值和标准差标准化数据
fit_transform(data)	连续执行 fit + transform
inverse_transform(data)	还原标准化前的数据（反标准化）

from sklearn.preprocessing import StandardScaler
data = [[0, 0], [0, 0], [1, 1], [1, 1]]
# 实例化StandardScaler对象
scaler = StandardScaler()
# 用data的均值和标准差来进行标准化，并将结果保存到after_scaler
after_scaler = scaler.fit_transform(data)
#相当于两步，也就是scaler.fit(data)           # 计算每一列的均值和标准差
#  after_scaler = scaler.transform(data)  # 用均值和标准差标准化 data# 用刚刚的StandardScaler对象来进行归一化
after_scaler2 = scaler.transform([[2, 2]])
print(after_scaler)
print(after_scaler2)

参数名	说明	类型	默认值	备注
n_neighbors	kNN算法中的K值，表示选取几个最近邻进行投票	int	5	一般根据数据集调节
metric	距离度量方法	str 或 callable	'minkowski'	可选如 'euclidean', 'manhattan'等
p	当metric='minkowski'时使用的参数，表示距离的阶数	int	2	p=2为欧氏距离，p=1为曼哈顿距离
weights	预测时邻居权重	str 或 callable	'uniform'	'uniform'(均等权重), 'distance'(距离倒数权重)
algorithm	用于计算最近邻的算法	str	'auto'	'auto', 'ball_tree', 'kd_tree', 'brute'
n_jobs	并行运行的作业数	int	1	-1为使用所有处理器

from sklearn.neighbors import KNeighborsClassifier
from sklearn.preprocessing import StandardScalerdef classification(train_feature, train_label, test_feature):'''对test_feature进行红酒分类:param train_feature: 训练集数据，类型为ndarray:param train_label: 训练集标签，类型为ndarray:param test_feature: 测试集数据，类型为ndarray:return: 测试集数据的分类结果'''#********* Begin *********#scaler = StandardScaler()train = scaler.fit_transform(train_feature)test = scaler.transform(test_feature)   # 注意这里不是 fit_transform！knn = KNeighborsClassifier()knn.fit(train, train_label)predict_result = knn.predict(test)return predict_result#********* End **********#

机器学习 --- 决策树

什么是决策树

决策树是一种可以用于分类与回归的机器学习算法，但是主要用于分类。用于分类的决策树是一种描述对实例进行分类的树形结构。决策树由结点和边组成，其中结点分为内部结点和叶子结点，内部结点表示一个特征或者属性，叶子结点表示标签。

如何构建出一棵好的决策树呢？

构造决策树的时候会遵循一个指标，
有的是按照信息增益来构建，如ID3算法；
有的是信息增益率来构建，如C4.5算法；
有的是按照基尼系数来构建的，如CART算法。

信息熵与信息增益

信息熵

热力学中的热熵是表示分子状态混乱程度的物理量。香农用信息熵的概念来描述信源的不确定度。信源的不确定性越大，信息熵也越大。

从机器学习的角度来看，信息熵表示的是信息量的期望值。

从这个公式可以看出，如果概率是0或1的时候，熵就是0（因为这种情况下随机变量的不确定性是最低的）。但如果概率是0.5，熵最大。故，熵越大，不确定性越高。

条件熵

在实际的场景中，我们可能需要研究数据集中某个特征等于某个值时的信息熵等于多少，这个时候就需要用到条件熵。条件熵H(Y|X)表示特征X为某个值的条件下，类别为Y的熵。条件熵的计算公式如下：

信息增益

信息增益就是表示我已知条件X后能得到信息Y的不确定性的减少程度。

所以信息增益如果套上机器学习的话就是，如果把特征A对训练集D的信息增益记为g(D, A)的话，那么g(D, A)的计算公式就是

那信息增益算出来之后有什么意义呢？回到读心术的问题，为了我能更加准确的猜出你心中所想，我肯定是问的问题越好就能猜得越准！换句话来说我肯定是要想出一个信息增益最大（减少不确定性程度最高）的问题来问你。其实ID3算法也是这么想的。ID3算法的思想是从训练集D中计算每个特征的信息增益，然后看哪个最大就选哪个作为当前结点。然后继续重复刚刚的步骤来构建决策树。

机器学习 --- 支持向量回归(SVR)

线性可分支持向量机

线性二分类问题

图中的绿线和黄线都能很好的将图中的红点和蓝点区分开来，但是哪条线的泛化性更好呢？也就是这条直线不仅需要在训练集（已知的数据） 上能够很好的将红点跟蓝点区分开来，还要在测试集（未知的数据） 上将红点跟蓝点给区分开来。

假如经过训练，我们得到了黄色的这条决策边界用来区分我们的数据，这个时候又来了一个数据，即黑色的点，如上图，根据黄线的划分标准，黑色的点应该属于红色这一类。可是，我们肉眼很容易发现，黑点离蓝色的点更近，它应该是属于蓝色的点。这就说明，黄色的这条直线它的泛化性并不好，它对于未知的数据并不能很好的进行分类。那么，如何得到一条泛化性好的直线呢？这个就是支持向量机考虑的问题。

基本思想

支持向量机的思想认为，一条决策边界乳香要有很好的泛化性，需要满足以下两个条件：

1.能够很好的将样本划分
2.离最近的样本点最远

无论新的数据出现在哪个位置，决策边界都能够很好的给它进行分类，这个就是支持向量机的基本思想。

间隔与支持向量

如图中，距离最近的几个点使两个不等式的等号成立，它们就被称为支持向量，即图中两条黄色的线。两个异类支持向量到超平面的距离之和为：r= 2/||w||，这被称为间隔，也就是蓝色的线的长度。想要找到最大间隔的决策边界，也就是黑色的线，也就是要找到能够同时满足如下式子的w与b:
​

支持向量机的最终模型仅仅与支持向量有关。支持向量机的最终模型由离决策边界最近的几个点决定。

线性支持向量机

软间隔

 按照线性可分支持向量机的思想，黄色的线就是最佳的决策边界。很明显，这条线的泛化性不是很好，造成这样结果的原因就是数据中存在着异常点，那么如何解决这个问题呢，支持向量机引入了软间隔最大化的方法来解决。

# 线性的
from sklearn.svm import LinearSVCdef linearsvc_predict(train_data,train_label,test_data):'''input:train_data(ndarray):训练数据train_label(ndarray):训练标签output:predict(ndarray):测试集预测标签'''#********* Begin *********# clf = LinearSVC(dual=False)clf.fit(train_data,train_label)predict = clf.predict(test_data)#********* End *********# return predict

非线性支持向量机

非线性的

from sklearn.svm import SVCdef svc_predict(train_data,train_label,test_data,kernel):'''input:train_data(ndarray):训练数据train_label(ndarray):训练标签kernel(str):使用核函数类型:'linear':线性核函数'poly':多项式核函数'rbf':径像核函数/高斯核output:predict(ndarray):测试集预测标签'''#********* Begin *********# clf = SVC(kernel=kernel)clf.fit(train_data,train_label)predict=clf.predict(test_data)#********* End *********# return predict

机器学习 --- Adaboost

Boosting

什么是集成学习

集成学习方法是一种常用的机器学习方法，分为 bagging 与 boosting 两种方法

集成学习基本思想是：对于一个复杂的学习任务，我们首先构造多个简单的学习模型，然后再把这些简单模型组合成一个高效的学习模型。实际上，就是“三个臭皮匠顶个诸葛亮”的道理。

集成学习采取投票的方式来综合多个简单模型的结果，按 bagging 投票思想，如下面例子：

 假设一共训练了 5 个简单模型，每个模型对分类结果预测如上图，则最终预测结果为：投票最多的B

不过在有的时候，每个模型对分类结果的确定性不一样，即有的对分类结果非常肯定，有的不是很肯定,说明每个模型投的一票应该是有相应的权重来衡量这一票的重要性。就像在歌手比赛中，每个观众投的票记 1 分，而专家投票记 10 分。按 boosting 投票思想，如下例：

A：(0.9+0.4+0.3+0.8+0.2)/5=0.52
B：(0.1+0.6+0.7+0.2+0.8)/5=0.48
0.52>0.48
结果为 A

Boosting

提升方法基于这样一种思想：对于一个复杂任务来说，将多个专家的判断进行适当综合所得出的判断，要比其中任何一个专家单独的判断好。

与bagging不同，Boosting采用的是一个串行训练的方法。首先，它训练出一个弱分类器，然后在此基础上，再训练出一个稍好点的弱分类器，以此类推，不断的训练出多个弱分类器，最终再将这些分类器相结合，这就是 boosting 的基本思想。

可以看出，子模型之间存在强依赖关系，必须串行生成。 boosting 是利用不同模型的相加，构成一个更好的模型，求取模型一般都采用序列化方法，后面的模型依据前面的模型。

Adaboost算法

Adaboost算法原理

对提升方法来说，有两个问题需要回答：一是在每一轮如何改变训练数据的权值或概率分布；二是如何将弱分类器组合成一个强分类器。关于第 1 个问题，AdaBoost的做法是，提高那些被前一轮弱分类器错误分类样本的权值，而降低那些被正确分类样本的权值。这样一来，那些没有得到正确分类的数据，由于其权值的加大而受到后一轮的弱分类器的更大关注。于是，分类问题被一系列的弱分类器“分而治之”。至于第 2 个问题，即弱分类器的组合，AdaBoost采取加权多数表决的方法，加大分类误差率小的弱分类器的权值，使其在表决中起较大的作用，减小分类误差率大的弱分类器的权值，使其在表决中起较小的作用。

sklearn中的Adaboost

AdaBoostClassifier

 AdaBoostClassifier 的构造函数中有四个常用的参数可以设置：

algorithm ：这个参数只有 AdaBoostClassifier 有。主要原因是scikit-learn 实现了两种 Adaboost 分类算法， SAMME 和 SAMME.R。两者的主要区别是弱学习器权重的度量， SAMME.R 使用了概率度量的连续值，迭代一般比 SAMME 快，因此 AdaBoostClassifier 的默认算法 algorithm 的值也是 SAMME.R；

 n_estimators ：弱学习器的最大迭代次数。一般来说 n_estimators 太小，容易欠拟合，n_estimators 太大，又容易过拟合，一般选择一个适中的数值。默认是 50；

 learning_rate ：AdaBoostClassifier 和 AdaBoostRegressor 都有，即每个弱学习器的权重缩减系数 ν，默认为 1.0；

 base_estimator ：弱分类学习器或者弱回归学习器。理论上可以选择任何一个分类或者回归学习器，不过需要支持样本权重。我们常用的一般是 CART 决策树或者神经网络 MLP。

和 sklearn 中其他分类器一样，AdaBoostClassifier 类中的 fit 函数用于训练模型，fit 函数有两个向量输入：

 X ：大小为**[样本数量,特征数量]**的 ndarray，存放训练样本；

 Y ：值为整型，大小为**[样本数量]**的 ndarray，存放训练样本的分类标签。

from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import AdaBoostClassifier
def ada_classifier(train_data,train_label,test_data):'''input:train_data(ndarray):训练数据train_label(ndarray):训练标签test_data(ndarray):测试标签output:predict(ndarray):预测结果'''#********* Begin *********#ada=AdaBoostClassifier(n_estimators=500,learning_rate=0.5)ada.fit(train_data,train_label)predict = ada.predict(test_data)#********* End *********# return predict

感觉使用sklearn就是在调参……

机器学习之随机森林算法

Bagging

什么是 Bagging

Bagging 是 Bootstrap Aggregating 的英文缩写，刚接触的童鞋不要误认为 Bagging 是一种算法， Bagging 和 Boosting 都是集成学习中的学习框架，代表着不同的思想。与 Boosting 这种串行集成学习算法不同， Bagging 是并行式集成学习方法。大名鼎鼎的随机森林算法就是在 Bagging 的基础上修改的算法。

Bagging 方法的核心思想就是三个臭皮匠顶个诸葛亮。如果使用 Bagging 解决分类问题，就是将多个分类器的结果整合起来进行投票，选取票数最高的结果作为最终结果。如果使用 Bagging 解决回归问题，就将多个回归器的结果加起来然后求平均，将平均值作为最终结果。

Bagging 算法如何训练与预测

训练

Bagging 在训练时的特点就是随机有放回采样和并行。

随机有放回采样：假设训练数据集有 m 条样本数据，每次从这 m 条数据中随机取一条数据放入采样集，然后将其返回，让下一次采样有机会仍然能被采样。然后重复 m 次，就能得到拥有 m 条数据的采样集，该采样集作为 Bagging 的众多分类器中的一个作为训练数据集。假设有 T 个分类器（随便什么分类器），那么就重复 T 此随机有放回采样，构建出 T 个采样集分别作为 T 个分类器的训练数据集。

并行：假设有 10 个分类器，在 Boosting 中，1 号分类器训练完成之后才能开始 2 号分类器的训练，而在 Bagging 中，分类器可以同时进行训练，当所有分类器训练完成之后，整个 Bagging 的训练过程就结束了。

Bagging 训练过程如下图所示：

预测

Bagging 在预测时非常简单，就是投票！比如现在有 5 个分类器，有 3 个分类器认为当前样本属于 A 类，1 个分类器认为属于 B 类，1 个分类器认为属于 C 类，那么 Bagging 的结果会是 A 类（因为 A 类的票数最高）。

后续的算法的具体实现有时间就做吧，没时间的话记忆一下概念。