【机器学习】支持向量回归(SVR)从入门到实战:原理、实现与优化指南
前言
在机器学习的广阔领域中,回归分析作为预测连续型变量的重要手段,被广泛应用于金融预测、工业生产、科学研究等诸多场景。支持向量回归(SVR)作为回归算法家族中的佼佼者,凭借独特的理论优势与强大的实践能力脱颖而出。它基于支持向量机(SVM)的思想,创新性地引入 ε- 不敏感带,有效平衡模型复杂度与泛化能力,尤其在处理非线性问题时展现出卓越性能。

本文将从理论到实践,系统且深入地剖析 SVR。不仅会阐述其核心概念、数学原理,还会通过具体的代码实现,展示从数据预处理、模型训练调参到评估优化的完整流程,助力读者全面掌握这一实用的机器学习算法。
1. SVR基础概念与核心原理
1.1 什么是SVR?
支持向量回归(Support Vector Regression, SVR)是基于支持向量机(SVM)的回归模型,旨在通过寻找最优超平面来预测连续型变量。与传统回归方法不同,SVR允许数据点在ε-不敏感带内存在误差,从而平衡模型复杂度与泛化能力。
1.2 SVR与SVM的区别
- 目标差异:SVM用于分类,而SVR处理回归问题,通过最大化间隔超平面与数据点的距离来拟合连续值。
- 损失函数:SVR采用ε-不敏感损失函数,对误差在±ε范围内的数据点不进行惩罚,仅关注超出该范围的误差。
1.3 数学原理解析
优化目标:
SVR的目标函数为最小化权重向量的范数和松弛变量惩罚项:
min 1 2 ∥ w ∥ 2 + C ∑ i = 1 n ( ξ i + ξ i ∗ ) \min \frac{1}{2}\|w\|^2 + C\sum_{i=1}^n (\xi_i + \xi_i^*) min21∥w∥2+Ci=1∑n(ξi+ξi∗)
约束条件确保预测值与真实值的偏差不超过ε,其中C为惩罚系数,控制模型复杂性与误差容忍度。
目标函数和最小二乘法:
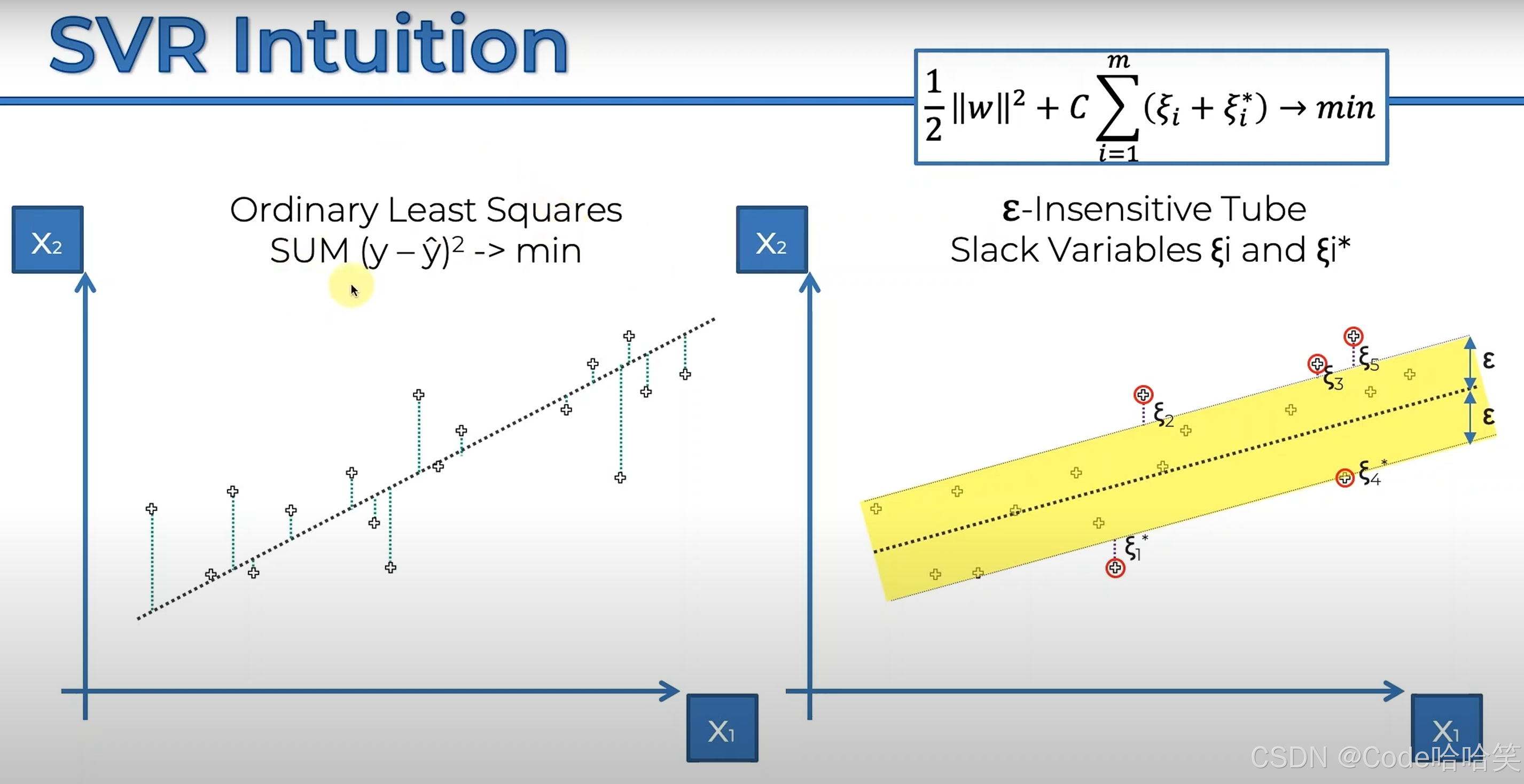
左边是用最小二乘法求得的直线;右边是用目标函数求得的SVR模型,黄色区域是值的是正确的范围,也叫做 ε(误差容忍度),黄色外面的是误差较大的值,也叫做支持向量,决定着SVR模型,所以该模型叫做支持向量回归。
支持向量如下图(与原点连接)。

核函数的作用:
通过核技巧(如RBF、多项式核)将数据映射到高维空间,解决非线性问题。例如,径向基核(RBF)的表达式为:
K ( x i , x j ) = exp ( − γ ∥ x i − x j ∥ 2 ) K(x_i, x_j) = \exp\left(-\gamma \|x_i - x_j\|^2\right) K(xi,xj)=exp(−γ∥xi−xj∥2)
2. SVR建模全流程实现
2.1 数据准备与预处理
- 数据标准化:使用
MinMaxScaler或StandardScaler对特征和标签归一化:
from sklearn.preprocessing import MinMaxScaler
mm1 = MinMaxScaler()
X_train_scaled = mm1.fit_transform(X_train)
2.2 模型训练与调参
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
说明:
- 通过random_state参数设置随机种子,确保每次划分结果一致,便于实验复现;
- test_size=0.2表示将20%的数据分配为测试集,80%作为训练集,进行保留独立测试集。
2.3模型训练与调参
from sklearn.svm import SVR
model = SVR(kernel='rbf', C=100, gamma=0.1, epsilon=0.2)
model.fit(X_train_scaled, y_train)
说明:
- kernel=‘rbf’(核函数):指定模型使用的核函数类型,rbf(径向基函数)适用于非线性回归问题
- C=100(正则化参数):控制对误差的惩罚强度。值越大(如C=100),模型对训练误差容忍度越低,可能提升拟合精度但增加过拟合风险
- gamma=0.1(核系数):决定单个样本对模型的影响范围。较小的gamma(如0.1)使核函数更平滑,模型泛化性更好;较大值易导致过拟合
- epsilon=0.2(不敏感带宽度):允许预测值与真实值的绝对误差不超过此阈值时不计算损失。epsilon=0.2表示容忍±0.2的偏差
通常的参数组合:
高C+低gamma:适合复杂非线性数据,但需警惕过拟合
2.3 模型评估与可视化
from sklearn.metrics import mean_squared_error, r2_score
# 将测试集输入模型中进行预测--得到预测值
y_pred = model.predict(X_test_scaled)#将真实值与预测值进行比较
mse = mean_squared_error(y_test, y_pred) #越小越好
r2 = r2_score(y_test, y_pred) #越接近1越好
mean_absolute_error = mean_absolute_error(y_test, y_pred) #越小越好
mean_absolute_percentage_error = mean_absolute_percentage_error(y_test, y_pred) #越小越好
说明:
-
MSE(均方误差)
计算公式: M S E = ( 1 / m ) ∗ Σ ( y i − y ^ i ) 2 MSE = (1/m) * Σ(y_i - ŷ_i)² MSE=(1/m)∗Σ(yi−y^i)2
作用:衡量预测值与真实值的平均平方偏差
特性:
(1)对异常值敏感(平方放大误差)
(2)适用于需严格惩罚大误差的场景(如金融预测) -
R²(决定系数)
计算公式: R 2 = 1 − ( S S r e s / S S t o t ) R² = 1 - (SS_res / SS_tot ) R2=1−(SSres/SStot)
解读:
(1) 值越接近1,模型拟合越好
(2)负数表示模型不如均值预测 -
MAE (平均绝对误差)
计算公式: M A E = ( 1 / m ) ∗ Σ ∣ y i − y ^ i ∣ MAE = (1/m) * Σ|y_i - ŷ_i| MAE=(1/m)∗Σ∣yi−y^i∣
特点:(1)比MSE更鲁棒,不受异常值平方放大影响
(2)与原始数据同量纲,更易解释
适用场景:需要直观理解平均误差时(如房价预测误差±5万元) -
MAPE (平均绝对百分比误差)
计算公式: M A P E = ( 1 / m ) ∗ Σ ∣ ( y i − y ^ i ) / y i ∣ ∗ 100 MAPE = (1/m) * Σ|(y_i - ŷ_i)/y_i| * 100% MAPE=(1/m)∗Σ∣(yi−y^i)/yi∣∗100
特点:
(1)结果以百分比表示,适合跨量纲比较
(3)当y_true有0值时失效
适用场景:需要相对误差评估(如销量预测误差±15%)
| 指标名称 | 最佳值 | 特点 | 适用场景 |
|---|---|---|---|
| MSE | 越小越好 | 强调大误差 | 需要严格惩罚大偏差 |
| MAE | 越小越好 | 直观易解释 | 业务汇报场景 |
| MAPE | 越小越好 | 百分比形式 | 跨量纲比较 |
| R² | 1 | 无量纲,解释力 | 学术论文/模型对比 |
| Explained Variance | 1 | 不考虑系统偏差 | 高精度建模场景 |
3. 参数优化与高级技巧
3.1 超参数调优方法
网格搜索:
from sklearn.model_selection import GridSearchCV# 网格搜索
param_grid = {'C': [1, 10, 100], # 正则化参数,控制模型对误差的惩罚强度'gamma': [0.01, 0.1, 1] # RBF核函数的系数,控制单个样本的影响范围}grid = GridSearchCV(estimator=SVR(), # 使用的模型(此处为支持向量回归)param_grid=param_grid, # 待搜索的参数组合cv=5 # 5折交叉验证
)grid.fit(X_train, y_train)
说明:
C参数:
值越大(如100)对训练误差惩罚越强,可能提高拟合精度但增加过拟合风险
值越小(如1)允许更多误差,模型更简单但可能欠拟合
gamma参数:
值越大(如1)核函数更"尖锐",模型对局部数据更敏感
值越小(如0.01)核函数更平滑,泛化能力更强
cv=5:将数据分为5份,轮流用4份训练、1份验证,重复5次
工作流程:
(1)自动遍历{‘C’:1, ‘gamma’:0.01}到{‘C’:100, ‘gamma’:1}共9种组合
(2)对每种组合进行5次交叉验证
(3)选择平均验证分数最高的参数组合
3.2 核函数选择策略
# 线性核
SVR(kernel='linear') # 多项式核(需指定阶数degree)
SVR(kernel='poly', degree=3, gamma='auto') # RBF核(默认)
SVR(kernel='rbf')
线性核:适用于线性可分场景
RBF核:默认选择,适合非线性问题
多项式核:需调整阶数参数
4. 总结
这篇博客围绕支持向量回归(SVR)展开,系统介绍了 SVR 的理论基础、建模流程、参数优化等内容,具体总结如下:
-
SVR 基础概念与核心原理
定义:SVR 是基于支持向量机(SVM)的回归模型,通过寻找最优超平面预测连续型变量,允许数据点在 ε- 不敏感带内存在误差,平衡模型复杂度与泛化能力。
与 SVM 的区别:SVM 用于分类,SVR 处理回归;SVR 采用 ε- 不敏感损失函数,仅惩罚超出 ε 范围的误差。
数学原理:目标函数为最小化权重向量范数和松弛变量惩罚项,通过核函数(如 RBF、多项式核)将数据映射到高维空间处理非线性问题。 -
SVR 建模全流程实现
数据准备与预处理:使用MinMaxScaler或StandardScaler对数据进行标准化。
模型训练与调参:通过train_test_split划分数据集,使用SVR类训练模型,需关注核函数、正则化参数C、核系数gamma、不敏感带宽度epsilon等参数对模型的影响。
模型评估与可视化:采用均方误差(MSE)、决定系数(R²)、平均绝对误差(MAE)、平均绝对百分比误差(MAPE)等指标评估模型性能,各指标适用于不同场景 。
参数优化与高级技巧 -
超参数调优方法:利用网格搜索(GridSearchCV)遍历参数组合,通过交叉验证选择最优参数,如C和gamma。
核函数选择策略:线性核适用于线性可分数据,RBF 核是处理非线性问题的默认选择,多项式核则需要调整阶数参数 。
