【机器学习】通过tensorflow搭建神经网络进行气温预测
搭建神经网络进行气温预测
简介
通过tensorflow搭建神经网络模型来探讨气温预测的回归问题,初步学习tensorflow。
导入库以及环境配置
加载数据处理(NumPy/Pandas)、可视化(Matplotlib)、建模(TensorFlow/Keras)所需的核心库,再配置环境以减少干扰,为后续的数据加载、探索性分析、模型训练等步骤做准备。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import tensorflow as tf
from tensorflow.keras import layers
import tensorflow.keras
import warnings
warnings.filterwarnings("ignore")
%matplotlib inline
读取 CSV 文件并预览数据
读取结构化数据文件并查看其前几行内容。
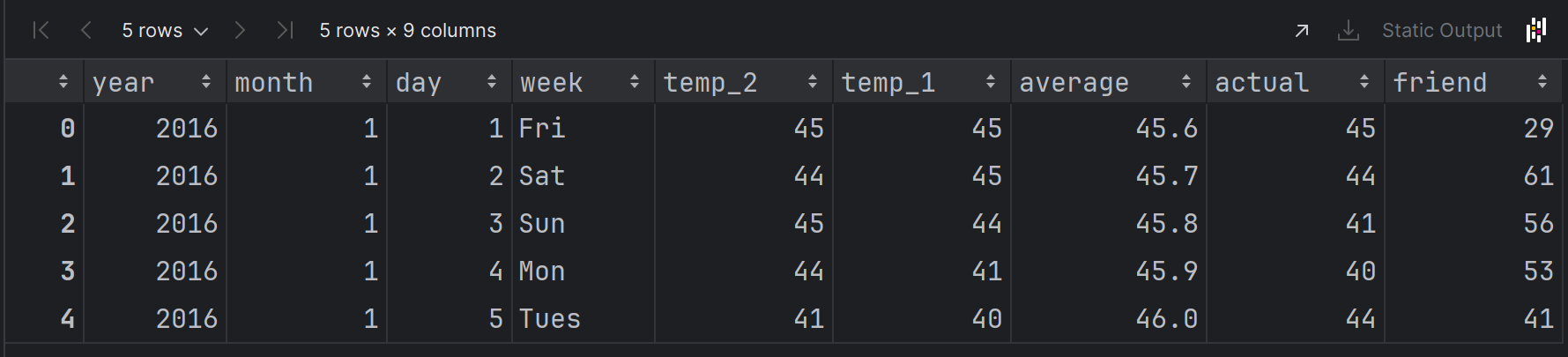
features = pd.read_csv('../temps.csv')
features.head()
数据展示
数据表中
- year,moth,day,week分别表示的具体时间
- temp_2前天的最高温度值
- temp_1昨天的最高温度值
- average在历史中每年这一天的平均最高温度值
- actual标签值,当天真实最高温度
- friend猜测的可能值,不用管
查看数据维度、处理时间数据
查看数据集的维度(即行数和列数),并将数据集中分散的 “年、月、日” 字段整合为标准的datetime时间格式,为后续时间序列分析做准备。
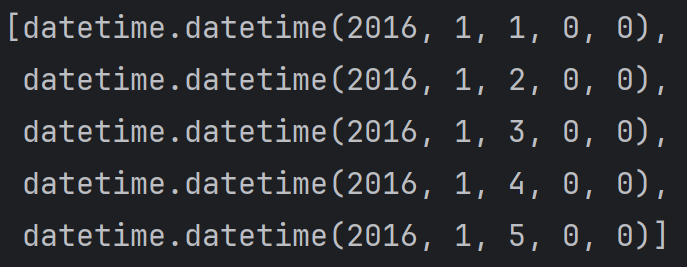
print('数据维度',features.shape)
# 处理时间数据
import datetime
# 分别得到年、月、日
years = features['year']
months = features['month']
days = features['day']
# datetime格式
dates = [str(int(year))+'-'+str(int(month))+'-'+str(int(day)) for year,month,day in zip(years,months,days)]
dates = [datetime.datetime.strptime(date,'%Y-%m-%d') for date in dates]
print(dates[:5])
运行结果
可以看到有348个样本和9个特征

前 5 个时间是连续递增的(如 1 月 1 日→1 月 2 日→…→1 月 5 日),可初步确认时间数据没有出现乱序,为后续时间序列分析(如按日期排序、时序建模)排除基础问题
绘图展示
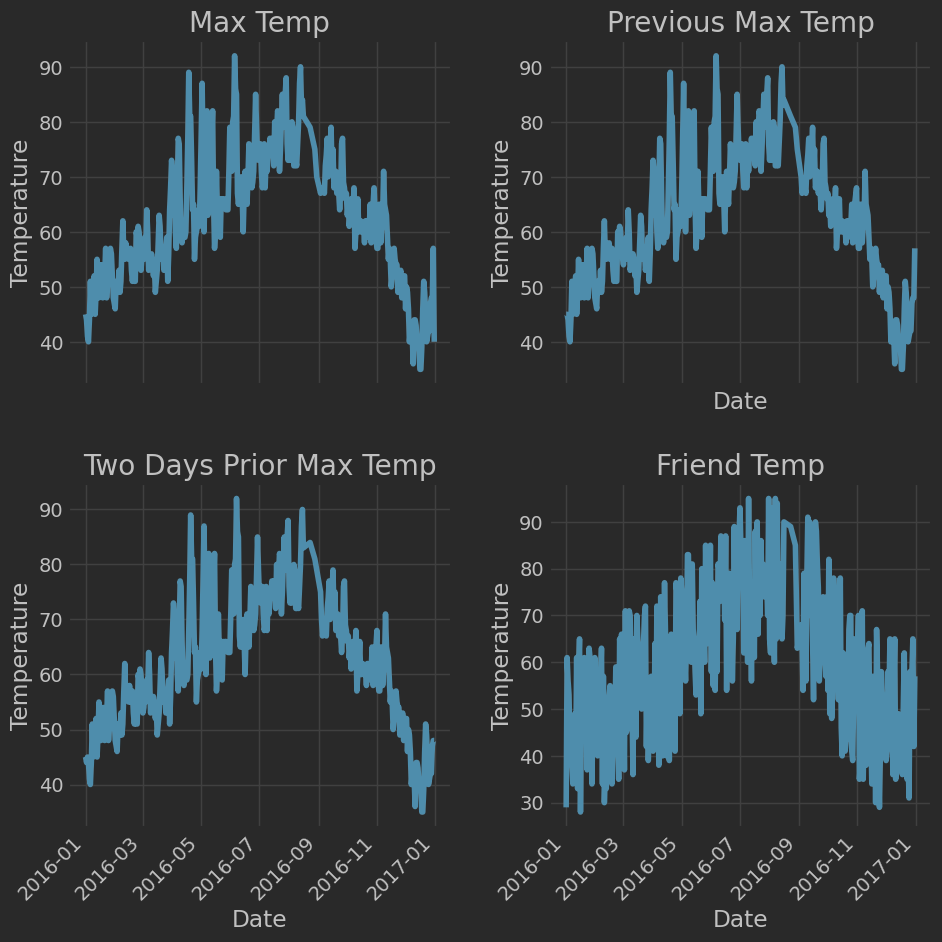
绘制实际最高温度、前一天最高温度、前两天最高温度和猜测最高温度随时间变化的图。
# 画图
plt.style.use('fivethirtyeight')
# 设置布局
fig,((ax1,ax2),(ax3,ax4)) = plt.subplots(nrows=2,ncols=2,figsize=(10,10))
fig.autofmt_xdate(rotation=45)
# 标签值
ax1.plot(dates,features['actual'])
ax1.set_xlabel('');ax1.set_ylabel('Temperature');ax1.set_title('Max Temp')
# 昨天
ax2.plot(dates,features['temp_1'])
ax2.set_xlabel('Date');ax2.set_ylabel('Temperature');ax2.set_title('Previous Max Temp')
# 前天
ax3.plot(dates,features['temp_2'])
ax3.set_xlabel('Date');ax3.set_ylabel('Temperature');ax3.set_title('Two Days Prior Max Temp');
# 猜测
ax4.plot(dates,features['friend'])
ax4.set_xlabel('Date');ax4.set_ylabel('Temperature');ax4.set_title('Friend Temp')
plt.tight_layout(pad=2)
效果展示
独热编码处理
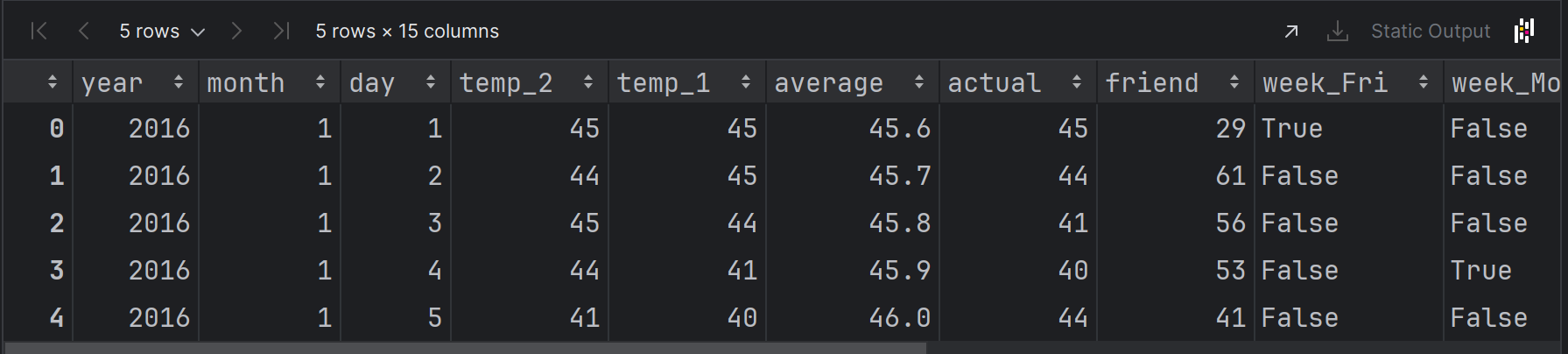
对features数据集中的分类变量进行 “独热编码” 处理,将非数值型的类别信息转换为机器学习模型可识别的数值格式。
# 独热编码
features = pd.get_dummies(features)
features.head(5)
运行结果
特征和标签处理
将数据集拆分为 “特征(输入)” 和 “标签(目标)”,并转换为模型可接受的数值格式,最后查看数据维度。
# 标签
labels = np.array(features['actual'])
# 在特征中去掉标签
features = features.drop('actual',axis=1)
# 单独保留名称
feature_list = list(features.columns)
# 转换成合适格式
features = np.array(features)
print(features.shape)
运行结果
处理后的数据中有348个样本和14个特征。

标准化处理
对输入特征进行 “标准化处理”,将所有特征调整到统一的数值范围(均值为 0、标准差为 1),避免因特征量级差异影响模型训练效果,这是机器学习特征工程中的关键步骤,最后查看标准化后的后的的输入特征矩阵 input_features 中第一个样本(索引为 0)的所有特征值,核心目的是验证标准化处理的结果是否符合预期。
from sklearn import preprocessing
input_features = preprocessing.StandardScaler().fit_transform(features)
input_features[0]
运行结果

基于Keras构建网络模型
使用 TensorFlow 的 Keras API 构建一个基础的全连接神经网络,用于后续的回归任务
一些常用参数如下:
- activation:激活函数的选择,一般常用relu
- kernel_initializer,bias_initializer:权重与偏置参数的初始化方法
- kernel_regularizer,bias_regularizer:加入正则化,
- inputs:输入,可以自己指定,也可以让网络自动选
- units:神经元个数
输入特征→ 16 神经元隐藏层 → 32 神经元隐藏层 → 1 神经元输出层
model = tf.keras.Sequential()
model.add(layers.Dense(16))
model.add(layers.Dense(32))
model.add(layers.Dense(1))
配置参数
配置神经网络模型的训练参数,明确模型在训练过程中如何优化权重(指定SGD(随机梯度下降)优化器)、如何衡量预测误差(指定损失函数(均方误差(MSE))),为后续的模型训练(model.fit())做准备。
model.compile(optimizer=tf.keras.optimizers.SGD(0.001), loss='mean_squared_error')
模型训练
启动神经网络模型的训练过程,通过输入特征和标签数据迭代更新模型权重,同时用部分数据验证模型泛化能力。
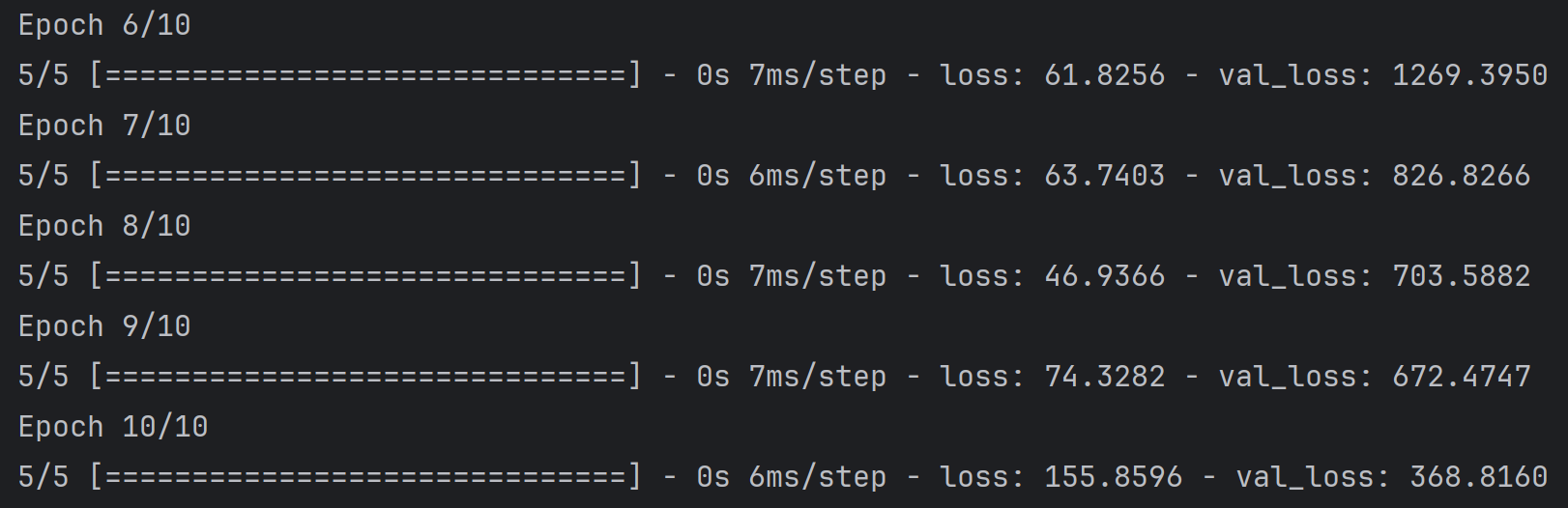
model.fit(input_features, labels, validation_split=0.25, epochs=10, batch_size=64)
训练展示
loss(训练集损失):在训练过程中波动较大(如 Epoch 6 损失 61.8,Epoch 9 升到 74.3,Epoch 10 又涨到 155.9),说明模型在训练集上的学习不稳定,没有形成稳定下降的学习趋势。
val_loss(验证集损失):始终远高于训练集损失(如 Epoch 6 训练损失 61.8,验证损失 1269.4;Epoch 10 训练损失 155.9,验证损失 368.8),且验证损失虽有下降但整体数值极大,这是过拟合且模型泛化能力差的典型表现
更改初始化方式
在之前基础神经网络结构的基础上,新增了权重初始化方式的指定配置,通过构建了一个指定用 “随机正态分布” 初始化全连接层权重的序列式神经网络。
model = tf.keras.Sequential()
model.add(layers.Dense(16,kernel_initializer='random_normal'))
model.add(layers.Dense(32,kernel_initializer='random_normal'))
model.add(layers.Dense(1,kernel_initializer='random_normal'))
模型编译、模型训练
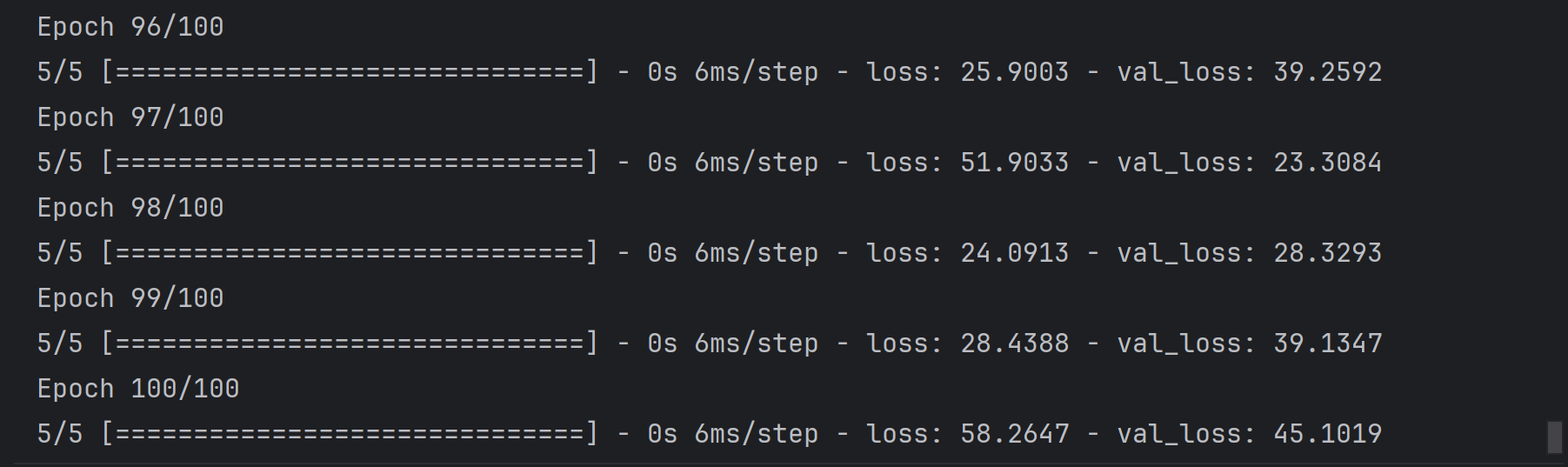
核心调整是将epochs从 10 增至 100,目的是让模型有更充足的迭代次数学习特征与温度的关联规律。
model.compile(optimizer=tf.keras.optimizers.SGD(0.001), loss='mean_squared_error')
model.fit(input_features, labels, validation_split=0.25, epochs=100, batch_size=64)
运行结果
新增L2正则化配置
在之前神经网络结构的基础上,新增了L2 正则化(权重衰减) 配置,通过限制权重的数值大小来缓解过拟合风险,构建了更稳健的回归模型。
model = tf.keras.Sequential()
model.add(layers.Dense(16,kernel_initializer='random_normal',kernel_regularizer=tf.keras.regularizers.l2(0.03)))
model.add(layers.Dense(32,kernel_initializer='random_normal',kernel_regularizer=tf.keras.regularizers.l2(0.03)))
model.add(layers.Dense(1,kernel_initializer='random_normal',kernel_regularizer=tf.keras.regularizers.l2(0.03)))
模型编译、模型训练
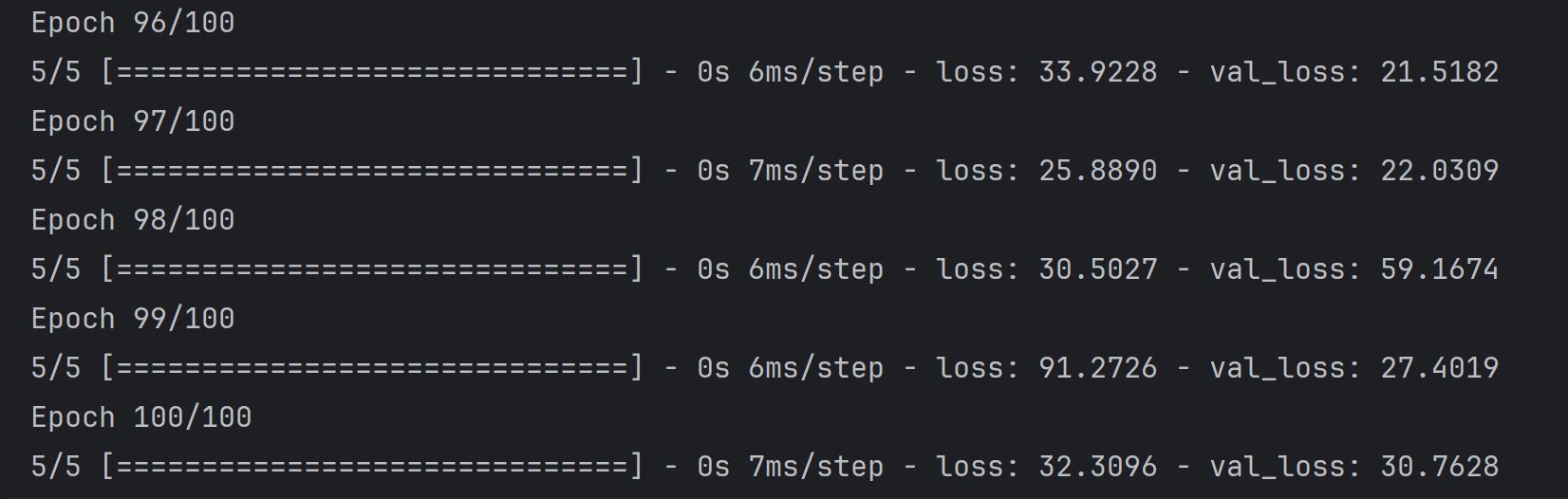
模型编译中配置带正则化适配的训练规则并在训练时通过100 轮迭代强化正则化效果。
model.compile(optimizer=tf.keras.optimizers.SGD(0.001), loss='mean_squared_error')
model.fit(input_features, labels, validation_split=0.25, epochs=100, batch_size=64)
运行结果
可以看到训练集损失和验证集损失都降到了一个可观的效果
预测模型结果
使用训练完成的神经网络模型,对输入特征 input_features 进行预测,生成与样本数量对应的预测结果
predict = model.predict(input_features)
运行结果

测试结果展示
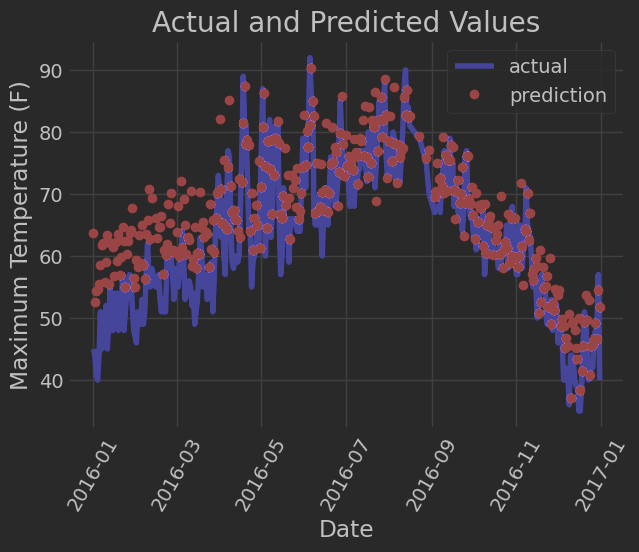
将 “日期、真实标签、模型预测值” 三者关联,整理成结构化的 DataFrame 表格,方便后续通过日期对齐来分析模型预测效果,并通过 matplotlib 绘制时间序列图表,直观对比 “真实温度值” 与 “模型预测温度值” 的差异,清晰展示模型在不同日期的预测效果
# 转换日期格式
dates = [str(int(year)) + '-' + str(int(month)) + '-' + str(int(day)) for year, month, day in zip(years, months, days)]
dates = [datetime.datetime.strptime(date, '%Y-%m-%d') for date in dates]# 创建一个表格来存日期和其对应的标签数值
true_data = pd.DataFrame(data = {'date': dates, 'actual': labels})# 同理,再创建一个来存日期和其对应的模型预测值
months = features[:, feature_list.index('month')]
days = features[:, feature_list.index('day')]
years = features[:, feature_list.index('year')]test_dates = [str(int(year)) + '-' + str(int(month)) + '-' + str(int(day)) for year, month, day in zip(years, months, days)]test_dates = [datetime.datetime.strptime(date, '%Y-%m-%d') for date in test_dates]predictions_data = pd.DataFrame(data = {'date': test_dates, 'prediction': predict.reshape(-1)})
# 真实值
plt.plot(true_data['date'], true_data['actual'], 'b-', label = 'actual')# 预测值
plt.plot(predictions_data['date'], predictions_data['prediction'], 'ro', label = 'prediction')
plt.xticks(rotation = 60)
plt.legend()# 图名
plt.xlabel('Date'); plt.ylabel('Maximum Temperature (F)'); plt.title('Actual and Predicted Values');
效果展示
可以看到大部分红色散点与蓝色线条的 “垂直距离” 较小,说明多数日期的预测值与真实值偏差不大,模型在常规日期的预测精度较好。