机器人中的李代数是什么

目的

　　很多机器人的初学者在第一次接触到李群和李代数时通常会感到困惑，它们到底有什么物理意义？有没有通俗易懂的、直观的解释。本文尝试从几个角度对李代数进行解读。

1　“角速度”解释

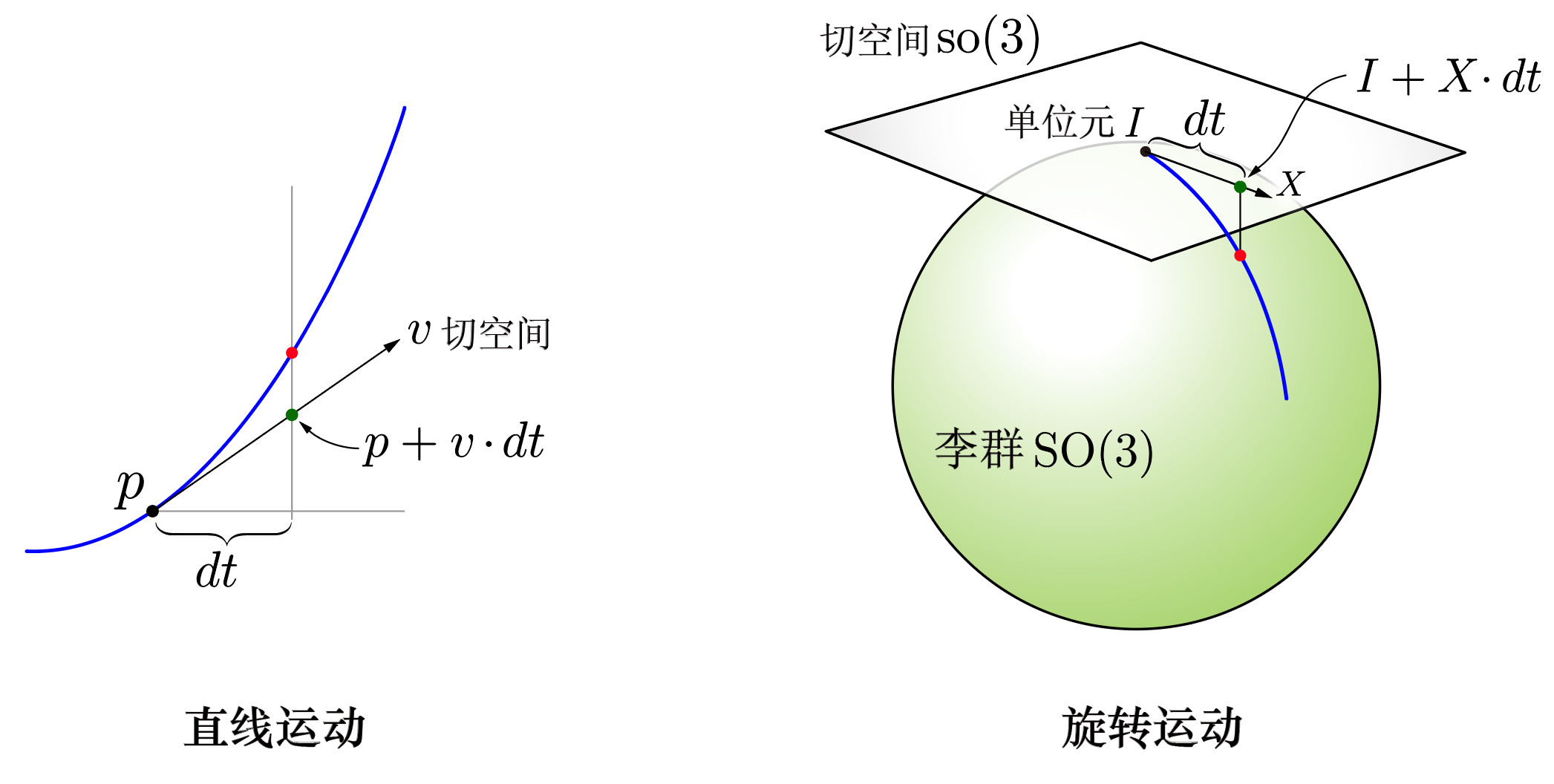
　　我们先考虑简单的直线运动。已知一个物体在当前时刻的位置是 $p$ ，而速度是 $v$。如果我们想知道经过一个很小的时间间隔 $dt$ 之后物体到达的位置，应该如何计算呢？我们可以用当前时刻的速度进行估计，$dt$ 之后物体到达的位置（我们用$p^{\prime }$表示）是：
$$\begin{array}{r}{p}^{\prime }=p+v\cdot dt\end{array}\text{\hspace{1em}(1)}$$

　　现在考虑物体做旋转运动。同样的，已知物体在当前时刻的姿态是 $I$ ，而旋转速度是 $X$。如果我们想知道经过一个很小的时间间隔 $dt$ 之后物体的姿态，应该如何计算呢？思路是一样的，我们利用当前时刻的旋转速度进行估计（我们用$R^{\prime }$表示），计算方式如下式。

$$\begin{array}{r}{R}^{\prime }=I+X\cdot dt\end{array}\text{\hspace{1em}(2)}$$

　　在数学中，一般用大写字母表示矩阵，小写字母表示矢量。位置是一个矢量，所以一般用小写字母来表示（例如前面的$p$）。在机器人领域，通常用一个被称为旋转矩阵的东西表示物体的姿态，所以用大写字母表示物体的姿态（例如前面的$I$和$R^{\prime }$）。
　　这个旋转速度$X$就是一个李代数，它也是一个矩阵。
　　李代数经常被描述为李群的切空间，这是为什么呢？通过上面的例子就容易猜到了。物体在做直线运动时，速度就是位置曲线的切线斜率，这个切线所在的空间就是位置的切空间。旋转运动类似，旋转速度也位于切空间。由于李群$SO(3)$是一个四维空间中的三维弯曲球面，我们无法在三维空间中展示出来，因此这里使用三维空间中的二维弯曲球面进行示意。

2　“无穷小旋转矩阵”解释

　　李群的创立者索菲斯·李为了研究无穷小变换发明了李代数这个概念，所以李代数就是无穷小旋转矩阵。对于一个很小的李代数$X$，我们想用它构造一个很小的旋转$R$，可以这样做（$I$是个单位矩阵）：

$$\begin{array}{r}R=I+X\end{array}\text{\hspace{1em}(3)}$$

　　在使用旋转矩阵的时候，我们很少看到矩阵之间的加法。旋转矩阵之间不能相加，因为没有意义。但是这里确实可以，因为这里李代数是个无穷小量。而无穷小量的计算似乎遵守另一套逻辑。暂时不管这么多了，往下算就是了。
　　举个具体的例子，对于很小的李代数$X$

$$\begin{array}{r}X=\left[\begin{array}{ccc}0& -0.03& 0.02\\ 0.03& 0& -0.01\\ -0.02& 0.01& 0\end{array}\right]\end{array}\text{\hspace{1em}(4)}$$
　　我们计算乘积$R{R}^{\text{T}}$，结果如下。可以发现，乘积$R{R}^{\text{T}}$很接近单位矩阵。所以，$R$确实可以近似看成是一个旋转矩阵。

$$\begin{array}{rl}& R{R}^{\mathrm{T}}\\ =& (I+X)(I+X{)}^{\mathrm{T}}\\ =& \left[\begin{array}{ccc}1& -0.03& 0.02\\ 0.03& 1& -0.01\\ -0.02& 0.01& 1\end{array}\right]\cdot {\left[\begin{array}{ccc}1& -0.03& 0.02\\ 0.03& 1& -0.01\\ -0.02& 0.01& 1\end{array}\right]}^{\text{T}}\\ =& \left[\begin{array}{ccc}1.0013& -0.0002& -0.0003\\ -0.0002& 1.001& -0.0006\\ -0.0003& -0.0006& 1.0005\end{array}\right]\\ \approx & \left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right]\end{array}\text{\hspace{1em}(5)}$$

　　我们说“近似”是，那什么时候才真正是呢？这就要用到指数映射了。假如我们再加一项，用$I+X+\frac{X^2}{2}$表示$R$，会发现得到结果比上面的更接近单位矩阵 $I$ 了。所以下面有请好朋友——指数映射登场。

$$\begin{array}{rl}& R{R}^{\mathrm{T}}\\ =& \left(I+X+\frac{X^2}{2}\right){\left(I+X+\frac{X^2}{2}\right)}^{\mathrm{T}}\\ =& \left[\begin{array}{ccc}1& 0.00000007& 0.000000105\\ 0.00000007& 1& 0.00000021\\ 0.000000105& 0.00000021& 1\end{array}\right]\end{array}\text{\hspace{1em}(6)}$$

　　指数映射就是指数函数$e^x$，其中的$x$就是个实数。如果把实数$x$换成一个矩阵也是有意义的，为了便于区分就叫$e^X$指数映射了。学过一点高等数学的同学可能还记得，指数函数有两种定义方法：
　　$(1)$　一种是无穷级数：

$$e^x=1+\frac{x}{1!}+\frac{x^2}{2!}+\frac{x^3}{3!}+\frac{x^4}{4!}+\cdots \text{\hspace{1em}(7)}$$

　　$(2)$　另一种是二项式的极限：

$$e^x=\underset{n\to \infty }{\lim }{\left(1+\frac{x}{n}\right)}^n\text{\hspace{1em}(8)}$$

　　这两种方式都可以逼近指数函数，但是级数形式更快（实际上级数形式比极限形式要快得多）。下图左侧是级数形式，右侧是极限形式。红色点表示指数函数上实际的点，蓝色的点是取有限项计算得到的近似点。

　　 　

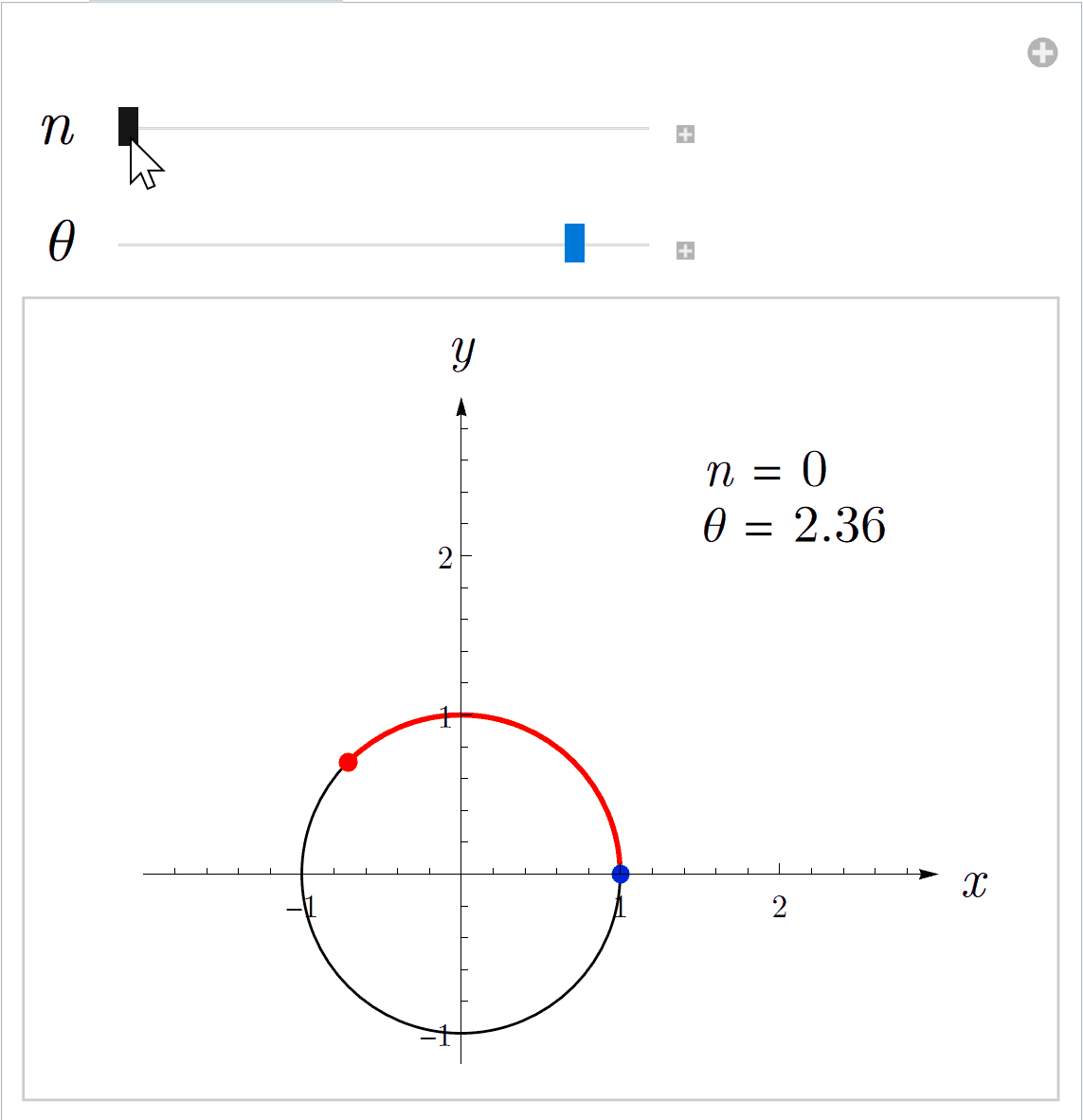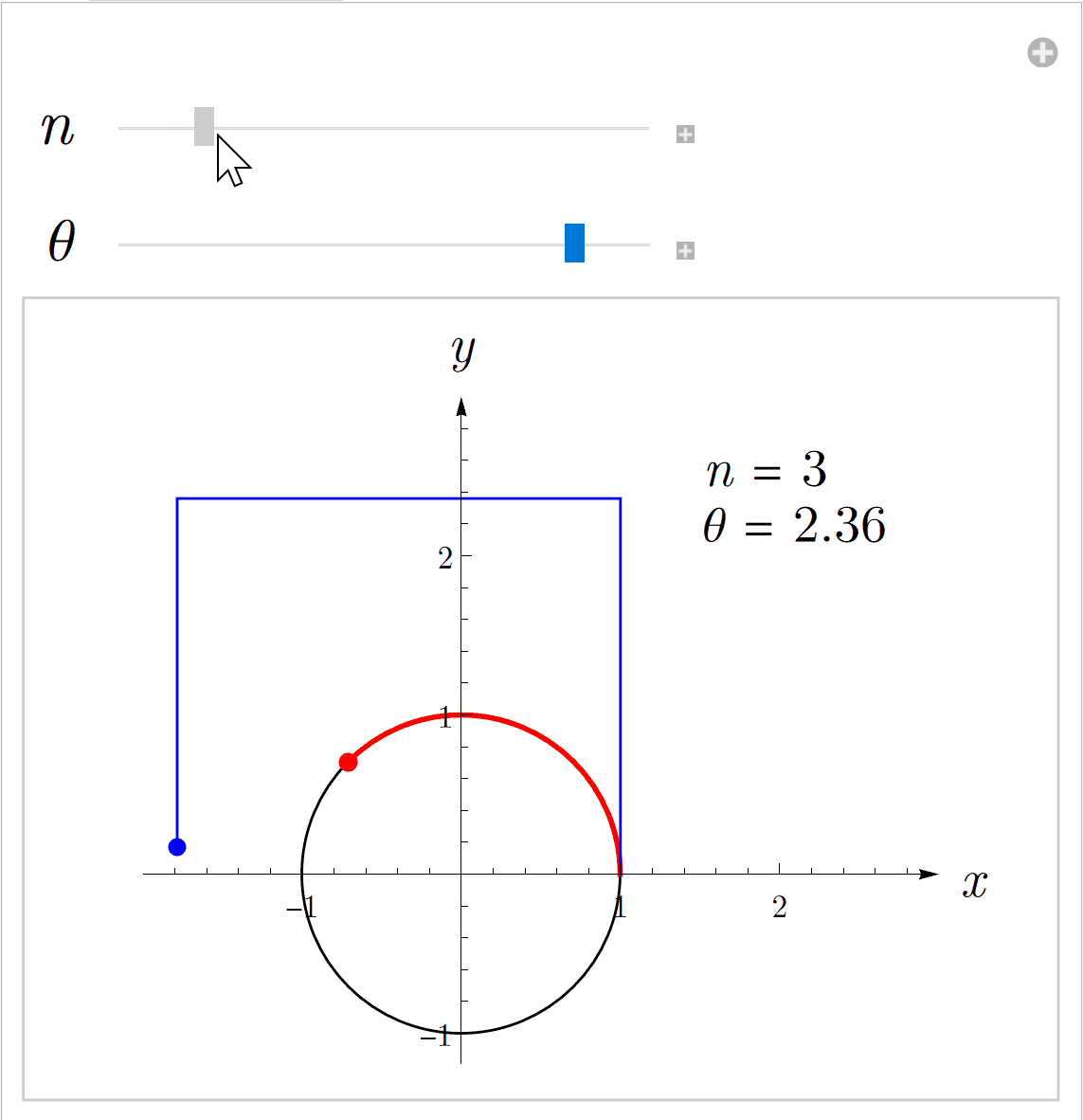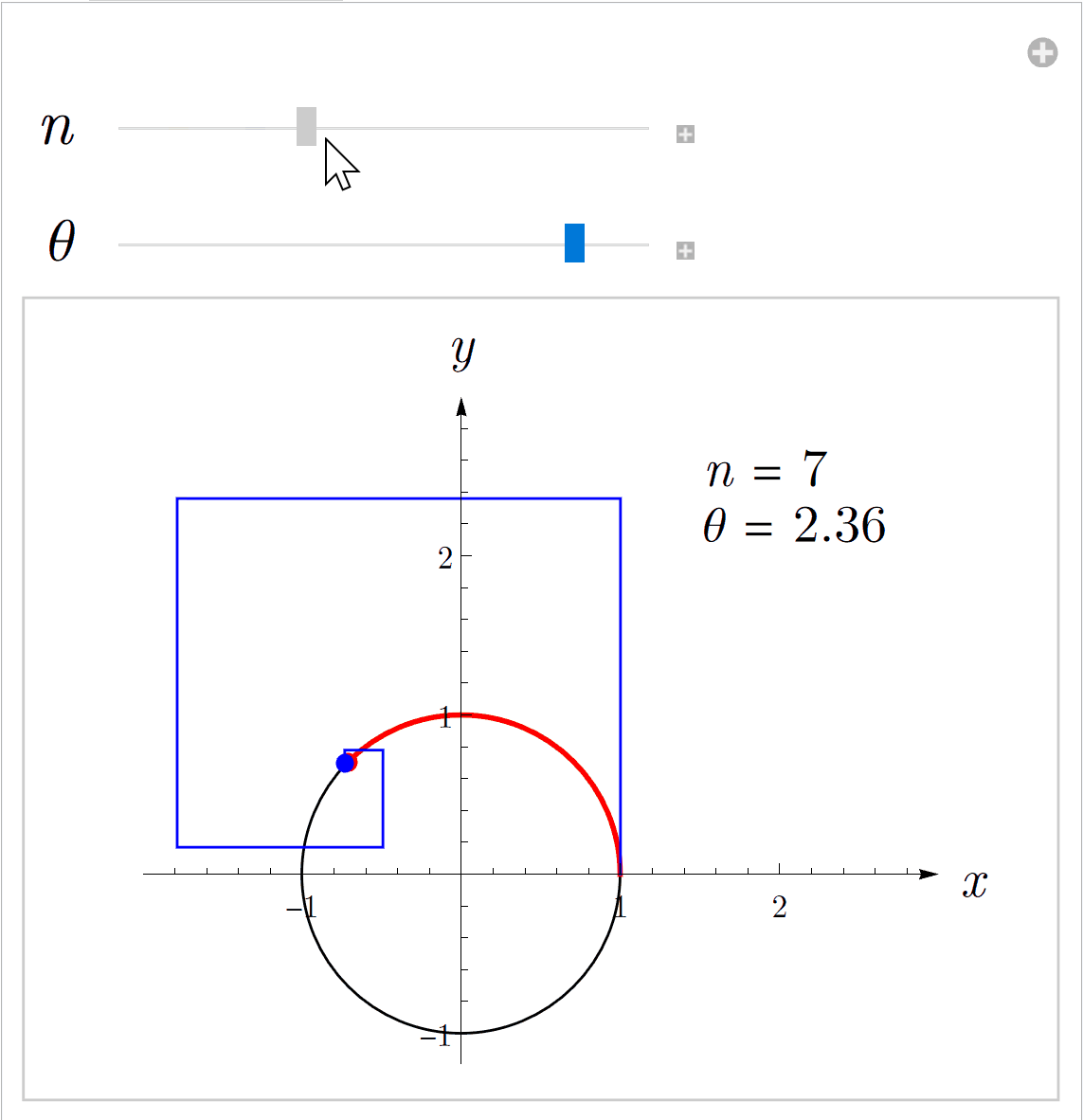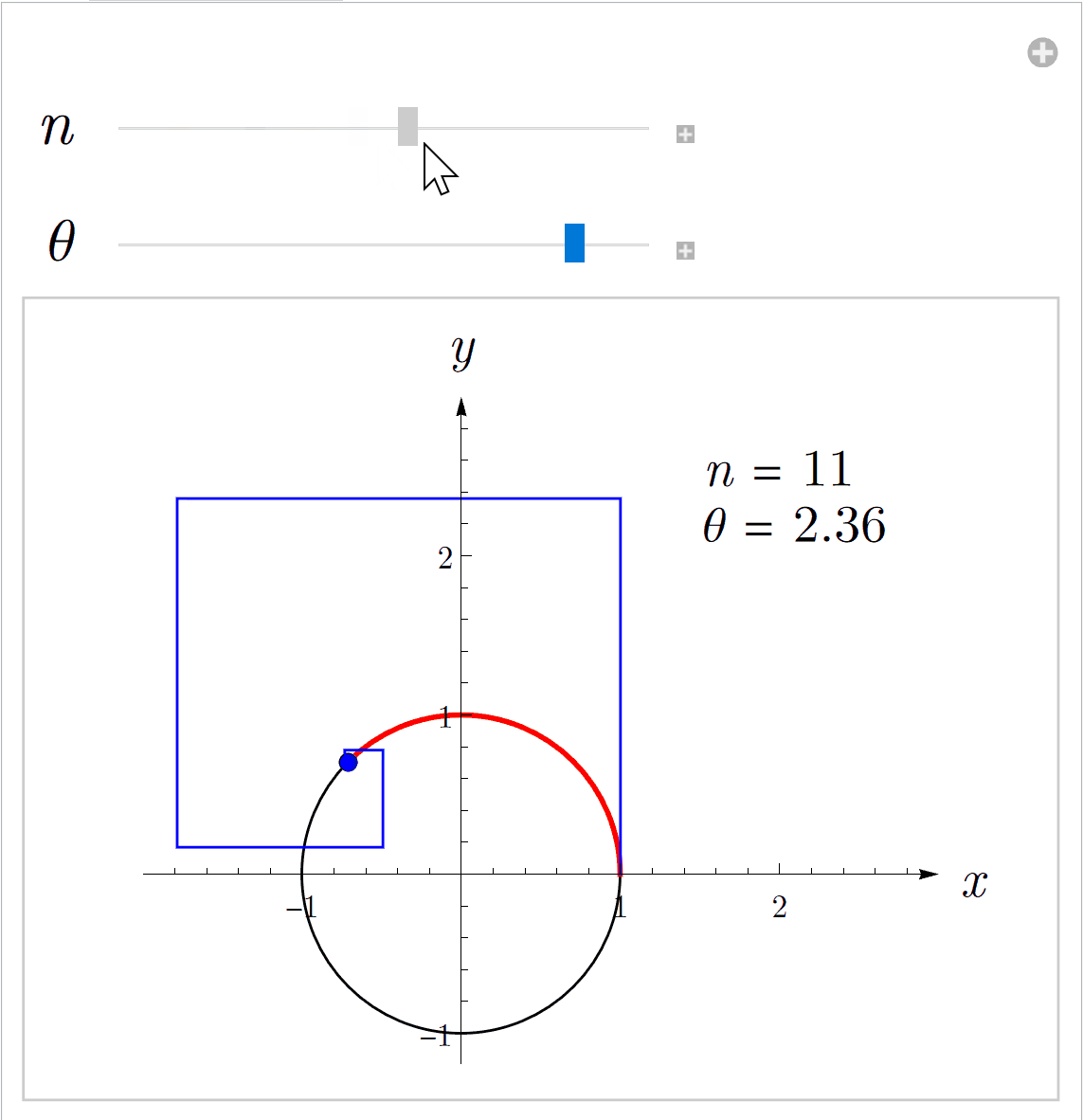
　　欧拉发现，如果把实数扩展到复数，也就是把复数带入指数函数的定义，可以得到下面的公式$(9)$，这就是大名鼎鼎的欧拉公式。上面的动画就是将$i\theta$带入指数函数的定义式后，把结果的实部和虚部分别作为$(x,y)$坐标画在坐标系中的图像。其中，$n$表示级数或者二项式中的项数，$\theta$是一个实数。

$$e^{i\theta }=\cos (\theta )+i\sin (\theta )\text{\hspace{1em}(9)}$$

3　“轴-角度”解释

　　可以看到，欧拉公式描述了二维平面中的旋转。那么三维空间如何表示旋转呢？可能是受到欧拉公式的启发，一个名为罗德里格斯的年轻人得到了三维旋转的表达形式$(10)$，这个公式没有欧拉公式那么家喻户晓，但是搞不好可能会偶尔用到，它被称为罗德里格斯公式。罗德里格斯公式的推导过程非常有趣，可以参考相关文献。将李代数$X$写成向量的形式，$X=\theta \hat{u}$，其中$u$是一个单位向量，$\theta$是李代数向量的“长度”（范数）。

$$\begin{array}{rl}& e^X\\ =& \sum _{n=0}^{\infty }\frac{(\theta \hat{u}{)}^n}{n!}\\ =& I+\frac{\theta \hat{u}}{1!}+\frac{{\theta }^2{\hat{u}}^2}{2!}+\frac{{\theta }^3{\hat{u}}^3}{3!}+\frac{{\theta }^4{\hat{u}}^4}{4!}+\frac{{\theta }^5{\hat{u}}^5}{5!}+\cdots \\ =& (u{u}^{\mathrm{T}}-\hat{u}\hat{u})+\theta \hat{u}+\frac{1}{2!}{\theta }^2{\hat{u}}^2+\frac{1}{3!}{\theta }^3(-\hat{u})+\frac{1}{4!}{\theta }^4(-\hat{u}\hat{u})+\frac{1}{5!}{\theta }^5\hat{u}+\cdots \\ =& u{u}^{\mathrm{T}}+\underset{\sin (\theta )}{\underbrace{\left(\theta -\frac{1}{3!}{\theta }^3+\frac{1}{5!}{\theta }^5-\cdots \right)}}\hat{u}-\underset{\cos (\theta )}{\underbrace{\left(1-\frac{1}{2!}{\theta }^2+\frac{1}{4!}{\theta }^4-\cdots \right)}}\hat{u}\hat{u}\\ =& (\hat{u}\hat{u}+I)+\sin (\theta )\hat{u}-\cos (\theta )\hat{u}\hat{u}\\ =& I+\sin (\theta )\hat{u}+(1-\cos (\theta ))\hat{u}\hat{u}\end{array}\text{\hspace{1em}(10)}$$

　　向量$u$可以视为旋转轴，$\theta$是绕这根轴旋转的角度，所以李代数是不是可以视为绕某根轴旋转一个角度呢？
　　李代数$X$作用到向量的结果可以用叉积表示，例如我们将$X$记为：

$$X=\left[\begin{array}{ccc}0& -z& y\\ z& 0& -x\\ -y& x& 0\end{array}\right]\text{\hspace{1em}(11)}$$

　　那么，将李代数$X$作用到一个三维向量$v=(a,b,c)$（也就是矩阵向量相乘）将得到：

$$Xv=\left[\begin{array}{ccc}0& -z& y\\ z& 0& -x\\ -y& x& 0\end{array}\right]\cdot \left[\begin{array}{c}a\\ b\\ c\end{array}\right]=\left[\begin{array}{c}cy-bz\\ az-cx\\ bx-ay\end{array}\right]\text{\hspace{1em}(12)}$$

　　而两个三维向量的叉积定义如下式$(13)$，可以看到$(12)$与$(13)$完全相同。

$$(x,y,z)\times (a,b,c)=(cy-bz,az-cx,bx-ay)\text{\hspace{1em}(13)}$$

　　两个三维向量做叉积的结果也是一个三维向量，这个向量与前两个向量都垂直。我们可以想象，如果把一个李代数作用到空间中的每一个点，都可以得到一个新的向量，也就是说这个李代数生成了一个向量场。假如我们把这个向量场画出来会是什么样的呢？下图中的蓝色小箭头所示的就是李代数产生的向量场，当然我们不可能真的把每个点处的向量都画出来，这样太密集了，只能画出一些向量进行示意。如果我们改变李代数（对应向量的大小、方向），相应的所生成的向量场也会发生变化。由于生成的向量场中的向量总是与李代数（对应的向量）垂直，所以看上去这个向量场就是在围绕李代数旋转，李代数自然就是那个旋转轴。当然，旋转轴只需要单位向量就能确定，那向量的长度表示什么呢？向量的长度表示了旋转的程度（即旋转角度）。

　　旋转轴这个解释可比什么无穷小旋转矩阵、切空间那些解释直观多了。沿着这个方向思考，我们是否可以用李代数干点什么呢，比如插值？

　　给定两个位置点，我们可以在二者中间连一条线段，这条线段上的点就是二者之间的一系列点。那么对于旋转来说，给定任意两个姿态，如何表示它们之间的一系列姿态或者旋转呢？
　　一种思路是：
　　$(1)$ 计算差值旋转矩阵：假设从$R_1$经过旋转$∆R$到达$R_2$，如图所示。$∆R$可以由$R_1$和$R_2$得到：$∆R=R_1^{-1}{R}_2$。
　　$(2)$ 计算旋转轴和旋转角：旋转$∆R\in SO(3)$对应的旋转轴和旋转角可以由其李代数得到。我们知道从李代数得到李群可以借助指数映射。反之，从李群得到李代数需要使用对数映射（Logarithmic Map），即矩阵指数映射的逆运算。使用对数映射，我们可以将旋转矩阵变换为李代数空间中的元素（当然也就是个李代数了），即$log:e^X\to X$。将李代数的向量表示记为$\theta u$。其中，单位向量$u$表示从$R_1$到$R_2$的旋转轴。而实数$\theta$表示从$R_1$到$R_2$旋转的角度。
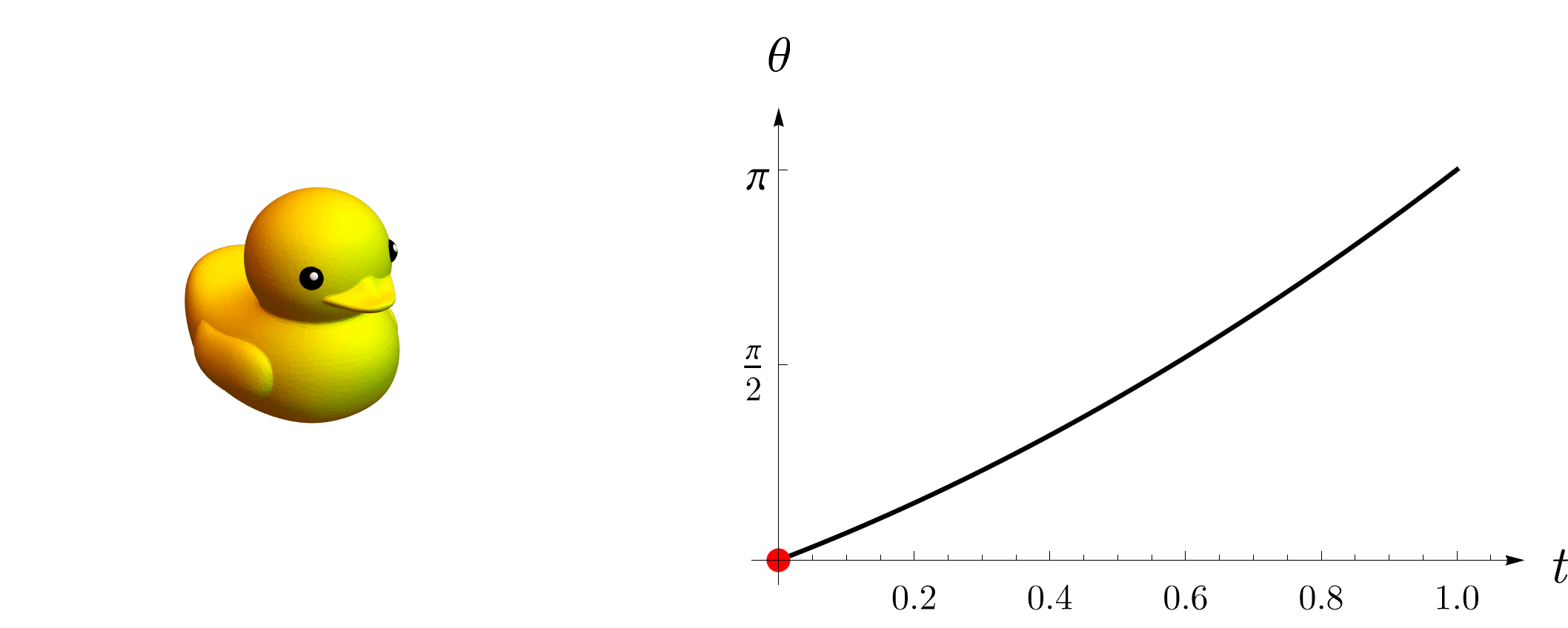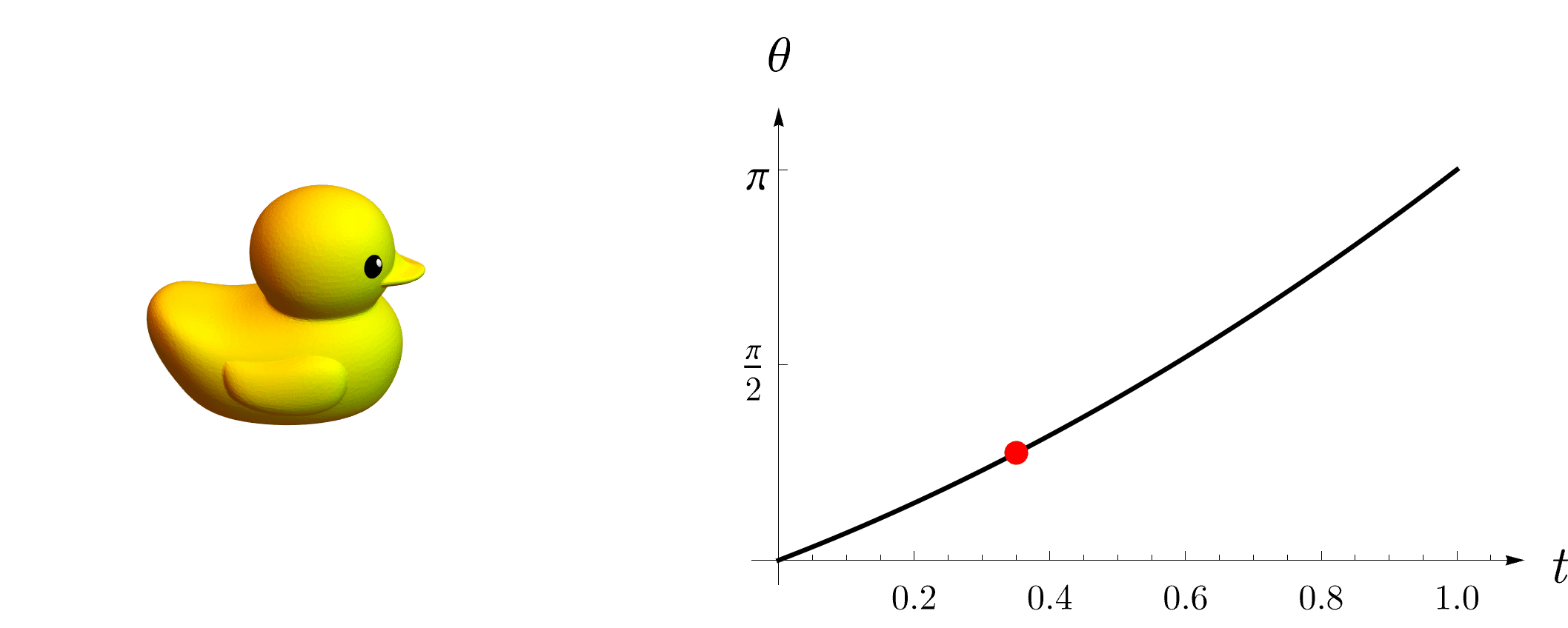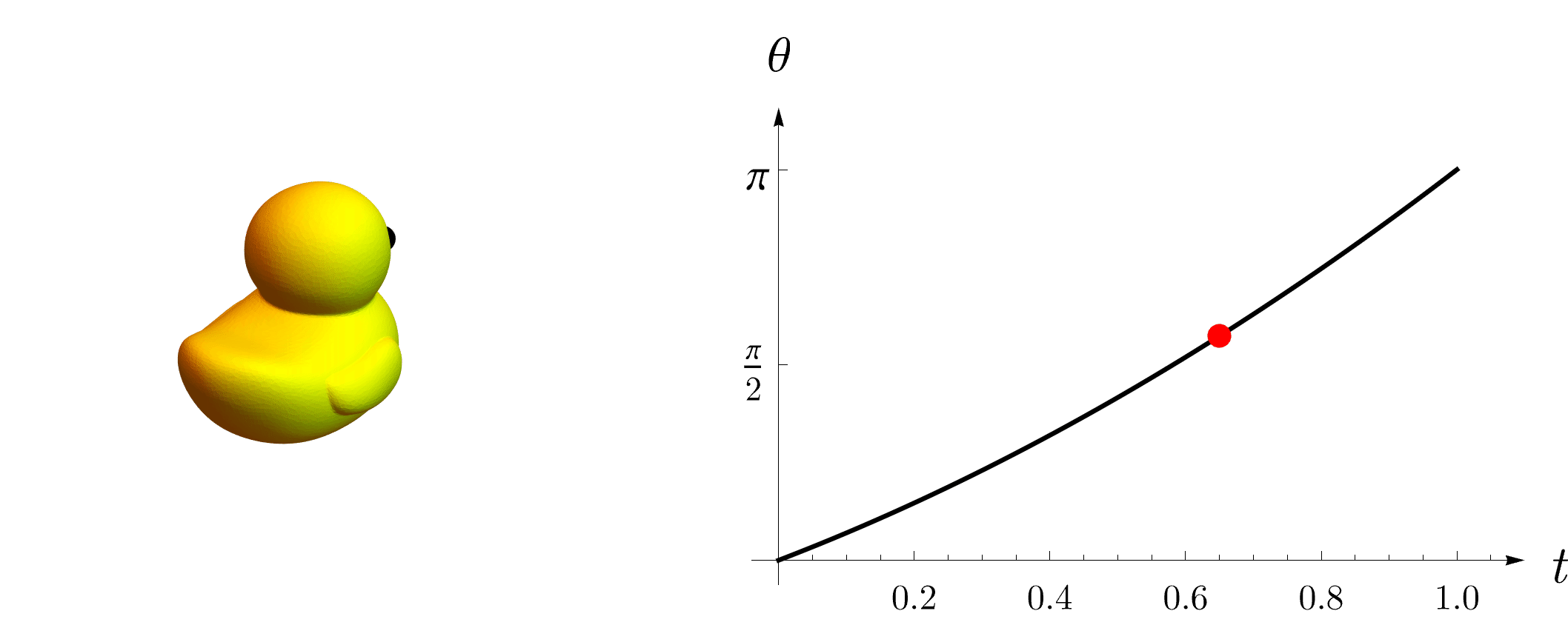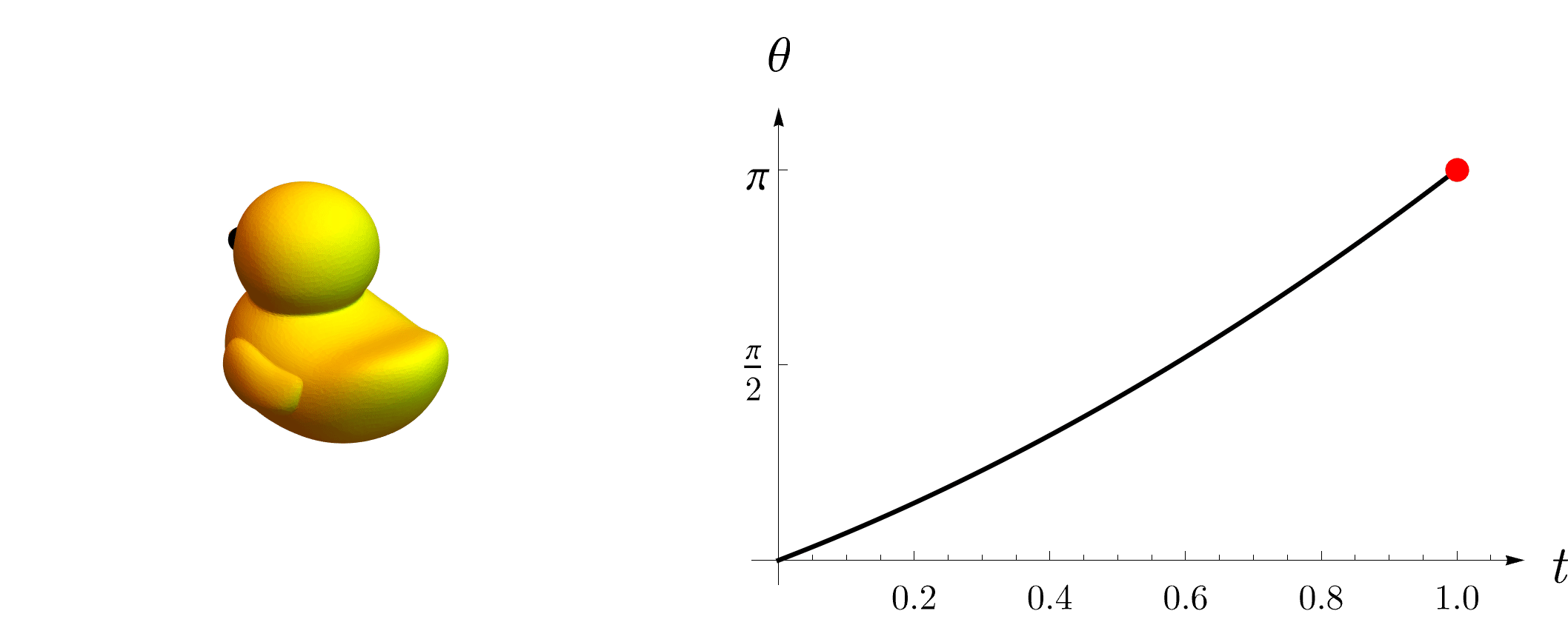
　　$(3)$ 改变旋转角：使用指数映射，我们只需要让角度从$0$变化到$\theta$即可得到一系列的中间旋转（期间并不改变旋转轴的朝向），如下图所示。
$$R_t=e^{t\hat{u}},t\in (0,\theta )$$

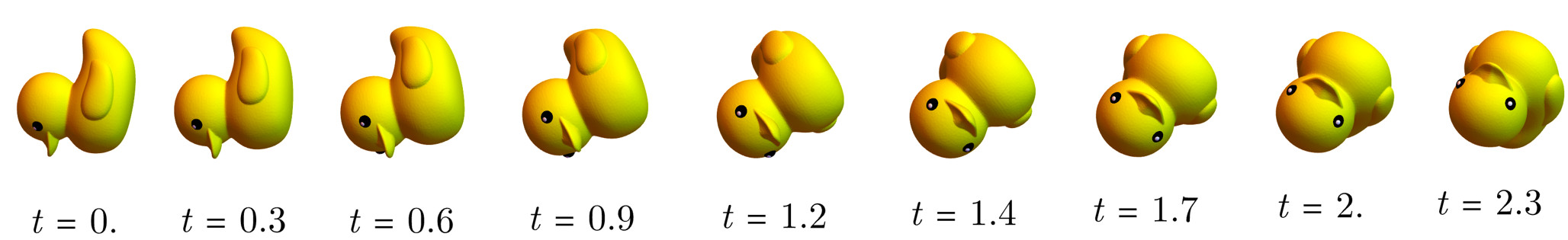
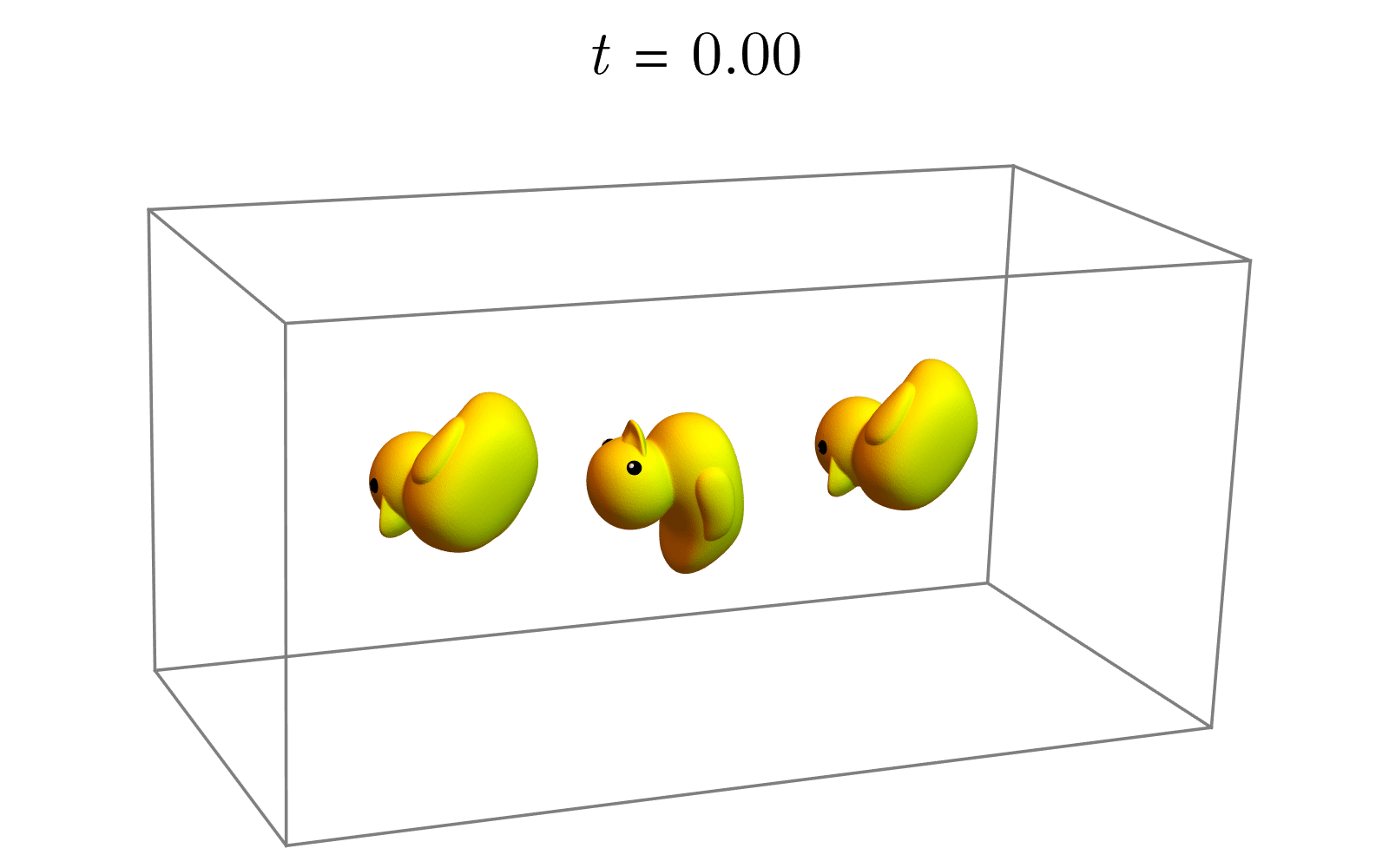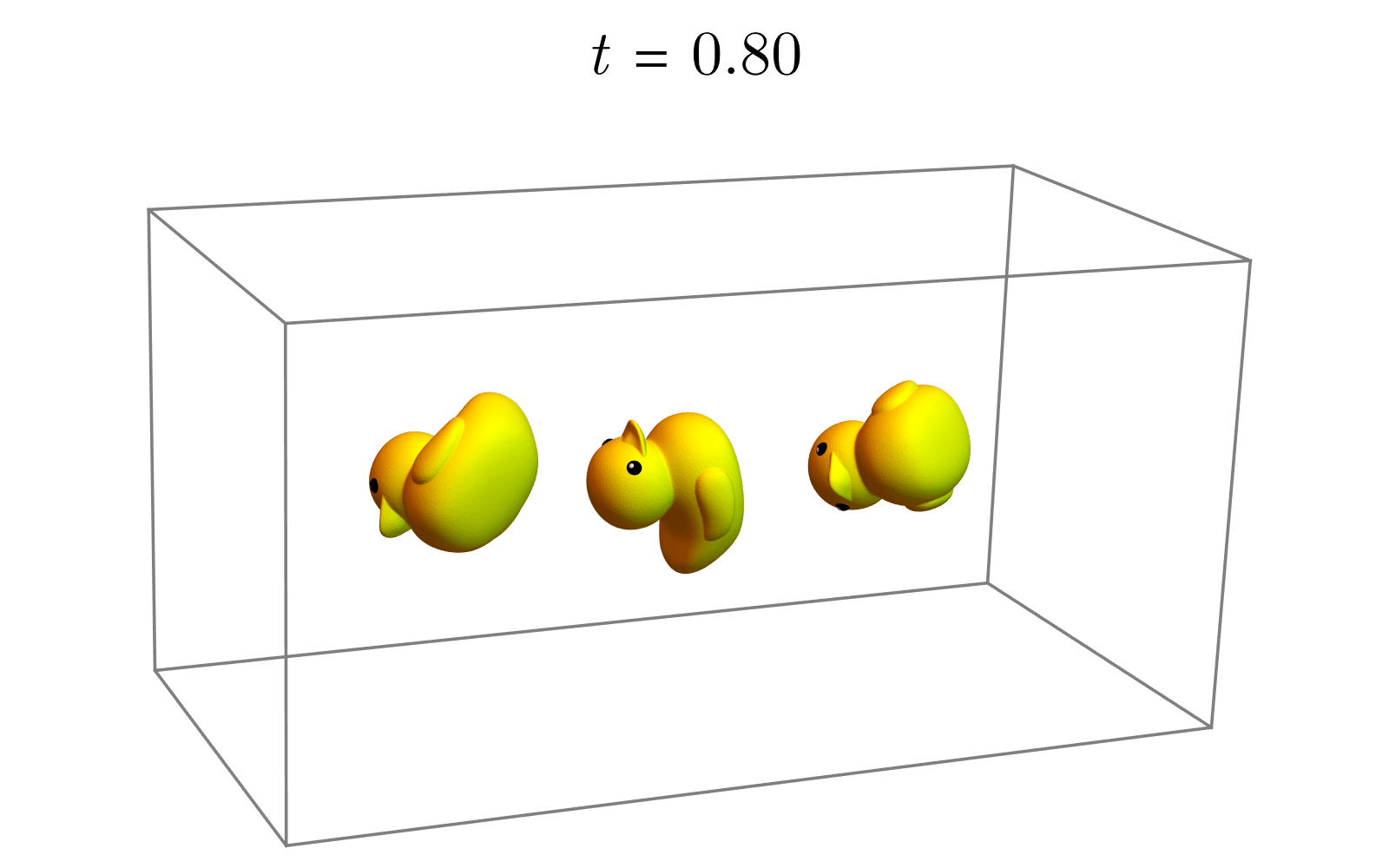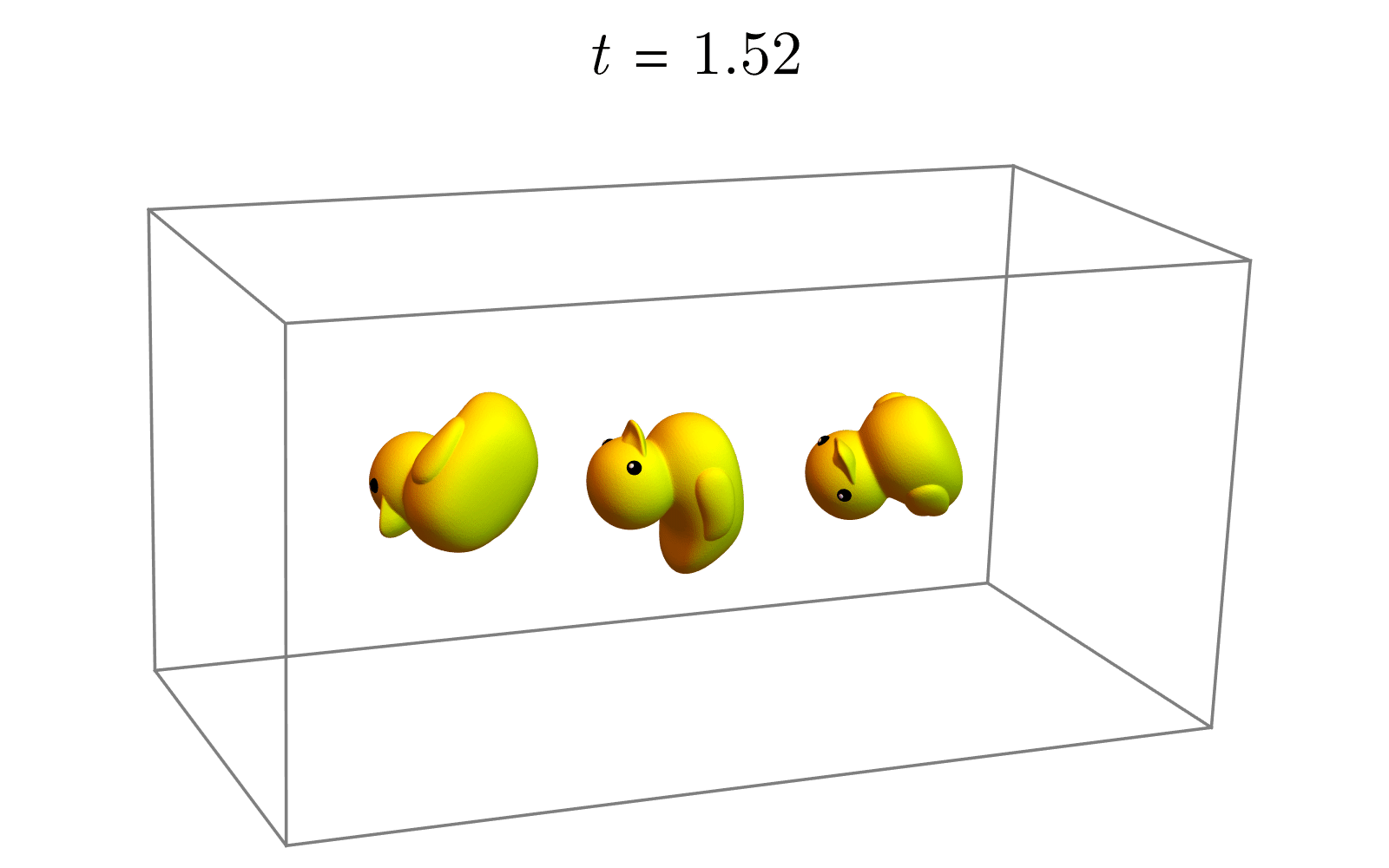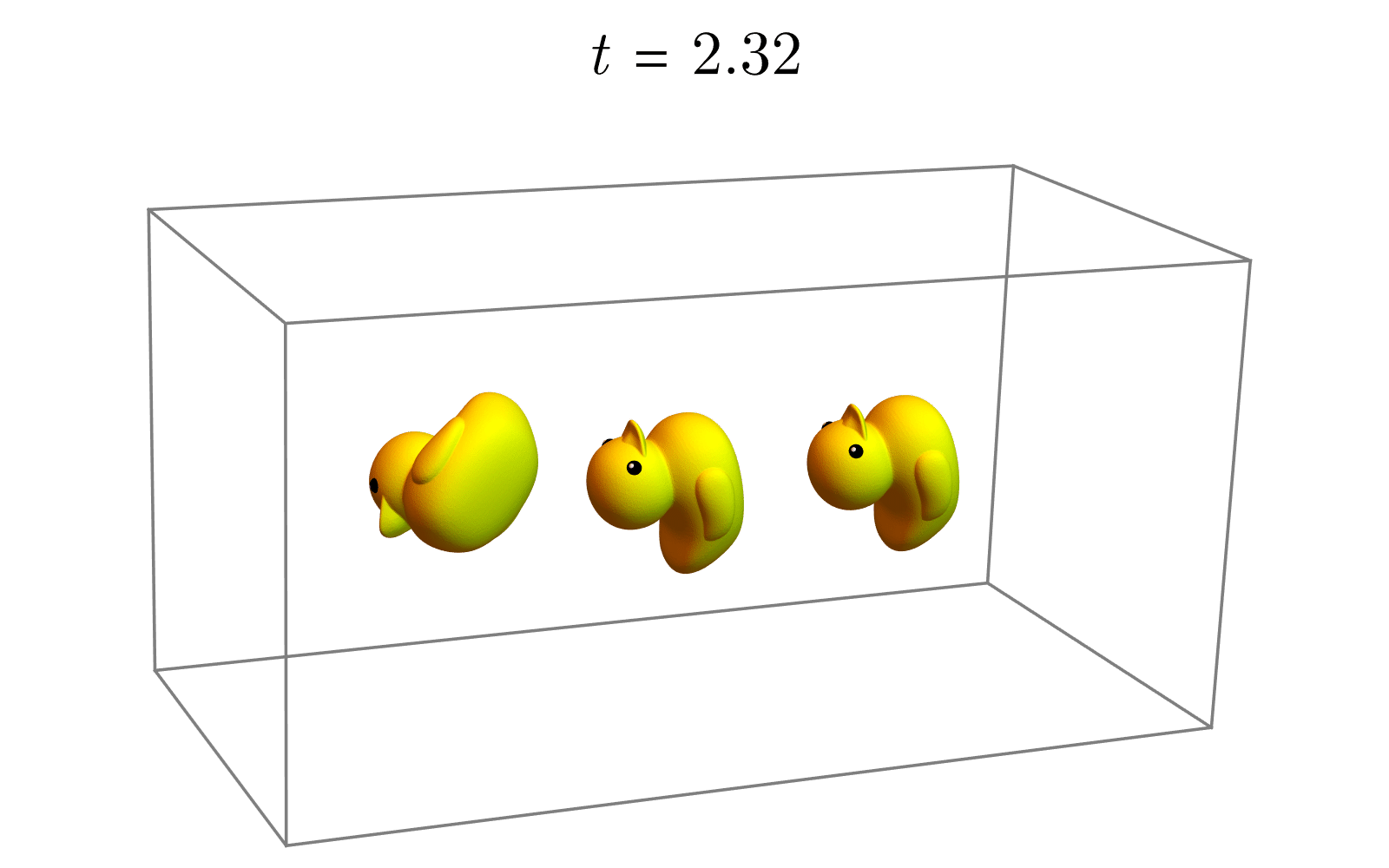
　　除了以上插值方法外，还有一种更简单、直接的方法，步骤如下。
　　$(1)$ 转换为李代数：我们可以将每个旋转矩阵$R_1$、$R_2$都视为李代数的指数映射。反过来，从旋转矩阵$R$也可以得到李代数，即：
$$\begin{gathered} X_1=log(R_1) \\ {X}_2=log(R_2) \end{gathered}$$

　　$(2)$ 线性插值：既然李代数是一个线性空间，我们就在李代数这个线性空间中进行线性插值，再借助指数映射将中间结果（李代数）转换为李群中的旋转：
$$R_t=e^{(1-t)X_1+t{X}_2},t\in (0,1)$$

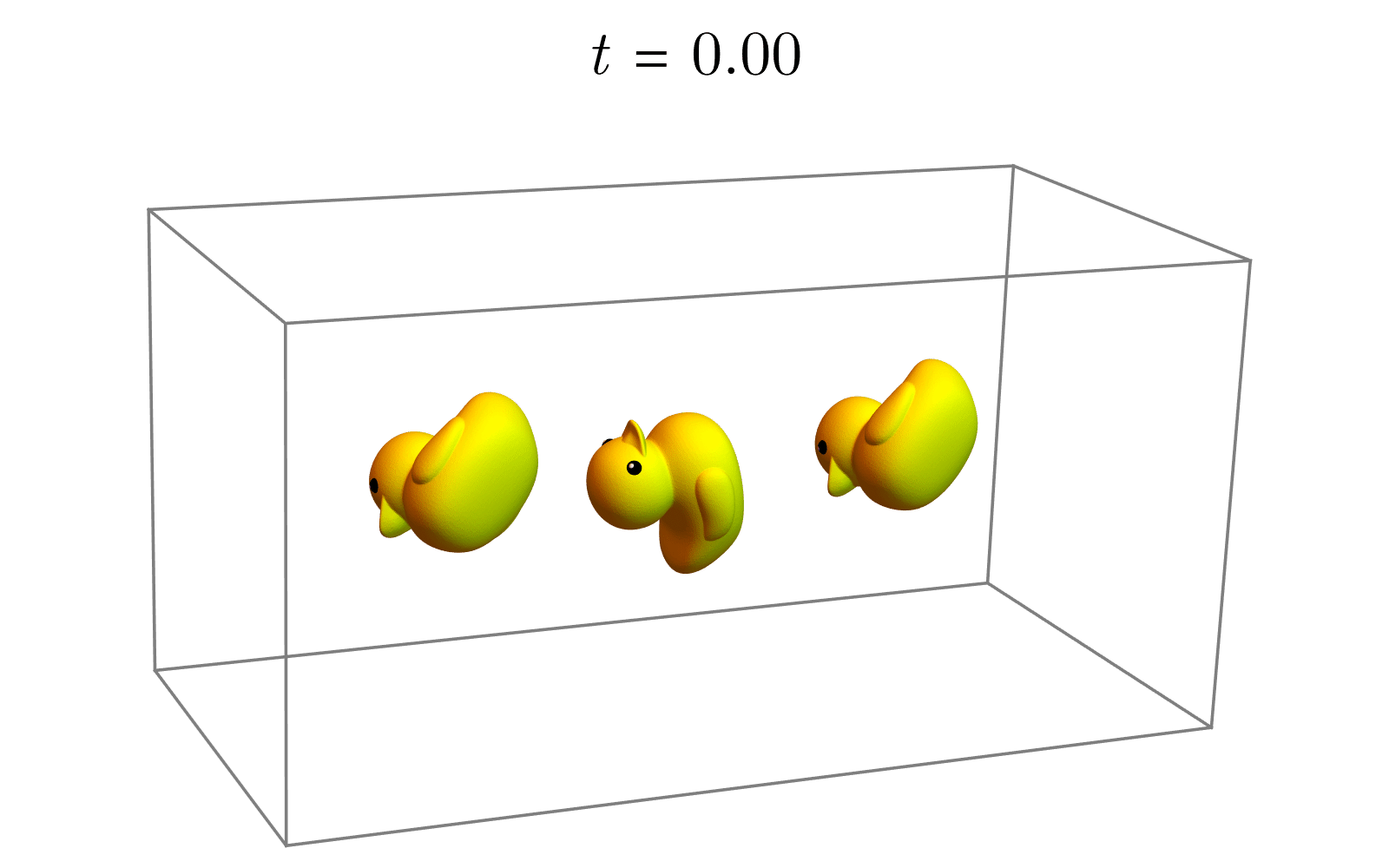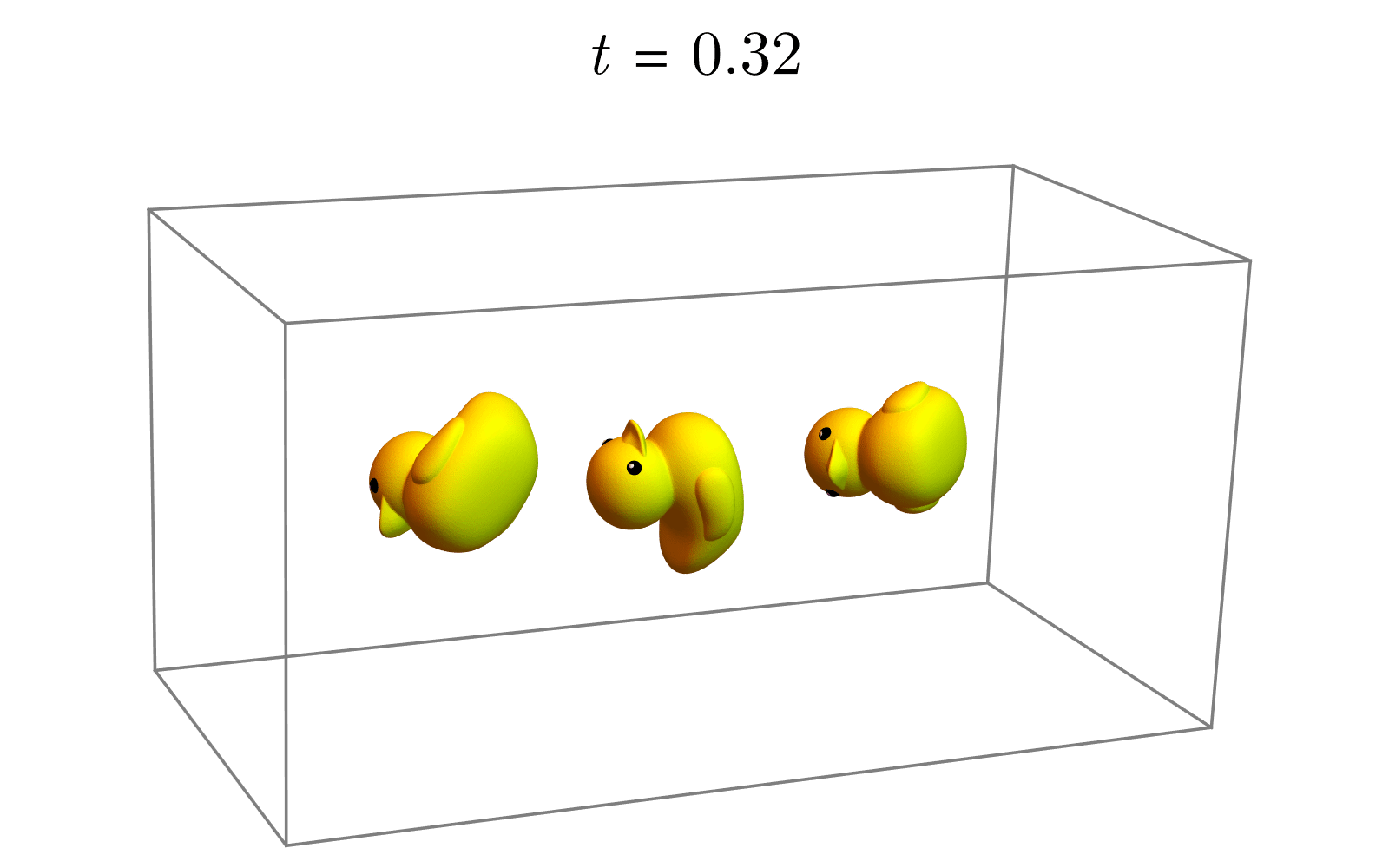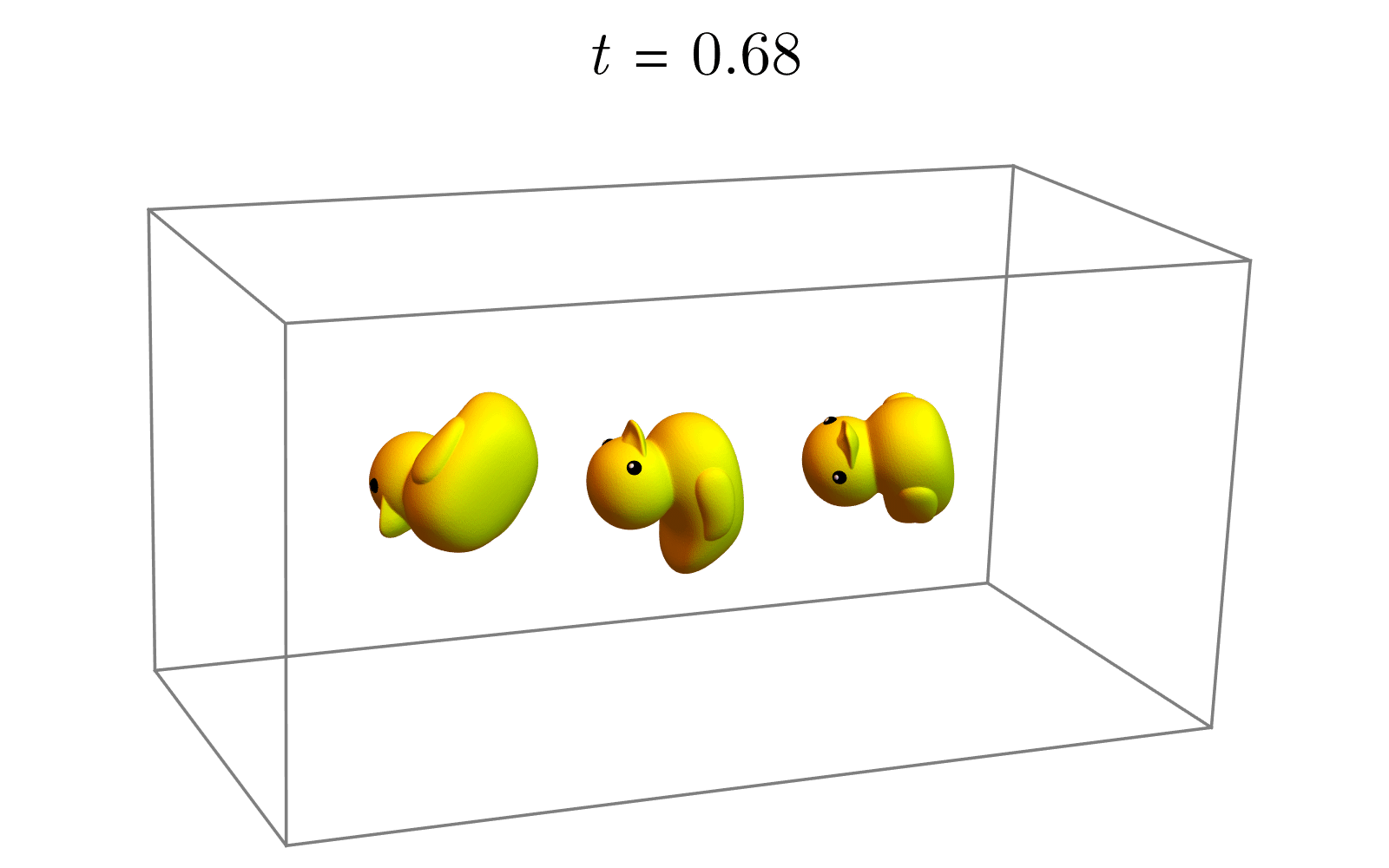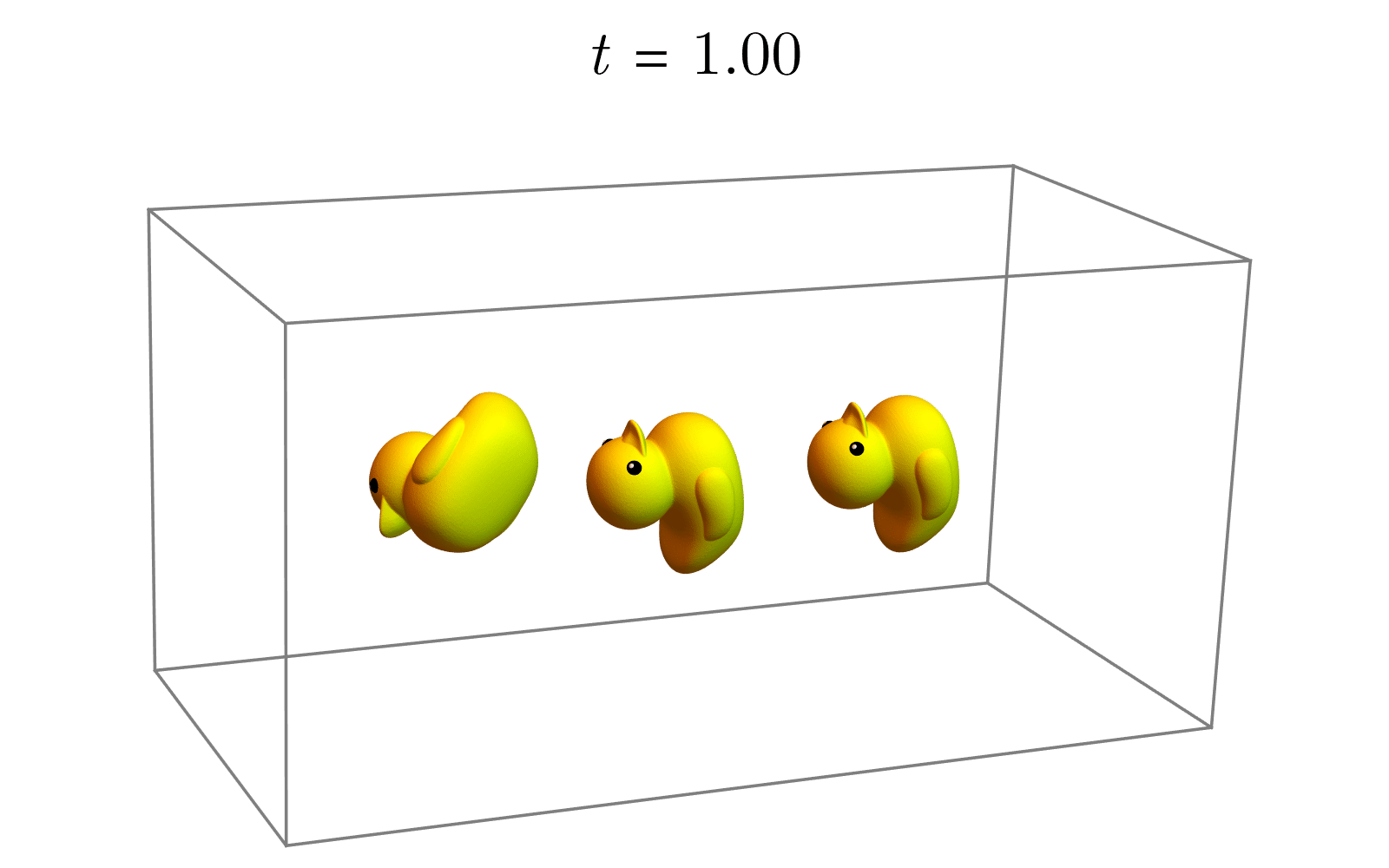
参考

[1] 封闭场景无人驾驶技术与应用.