(LeetCode 每日一题) 498. 对角线遍历 (矩阵、模拟)

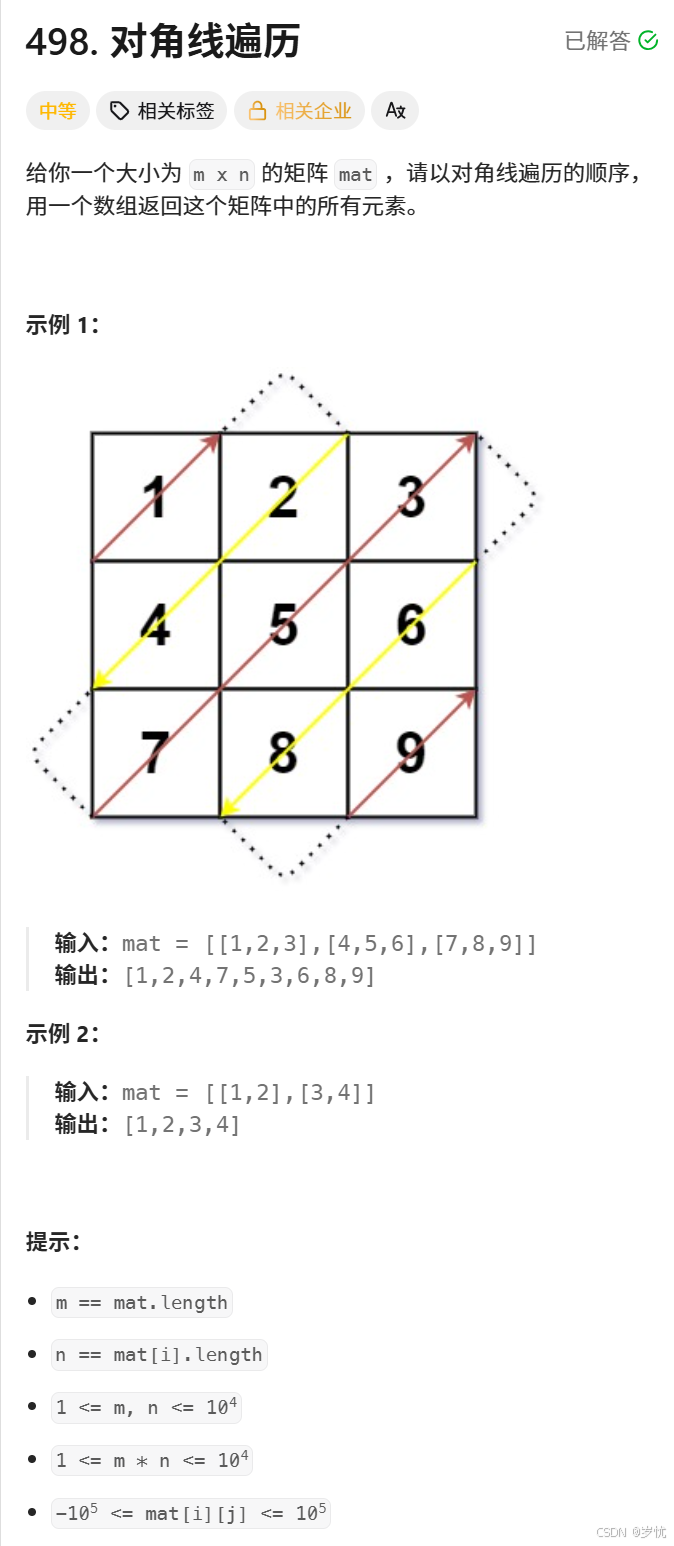
思路：矩阵模拟，时间复杂度0(nm)。
按对角线遍历，而每条对角线都是i+j=k，k的范围为[0,n-1+m-1]。

C++版本：

class Solution {
public:vector<int> findDiagonalOrder(vector<vector<int>>& mat) {int n=mat.size(),m=mat[0].size();vector<int> ans;// i+j=k  -> j=k-i;for(int k=0;k<n+m-1;k++){//枚举j的值，那需要求出j可达的最小值和最大值//当i=n-1时，j的值最小，但不能小于0int mn=max(k-(n-1),0);//当i=0时，j的值最大，但不能大于m-1int mx=min(k-0,m-1);if(k%2==0){for(int j=mn;j<=mx;j++){ans.push_back(mat[k-j][j]);}}else{for(int j=mx;j>=mn;j--){ans.push_back(mat[k-j][j]);}}}return ans;}
};

JAVA版本：

class Solution {public int[] findDiagonalOrder(int[][] mat) {int n=mat.length,m=mat[0].length;int[] ans=new int[n*m];int idx=0;// i+j=k  -> j=k-i;for(int k=0;k<n+m-1;k++){int mn=Math.max(k-(n-1),0);int mx=Math.min(k-0,m-1);if(k%2==0){for(int j=mn;j<=mx;j++){ans[idx++]=mat[k-j][j];}}else{for(int j=mx;j>=mn;j--){ans[idx++]=mat[k-j][j];}}}return ans;}
}

GO版本：

func findDiagonalOrder(mat [][]int) []int {n,m:=len(mat),len(mat[0])ans:=make([]int,n*m)idx:=0// i+j=k  -> j=k-i;for k:=0;k<n+m-1;k++ {mn:=max(k-(n-1),0)mx:=min(k-0,m-1)if k%2==0 {for j:=mn;j<=mx;j++ {ans[idx]=mat[k-j][j]idx++}}else{for j:=mx;j>=mn;j-- {ans[idx]=mat[k-j][j]idx++}}}return ans
}