Neural Network with Softmax output｜神经网络的Softmax输出

-----------------------------------------------------------------------------------------------

这是我在我的网站中截取的文章，有更多的文章欢迎来访问我自己的博客网站rn.berlinlian.cn，这里还有很多有关计算机的知识，欢迎进行留言或者来我的网站进行留言！！！

-----------------------------------------------------------------------------------------------
 

一、神经网络的Softmax输出的含义

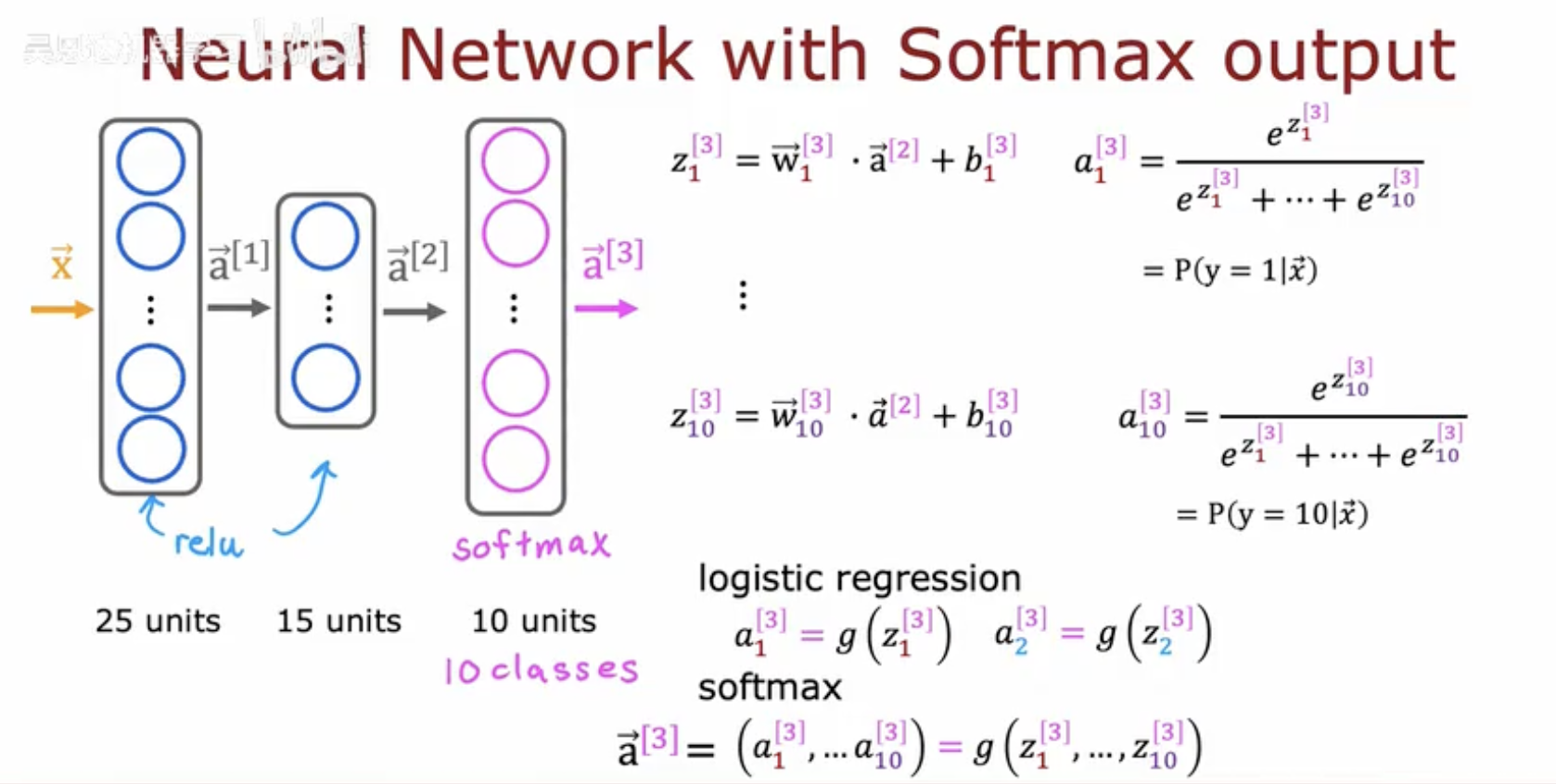
这张图片展示了神经网络中Softmax输出层的数学表达和结构设计。

1. 数学公式部分：

   • 第三层的输出 zi[3] 由权重 w‾i[3]​、前一层的激活值 a⃗[2] 和偏置 bi[3] 计算得到。

   • Softmax函数将 zi[3]​ 转换为概率 ai[3]，表示输入 x⃗ 属于类别 i 的概率 P(y=i∣x⃗)。

   • 公式中展示了10个类别的概率计算（i=1 到 10）。

2. 结构部分：

   • 网络结构为：输入层 → 25个隐藏单元 → 15个隐藏单元 → 10个输出单元（对应10个类别）。

   • 图中提到Logistic回归是Softmax在二分类时的特例，并对比了二者的激活函数形式。

3. 标注部分：

   • 底部标注了网络各层的单元数量（25 → 15 → 10）和最终的10分类任务

---

例子

1. 代码部分：

   • 模型结构为三层全连接网络：

     • 第一层：25个单元，ReLU激活。

     • 第二层：15个单元，ReLU激活。

     • 输出层：10个单元（对应MNIST的10类），Softmax激活。

   • 使用SparseCategoricalCrossentropy作为损失函数，并通过model.fit训练100轮。

   • 备注提示当前版本非最优（后续有改进方案）。

2. 理论步骤部分：

   • 步骤1：定义模型 fw,b(x⃗)（即网络结构）。

   • 步骤2：指定损失函数 L 和代价函数（如交叉熵）。

   • 步骤3：通过数据训练最小化 f(w⃗,b)（即优化权重和偏置）。

---

二、回归问题中数值舍入误差

1. 问题背景：

   • 在逻辑回归中，直接计算Sigmoid输出（a= 1 /（1+e−z））再代入交叉熵损失函数可能导致数值舍入误差，尤其是当z值极大或极小时（例如±1000）。

2. 改进方案：

   • 原始实现：
     使用Sigmoid激活函数（activation='sigmoid'），损失函数为：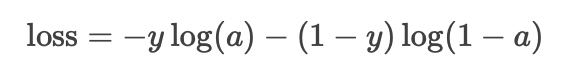

     

   • 更精确的实现：
     在代码中设置from_logits=True，直接基于未激活的原始分数zz计算损失，公式为：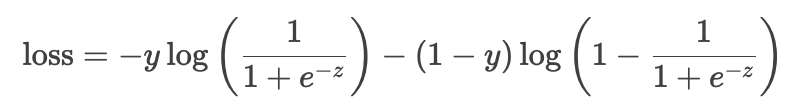

     

     这种方式避免了Sigmoid输出aa的显式计算，减少了数值误差。

3. 网络结构示例：

   • 图中展示了一个简单的三层网络（25 → 15 → 10单元），最后一层为Sigmoid激活。

---

Softmax回归中数值精度优化

1. Softmax回归公式：

   • 输出概率分布 (a1,...,a10)=g(z1,...,z10)，其中 g 是Softmax函数。

2. 原始损失函数：

   • 直接基于Softmax输出 a⃗ 计算交叉熵损失：

     

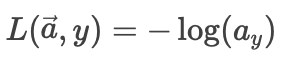
     其中 ayay​ 是真实类别 y 对应的概率值。

3. 数值更精确的实现：

   • 使用 from_logits=True 选项，直接基于原始分数 zi 计算损失，避免显式计算Softmax：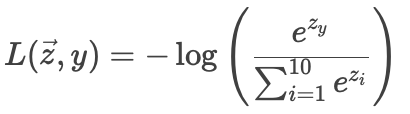

     

     这种方式减少了中间步骤的数值误差，尤其适用于极端值（如 zi 过大或过小）。

4. 代码实现：

   • 网络结构为三层全连接层（25 → 15 → 10单元），输出层使用Softmax激活。

   • 通过 model.compile 指定损失函数为 SparseCategoricalCrossentropy(from_logits=True)，以启用高精度计算模式。

---

例子（一）

这张图片展示了MNIST分类任务中一个数值计算更精确（numerically accurate）的TensorFlow实现方法，重点在于如何避免Softmax直接计算带来的数值问题。

1. 模型结构：

   • 使用三层全连接神经网络：

     • 前两层：25和15个ReLU激活单元。

     • 输出层：10个linear（无激活）单元，输出原始分数（logits，即z1到z10​），而非直接通过Softmax激活。

2. 损失函数配置：

   • 使用SparseCategoricalCrossentropy(from_logits=True)：

     • from_logits=True表示损失函数内部自动对logits（zi​）应用Softmax并计算交叉熵，避免显式计算Softmax的数值不稳定问题（如指数溢出）。

3. 预测阶段：

   • 模型直接输出logits（logits = model(X)）。

   • 需显式调用tf.nn.softmax(logits)将logits转换为概率分布（a1到a10​）。

对比与优势

• 传统方法：输出层用Softmax激活，直接计算概率，可能导致数值舍入误差。

• 改进方法：输出层保持线性，通过from_logits=True将Softmax计算合并到损失函数中，提升数值稳定性。

---

例子（二）

这张图片展示了逻辑回归（Logistic Regression）中数值计算更精确的实现方法，通过避免直接计算Sigmoid激活函数来提升数值稳定性。

1. 模型结构：

   • 使用三层全连接神经网络：

     • 前两层：25和15个Sigmoid激活单元。

     • 输出层：1个linear（无激活）单元，输出原始分数（logit，即z），而非直接通过Sigmoid激活。

2. 损失函数配置：

   • 使用BinaryCrossentropy(from_logits=True)：

     • from_logits=True表示损失函数内部自动对logit（z）应用Sigmoid并计算交叉熵，避免显式计算Sigmoid的数值问题（如极端值导致的梯度消失或溢出）。

3. 预测阶段：

   • 模型直接输出logit（logit = model(X)）。

   • 需显式调用tf.nn.sigmoid(logit)将logit转换为概率值（a）。

对比与优势

• 传统方法：输出层用Sigmoid激活，直接计算概率，可能导致数值不稳定。

• 改进方法：输出层保持线性，通过from_logits=True将Sigmoid计算合并到损失函数中，提升数值精度。

-----------------------------------------------------------------------------------------------

这是我在我的网站中截取的文章，有更多的文章欢迎来访问我自己的博客网站rn.berlinlian.cn，这里还有很多有关计算机的知识，欢迎进行留言或者来我的网站进行留言！！！

-----------------------------------------------------------------------------------------------