扩展卡尔曼滤波（EKF）的一阶泰勒展开（雅可比矩阵）详解

1. 雅可比矩阵介绍

概念
雅可比矩阵（Jacobian Matrix）是向量值函数的一阶偏导数构成的矩阵。对于一个从 $R^n$ 映射到 $R^m$ 的向量函数 F(x) ，其雅可比矩阵定义为：

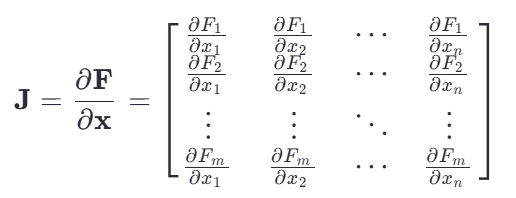
核心原理
雅可比矩阵的本质是提供多变量函数在某一点的最佳线性近似，对于函数 F(x) ，在点 a 附近的线性近似为：
F(x)≈F(a)+J(a)(x−a)

作用与效果
雅可比矩阵描述了输入空间的小变化如何映射到输出空间，表示了在局部区域内，函数如何"拉伸"、"旋转"和"扭曲"空间，雅可比行列式（矩阵的行列式）表示了局部体积的变化率和方向，即雅可比矩阵的每个元素$\frac{\partial F_i}{\partial x_j}$ 表示当第 j 个输入变量发生微小变化时，第 i 个输出变量的变化率，在以下场景中至关重要：

• 评估系统对参数变化的敏感度
• 分析系统的稳定性
• 优化问题中确定搜索方向

2. EKF-SLAM回顾

在EKF-SLAM中，需要对非线性的运动模型和观测模型进行一阶泰勒展开，以实现线性化处理。泰勒展开的核心是计算雅可比矩阵，它提供了函数在某一点的局部线性近似。

状态向量：

$x={\left[\begin{array}{ccccc}{s}^T& m_1^T& m_2^T& \cdots & m_n^T\end{array}\right]}^T$

其中：

• $s=[x,y,\theta {]}^T$ 是机器人位姿（2D平面）
• $m_i^T=[m_{x,i},m_{y,i}{]}^T$ 是第 i 个路标的坐标
• n 是路标总数

算法流程

1. 预测步骤：
   • 预测状态
   • 计算雅可比矩阵 $F_t$（对 $x_{t-1}$ 求导）
   • 预测协方差
2. 更新步骤（对于每个观测到的路标 i ）：
   • 计算观测预测
   • 计算雅可比矩阵 $H_t$ （对 $x_t$ 求导）
   • 计算卡尔曼增益
   • 更新状态
   • 更新协方差

3.运动模型及其雅可比矩阵

3.1 运动模型

运动模型描述了机器人如何根据控制输入 $u_t$，从 $x_{t-1}$ 移动到 $x_t$：
${\mathbf{x}}_t=f({\mathbf{x}}_{t-1},{\mathbf{u}}_t)+{\mathbf{w}}_t$
​其中 $w_t$ 是过程噪声，假设使用简单的速度运动模型，模型如下：

$f_x(x_{t-1},u_t)=\left[\begin{array}{c}{x}_{t-1}+v_t\Delta t\cos ({\theta }_{t-1}+{\omega }_t\Delta t/2)\\ y_{t-1}+v_t\Delta t\sin ({\theta }_{t-1}+{\omega }_t\Delta t/2)\\ {\theta }_{t-1}+{\omega }_t\Delta t\end{array}\right]$

其中 $u_t=[v_t,{\omega }_t{]}^T$ 是线速度和角速度。

3.2 雅可比矩阵
运动模型的雅可比矩阵 $F_t$ 是对前一时刻的状态 $x_{t-1}$ 求偏导，在估计值 ${\hat{x}}_{t-1|t-1}$ 处计算：

${\mathbf{F}}_t={\frac{\partial f({\mathbf{x}}_{t-1},{\mathbf{u}}_t)}{\partial {\mathbf{x}}_{t-1}}|}_{{\hat{\mathbf{x}}}_{t-1|t-1}}$

由于运动只影响机器人位姿，不影响地图特征，雅可比矩阵为分块结构：

${\mathbf{F}}_t=\left[\begin{array}{ccccc}\frac{\partial f_s}{\partial x}& 0_{3\times 2}& 0_{3\times 2}& \cdots & 0_{3\times 2}\\ 0_{2\times 3}& {\mathbf{I}}_2& 0_{2\times 2}& \cdots & 0_{2\times 2}\\ 0_{2\times 3}& 0_{2\times 2}& {\mathbf{I}}_2& \cdots & 0_{2\times 2}\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ 0_{2\times 3}& 0_{2\times 2}& 0_{2\times 2}& \cdots & {\mathbf{I}}_2\end{array}\right]$

其中，机器人位姿部分的雅可比子矩阵为：

$\frac{\partial f_t}{\partial \mathbf{x}}=\left[\begin{array}{ccc}1& 0& -v_t\Delta t\sin ({\theta }_{t-1}+{\omega }_t\Delta t/2)\\ 0& 1& v_t\Delta t\cos ({\theta }_{t-1}+{\omega }_t\Delta t/2)\\ 0& 0& 1\end{array}\right]$

3.3 说明
运动模型雅可比矩阵的特点：

• 只有机器人位姿部分有非零元素
• 地图特征部分为单位矩阵，表示运动不影响地图特征

在预测步骤中，需要计算状态预测的协方差：
$P_{t\mid t-1}=F_t{P}_{t-1\mid t-1}{F}_t^T+Qt$

这里 $F_t$ 表示前一时刻状态的微小变化如何影响当前时刻的状态预测，因此需要对 $x_{t-1}$ 求导，用于状态预测和协方差预测。

4. 观测模型及其雅可比矩阵

4.1 观测模型
观测模型描述了机器人如何观测环境中的路标：

${\mathbf{z}}_t=h({\mathbf{x}}_t)+{\mathbf{v}}_t$

其中 $v_t$ 是观测噪声，假设观测到路标 i ，观测模型的极坐标形式为：

$h({\mathbf{x}}_t)=\left[\begin{array}{c}\sqrt{(m_{x,i}-x_t{)}^2+(m_{y,i}-y_t{)}^2}\\ {\tan }^{-1}\left(\frac{m_{y,i}-y_t}{m_{x,i}-x_t}\right)-{\theta }_t\end{array}\right]=\left[\begin{array}{c}r\\ \varphi \end{array}\right]$

其中 r 是距离，ϕ 是角度。

4.2 雅可比矩阵
观测模型的雅可比矩阵 $H_t$ 是对当前时刻的状态 $x_t$求偏导，在预测值 ${\hat{x}}_{t\mid t-1}$处计算：

${\mathbf{H}}_t={\frac{\partial h({\mathbf{x}}_t)}{\partial {\mathbf{x}}_t}|}_{{\hat{\mathbf{x}}}_{t|t-1}}$

雅可比矩阵也是分块结构，只对机器人位姿和被观测路标位置有非零元素：

${\mathbf{H}}_t=\left[\begin{array}{cccccc}\frac{\partial h}{\partial \mathbf{s}}& 0& \cdots & \frac{\partial h}{\partial {\mathbf{m}}_i}& \cdots & 0\end{array}\right]$

其中：$\frac{\partial h}{\partial \mathbf{s}}$ 是观测模型对机器人位姿的雅可比子矩阵
$\frac{\partial h}{\partial {\mathbf{m}}_i}$是观测模型对路标 i 位置的雅可比子矩阵
具体计算：
令 $d=\sqrt{(m_{x,i}-x_t{)}^2+(m_{y,i}-y_t{)}^2}$
​
表示机器人到路标的距离，则：

$\frac{\partial h}{\partial \mathbf{s}}=\left[\begin{array}{ccc}-\frac{m_{x,i}-x_t}{d}& -\frac{m_{y,i}-y_t}{d}& -1\\ \frac{m_{y,i}-y_t}{d^2}& -\frac{m_{x,i}-x_t}{d^2}& 0\end{array}\right]$

$\frac{\partial h}{\partial {\mathbf{m}}_i}=\left[\begin{array}{cc}\frac{m_{x,i}-x_t}{d}& \frac{m_{y,i}-y_t}{d}\\ -\frac{m_{y,i}-y_t}{d^2}& \frac{m_{x,i}-x_t}{d^2}\end{array}\right]$

4.2 解释说明

观测模型雅可比矩阵的特点：

• 只对机器人位姿和被观测路标有非零导数
• 对其他路标的导数为零（条件独立性）
• 这体现了SLAM问题中的稀疏结构
• 当观测到新路标时，需要扩展状态向量并初始化新路标

在更新步骤中，需要计算卡尔曼增益：
$K_t=P_{t\mid t-1}{H}_t^T(H_t{P}_{t\mid t-1}{H}_t^T+R_t{)}^{-1}$

这里 $H_t$ 表示当前状态的微小变化如何影响观测预测，因此需要对 $x_t$ 求导，用于计算卡尔曼增益和状态更新。