考研复习-计算机组成原理-第二章-数据的表示和运算
本文章仅作王道408书上没有的内容的补充
带符号整数的乘法
均使用补码表示乘数和被乘数
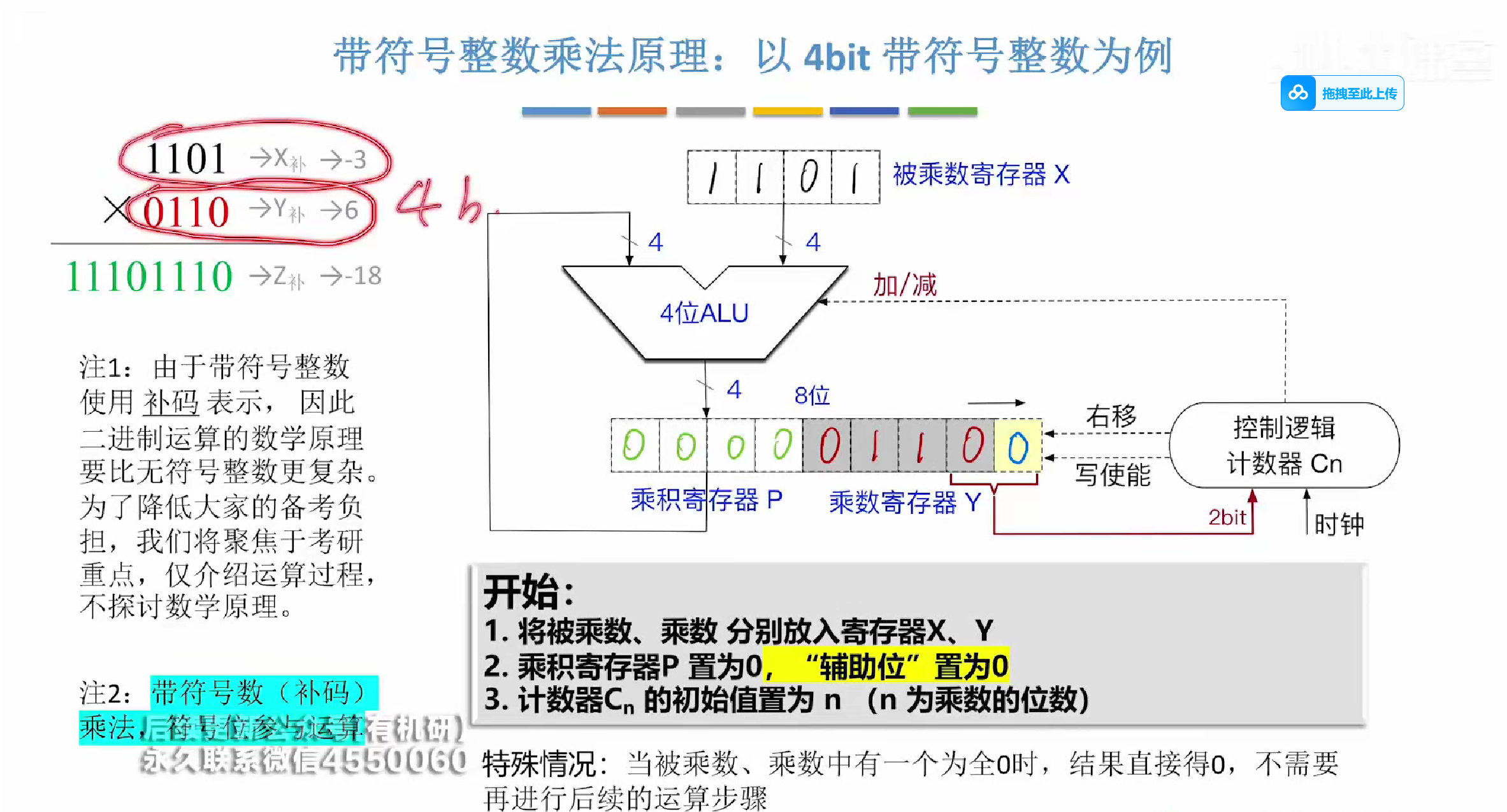
示例
一开始先将乘数和辅助位放入
控制逻辑根据Y中的最后两位判断行事逻辑
操作逻辑表如作图所示
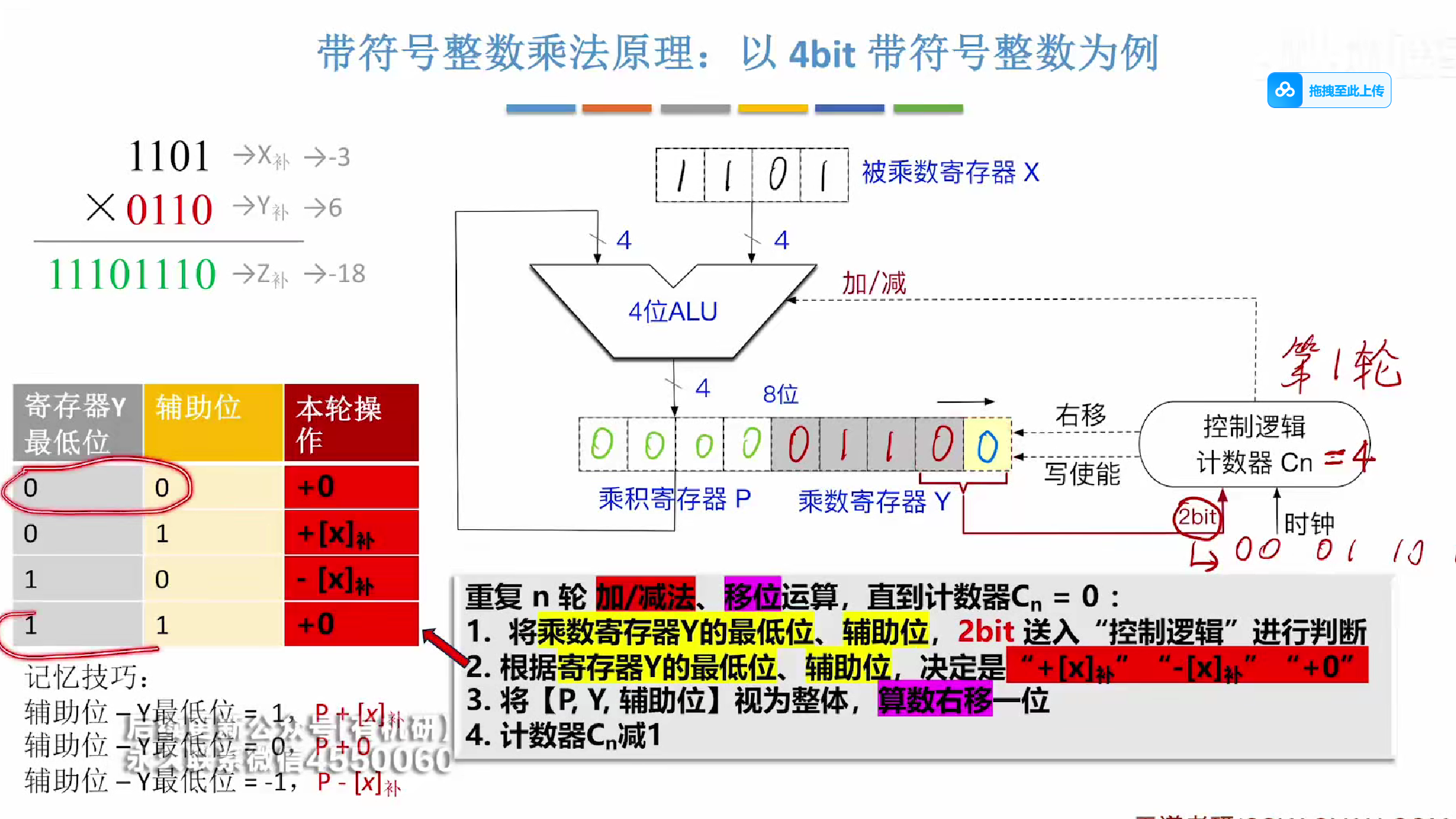
第一轮一开始是00,所以什么也不加,让寄存器保持原样
然后右移寄存器,高位补符号位,低位溢出舍弃
cn-1=4-1=3
第二趟
此时我们发现指令是10
对应的操作是-x补
那么如右上所示
p-x补
可以等价为
p+[-x]补
即按位取反+1
得到结果写入乘积寄存器
然后算数右移
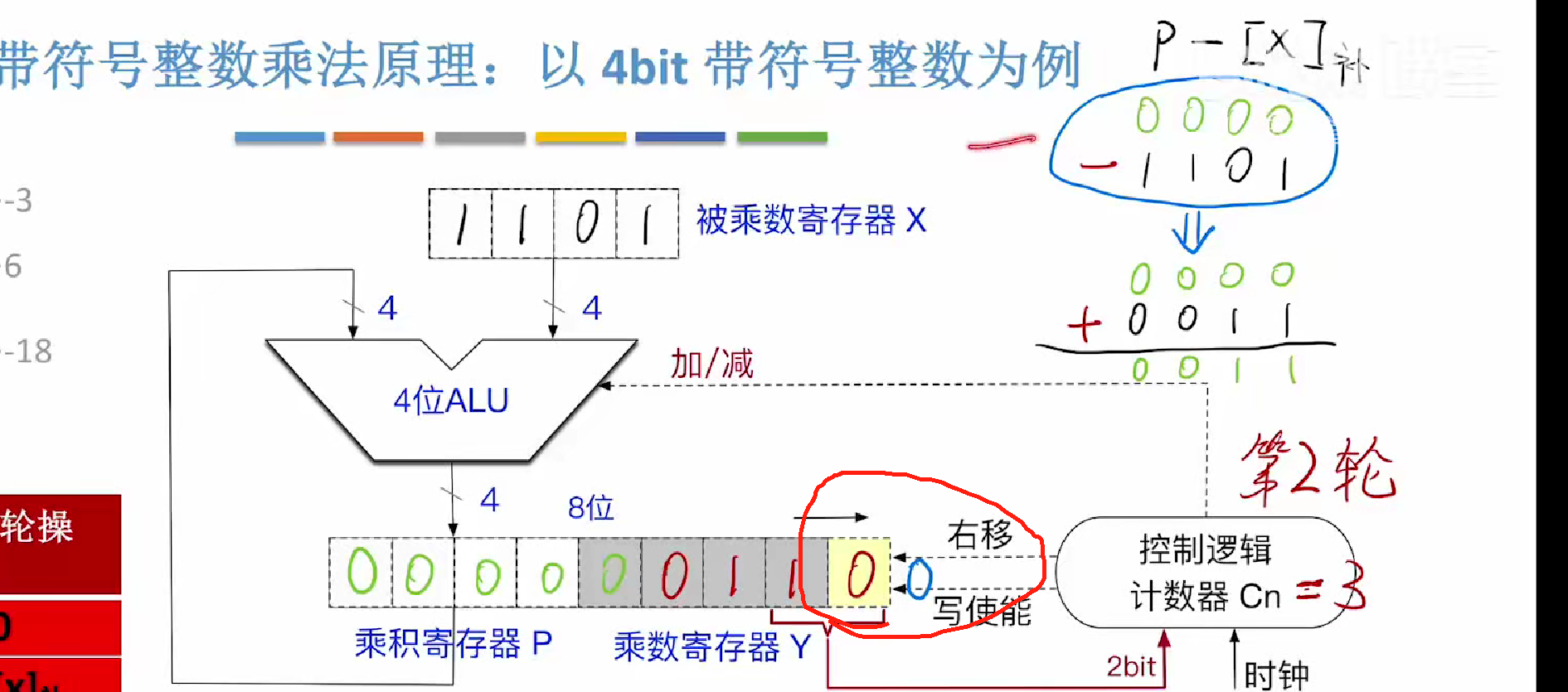
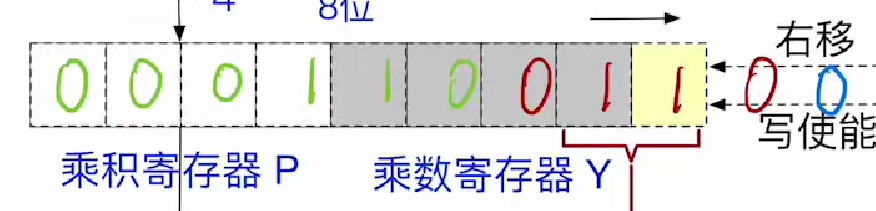
第三轮由于是11信号
直接右移即可

第四轮是+补码
1101写入p中
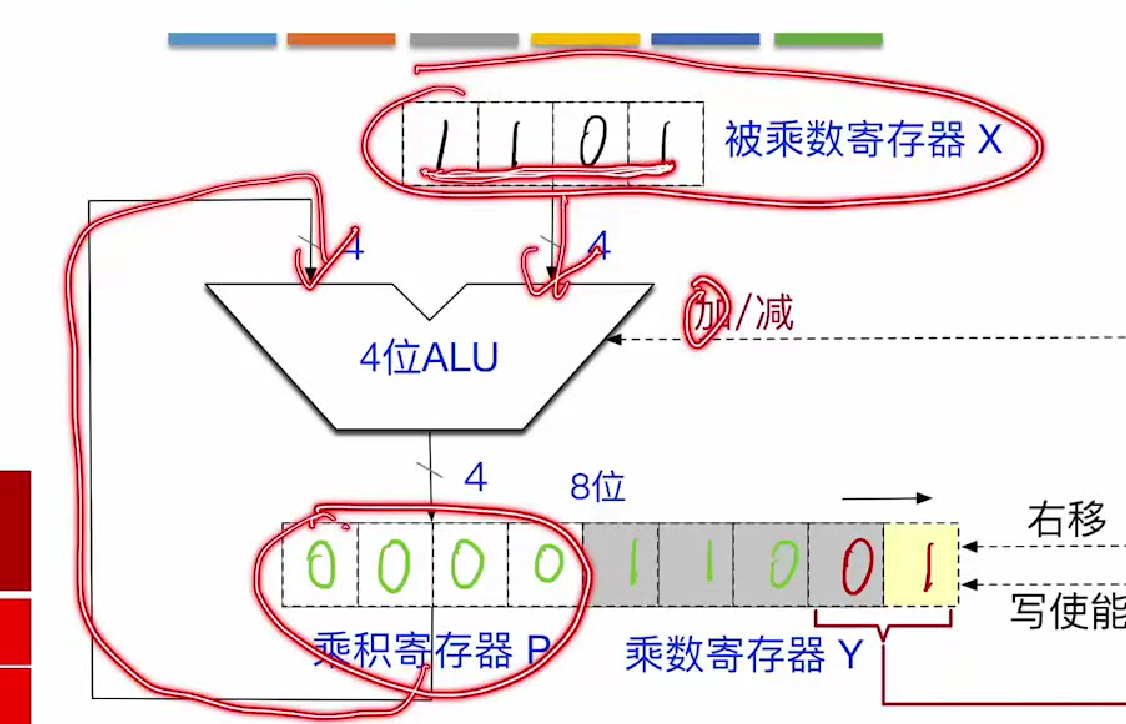
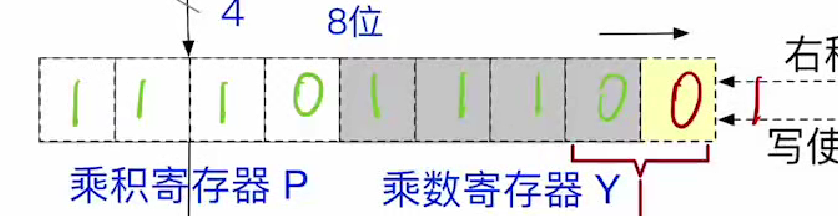
第五轮右移
然后前面补充符号位
此时cn=0,不再有后续
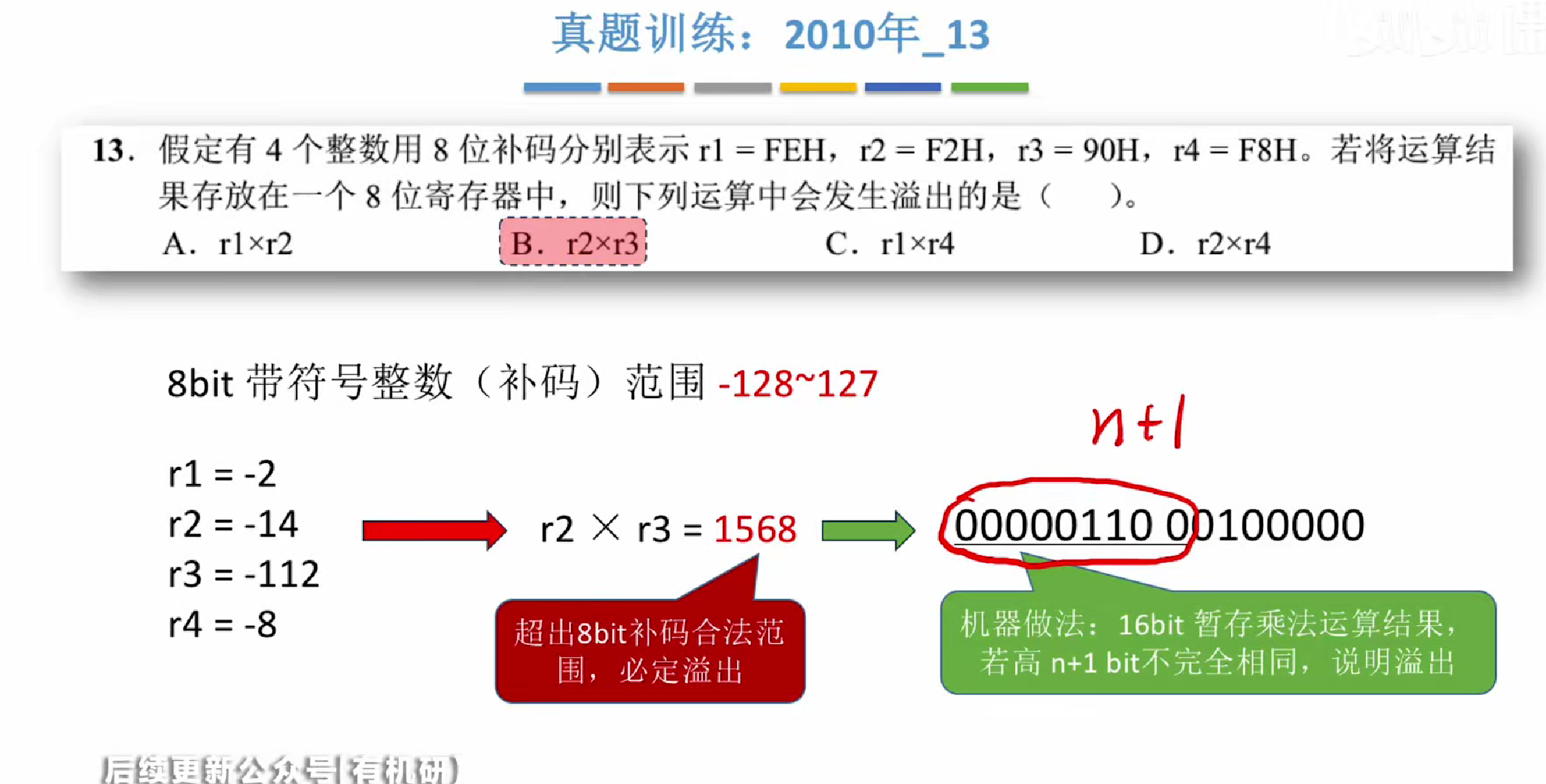
溢出判断
其中cf常用于判断无符号加法,所以对于乘法我们依旧使用of进行判断
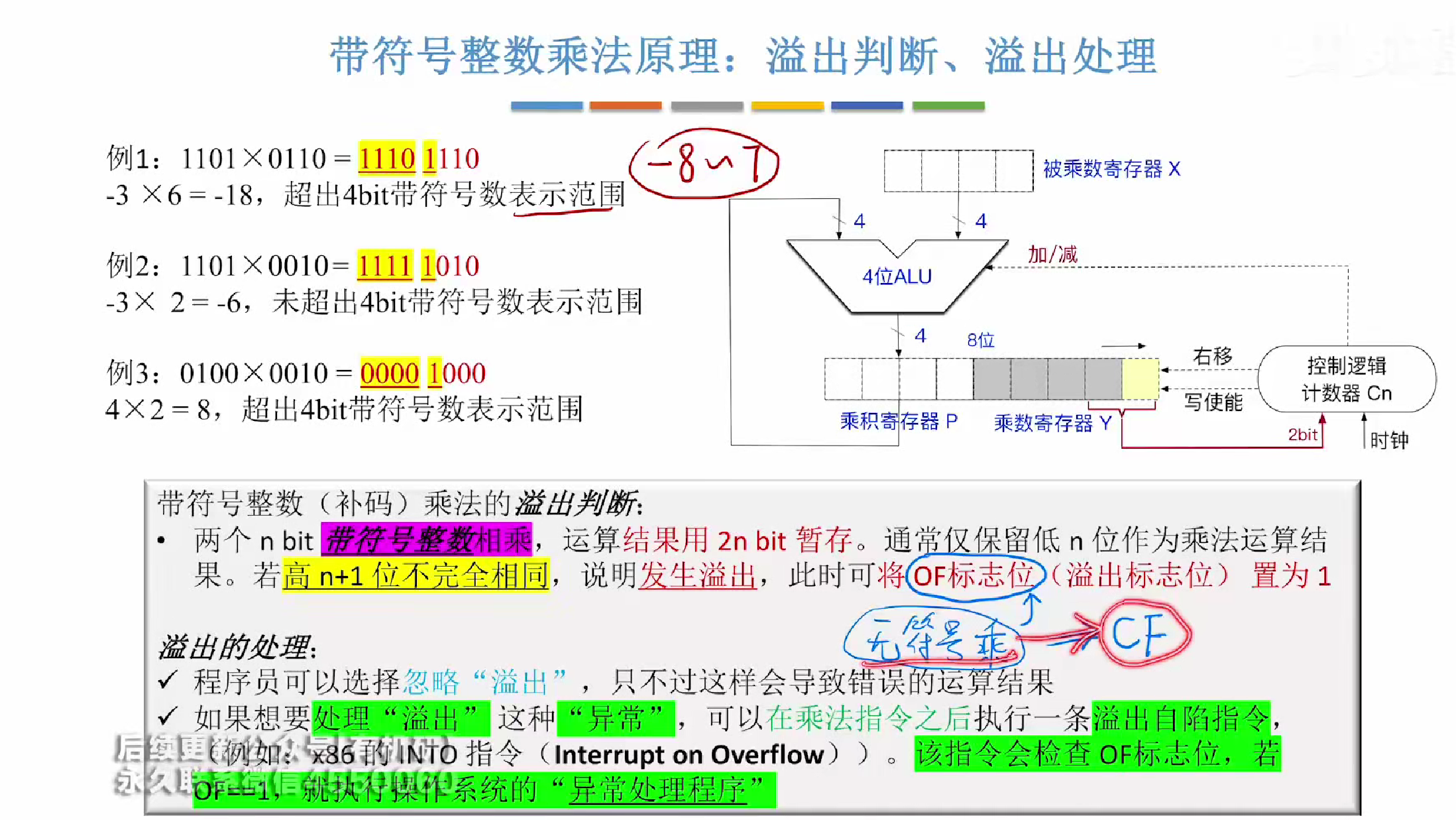
也可以直接使用手算的方式,补码范围我们已经知道
那么我们直接人工算出乘积后在范围内进行判断
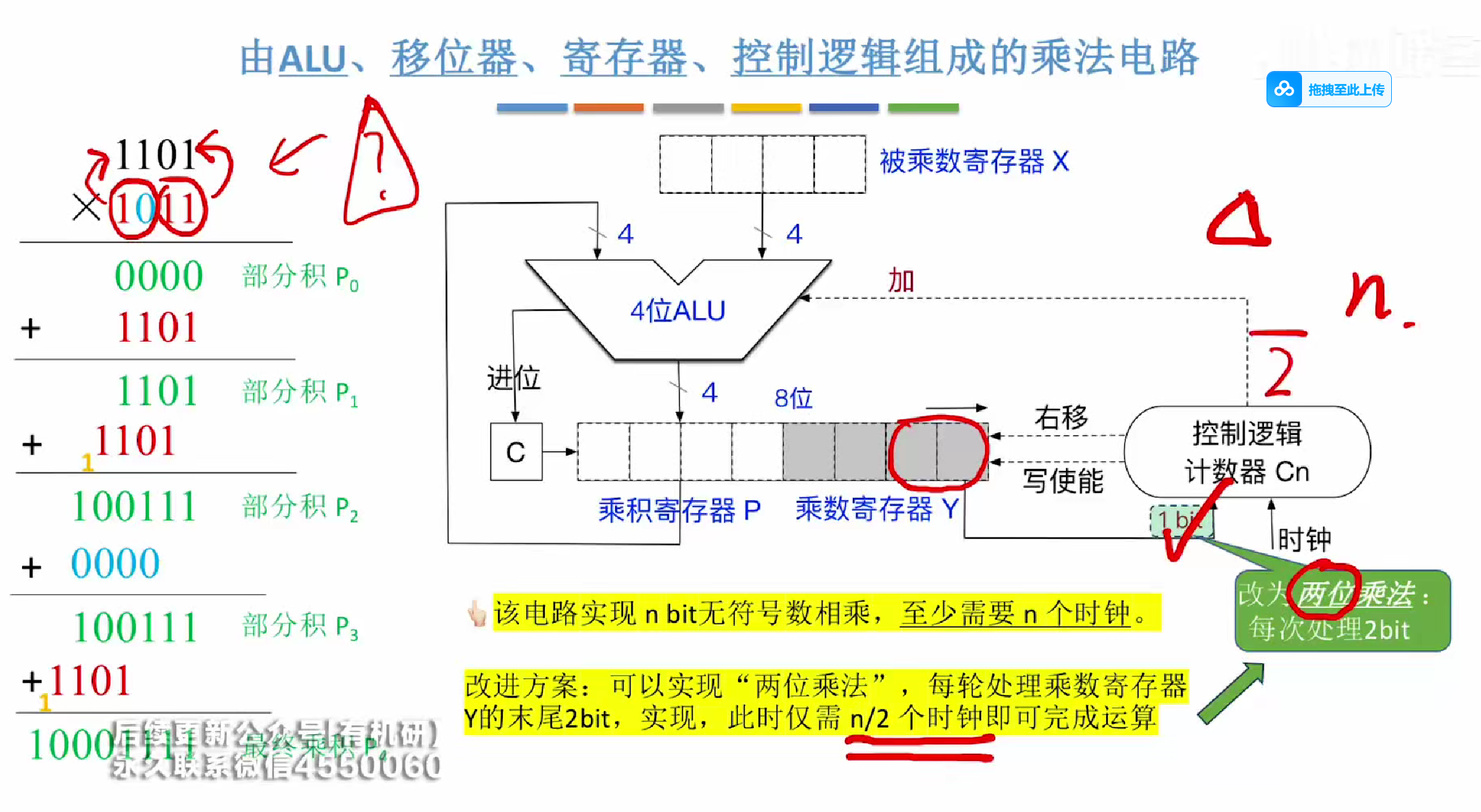
常见乘法运算电路
可以一次性对两位数进行运算
缩短时钟周期为原来的一半
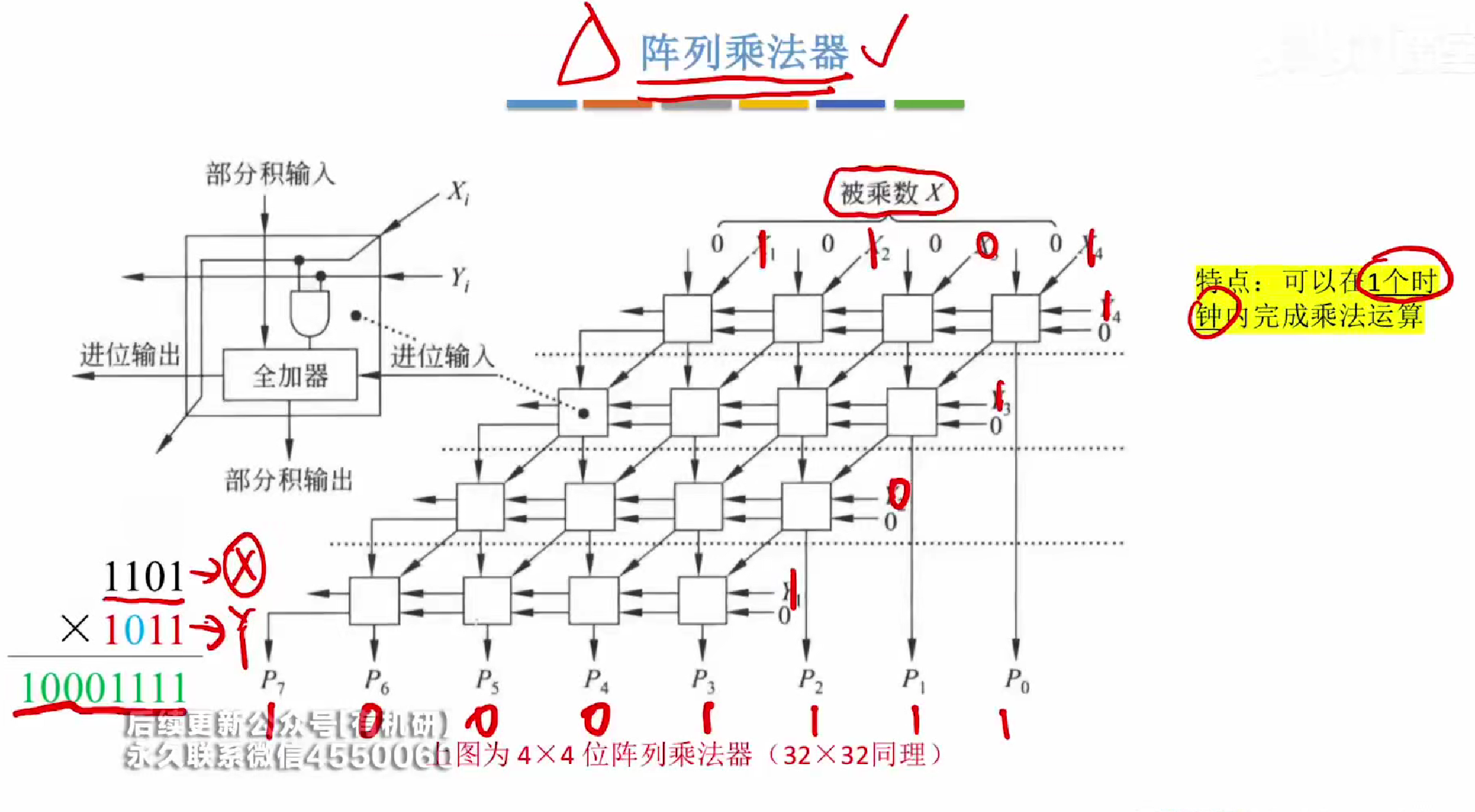
阵列乘法器
软件逻辑实现乘法

总结

除法电路(难点)
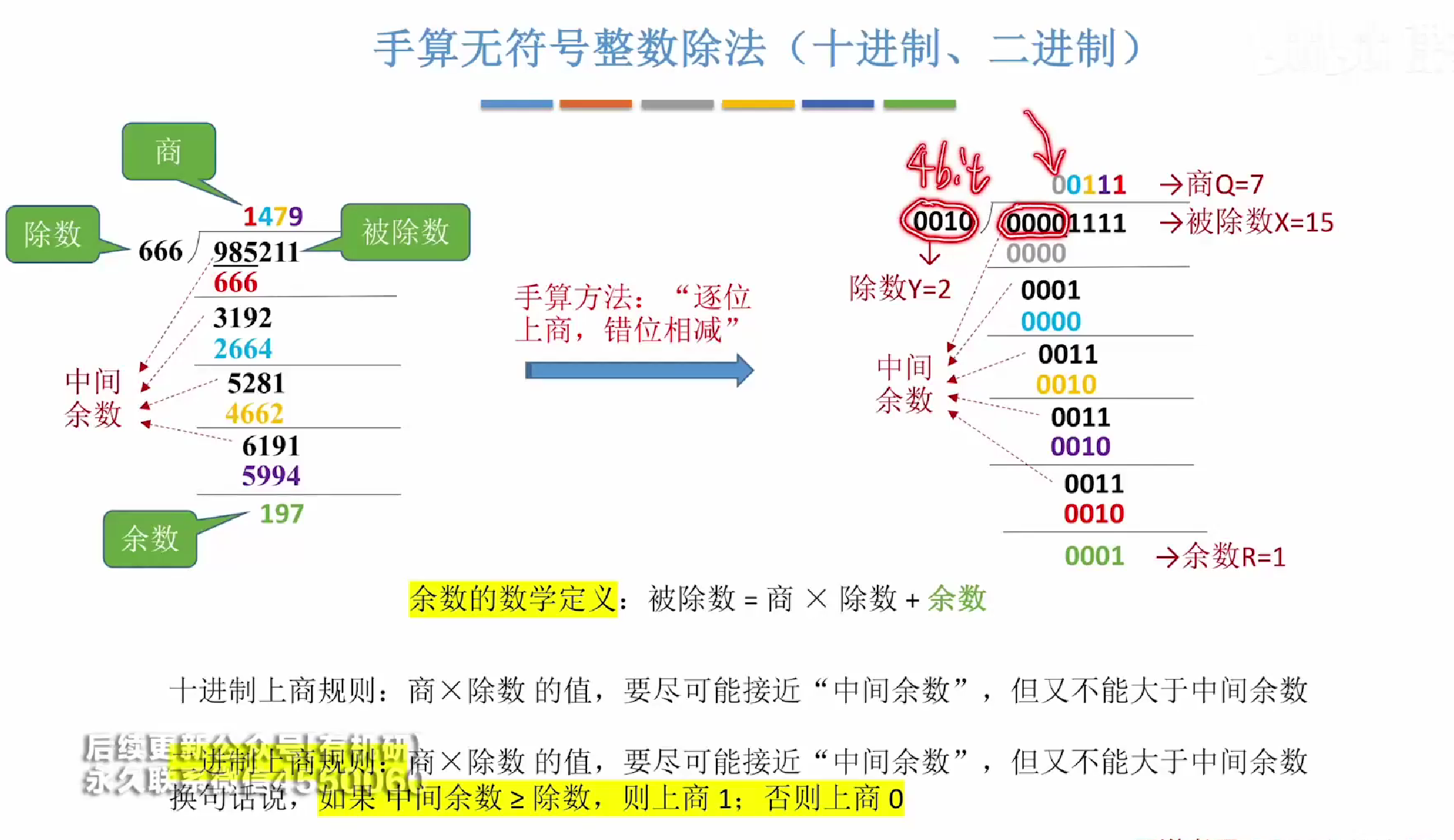
手算无符号整数除法

除法运算电路实例
1.初始时,先将除数和被除数放入对应电路的位置
若被除数不足寄存器位数,则进行零扩展
如图所示
以及初始的异常检查
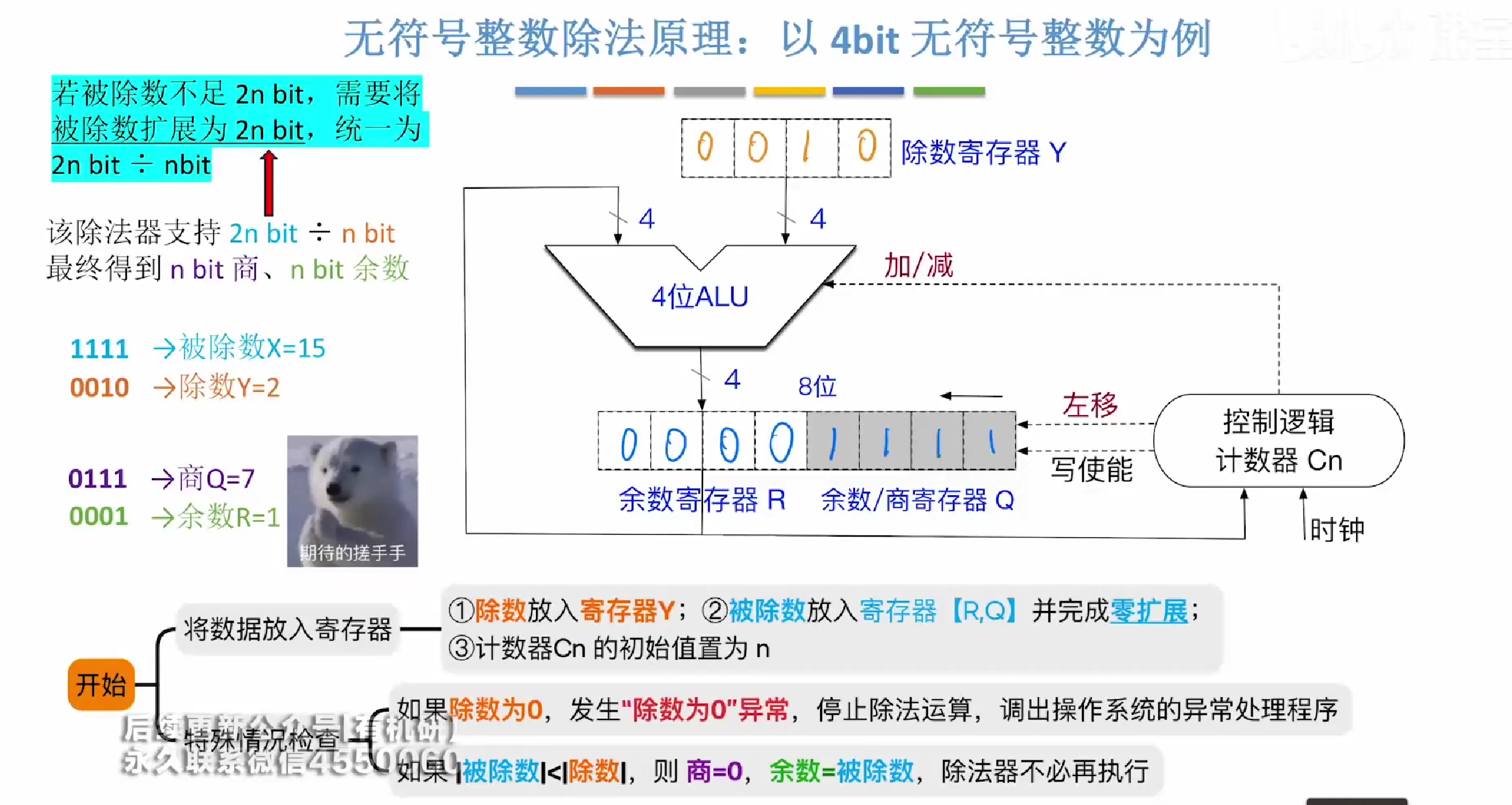
第一趟处理
注意,,因为商寄存器最终只能够保存n为商,而我们手算的过程中我们可以发现我们会得到n+1位的商,所以我们需要将第一位商进行舍弃。
所以在运算过程中,我们需要对第一位进行一次判断,判断是否为1,如果为1则发生溢出,停止除法运算
为0则继续
而如何上商的规则,我们手算很好判断,那么对于计算机来说,我们判断的标准是,判断R-Y的值是否>=0如果≥那么我们直接上1,代表着被除数此时现在能够上商
如果不等,那么则直接上0
如图所示第一轮时,我们判断0000-0010小于0,则我们直接上0,此时R中存放的是R-Y
并非我们下一个需要进行计算的数,我们需要再进行一次+Y保持原样
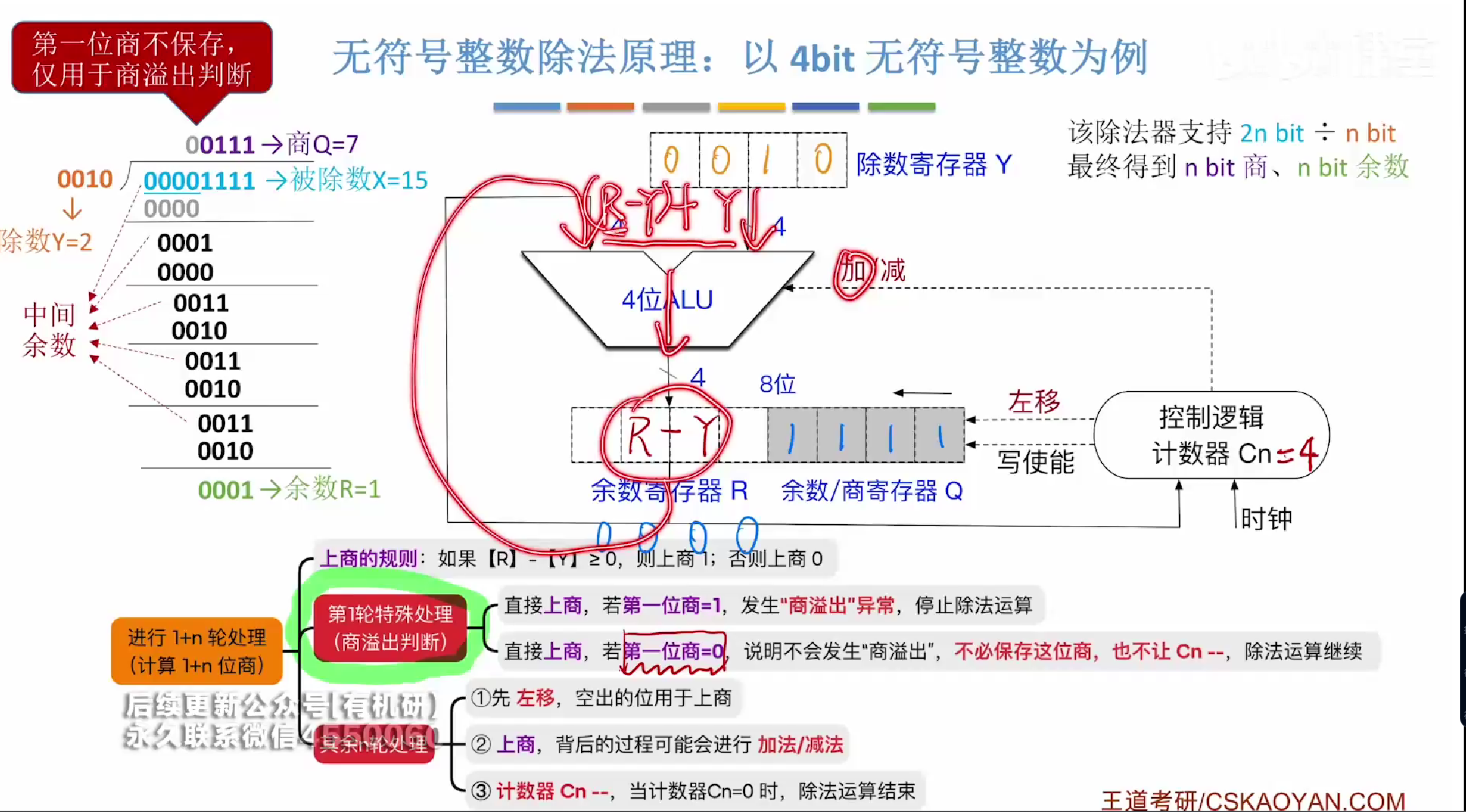
除了第一轮之外,其余轮数的处理如上图下方所示的三种,其中左移是必要的
先进行左移
第二轮
然后此时判断R中的值是否>=y
我们发现0001小于y所以
此时末尾的空缺位置上0
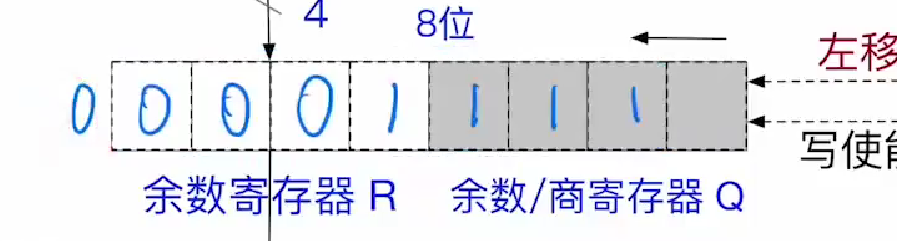
第三轮
开始时先进行左移运算
得到如图所示的结果
此时我们判断R-Y是否>=0
发现此时R>=Y
所以此时我们应该上商1
即末尾补1
再将运算结果即0011-除数0010
得到的0001写入寄存器当中

如图所示
第三趟结束
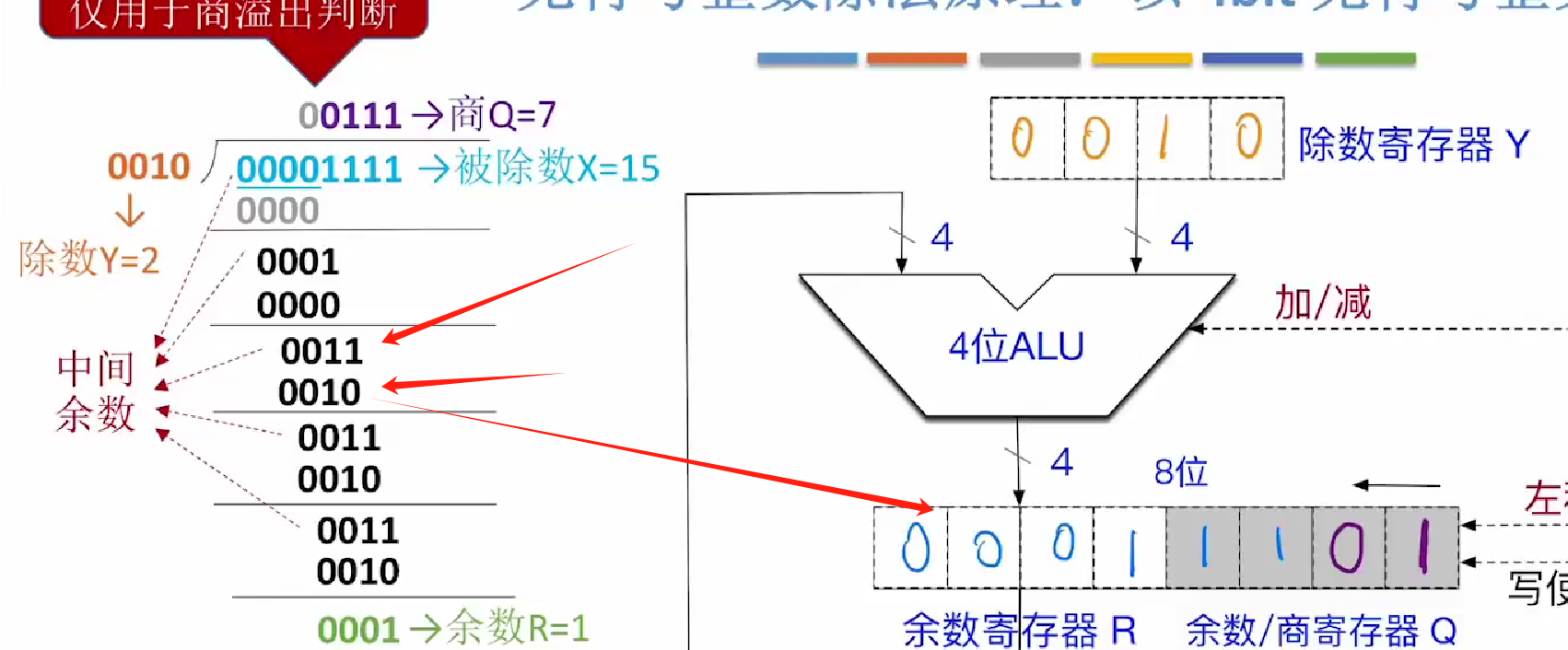
第四轮如图所示
运算完毕之后的值
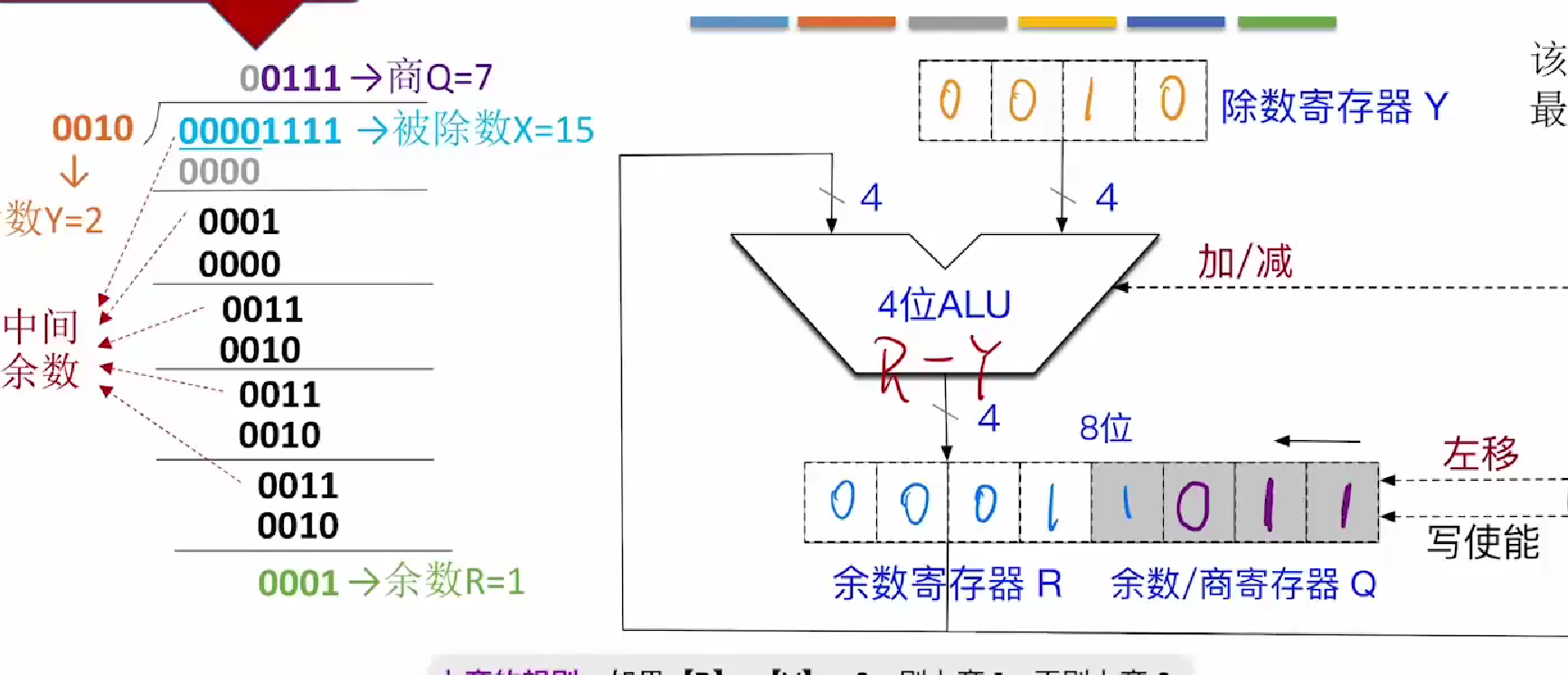
第五轮
除法运算结束此时cn=0(注意cn依旧=4,只是第一轮不进行cn--)
此时R中保存的就是正确的余数
商寄存器为正确的商
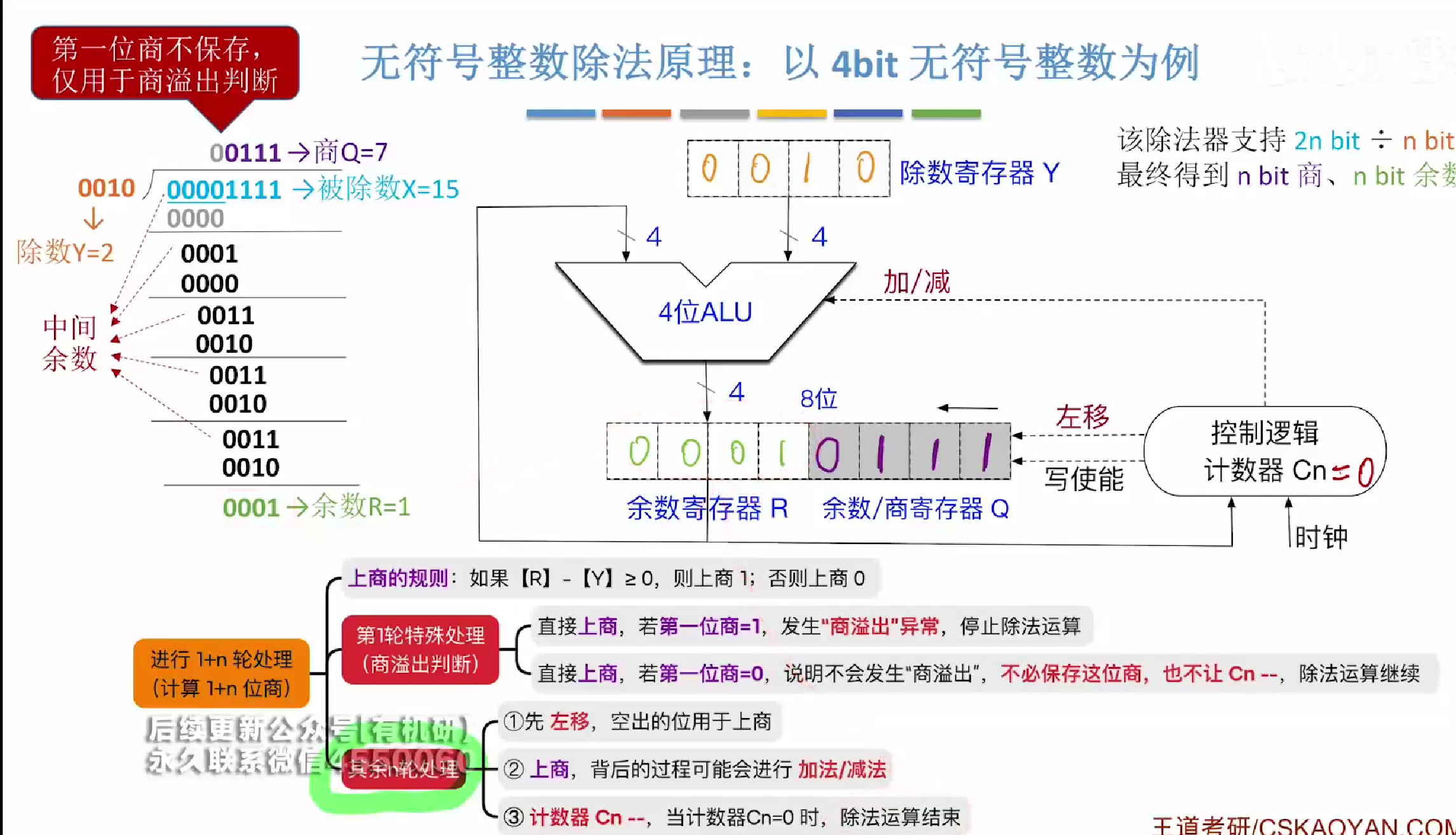
其中我们发现,每一轮运算中我们都需要进行R-Y的运算,将其运算结果放入余数寄存器R中
如果大于0则上商1,并将运算结果保留在R中
如果小于0则上商0,此时R中的R-Y是负数,是错误的,因为我们实际上是减去的0000,那么我们需要将错误减去的Y重新加回去复原R
这种做法叫做恢复余数法。
重点理解

对于做题
如果出题人让我们计算商和余数分别是多少
我们可以先进行十进制的运算
然后把他转化为32位的无符号整数即可
余数和商都是这样
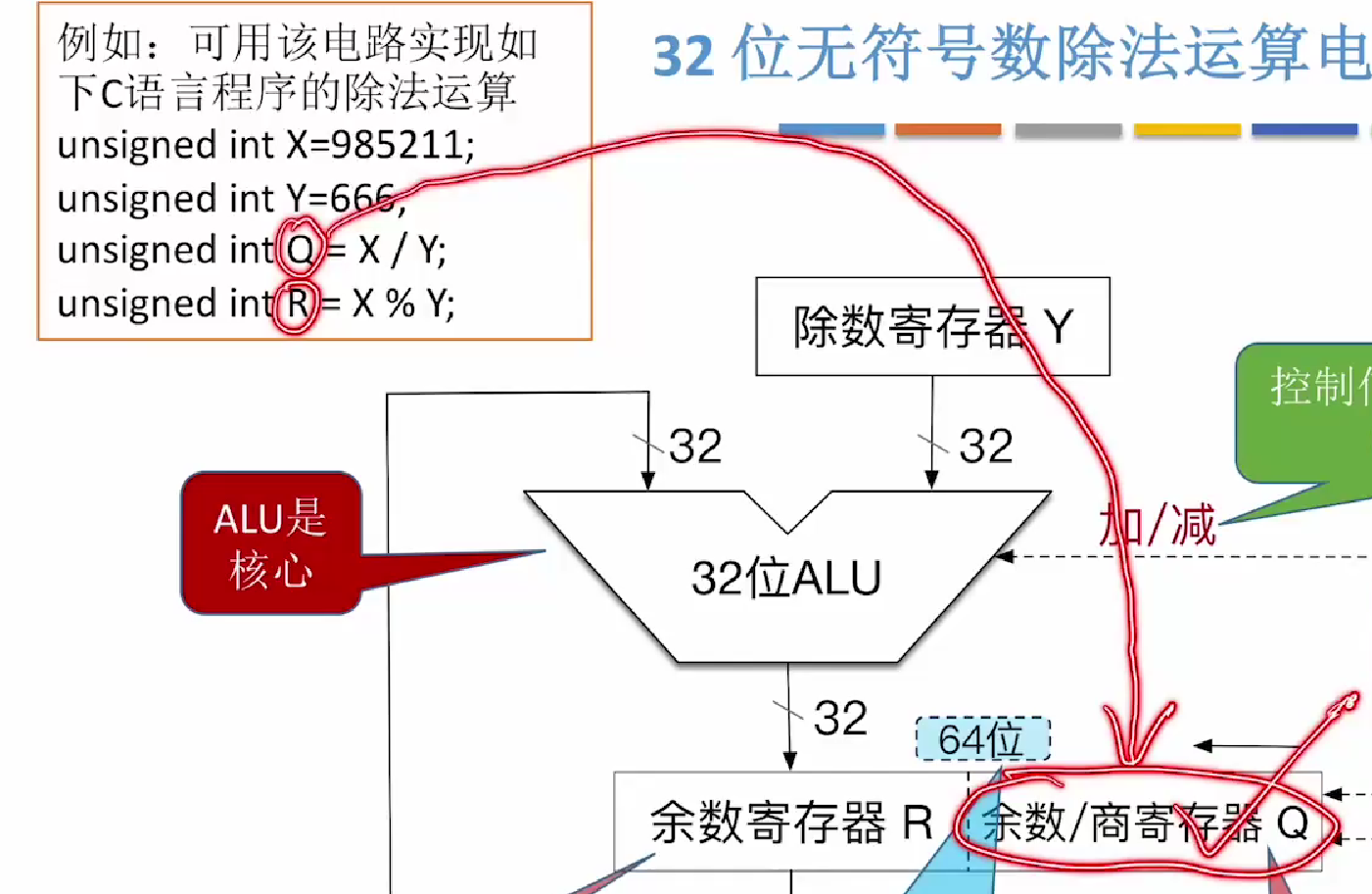
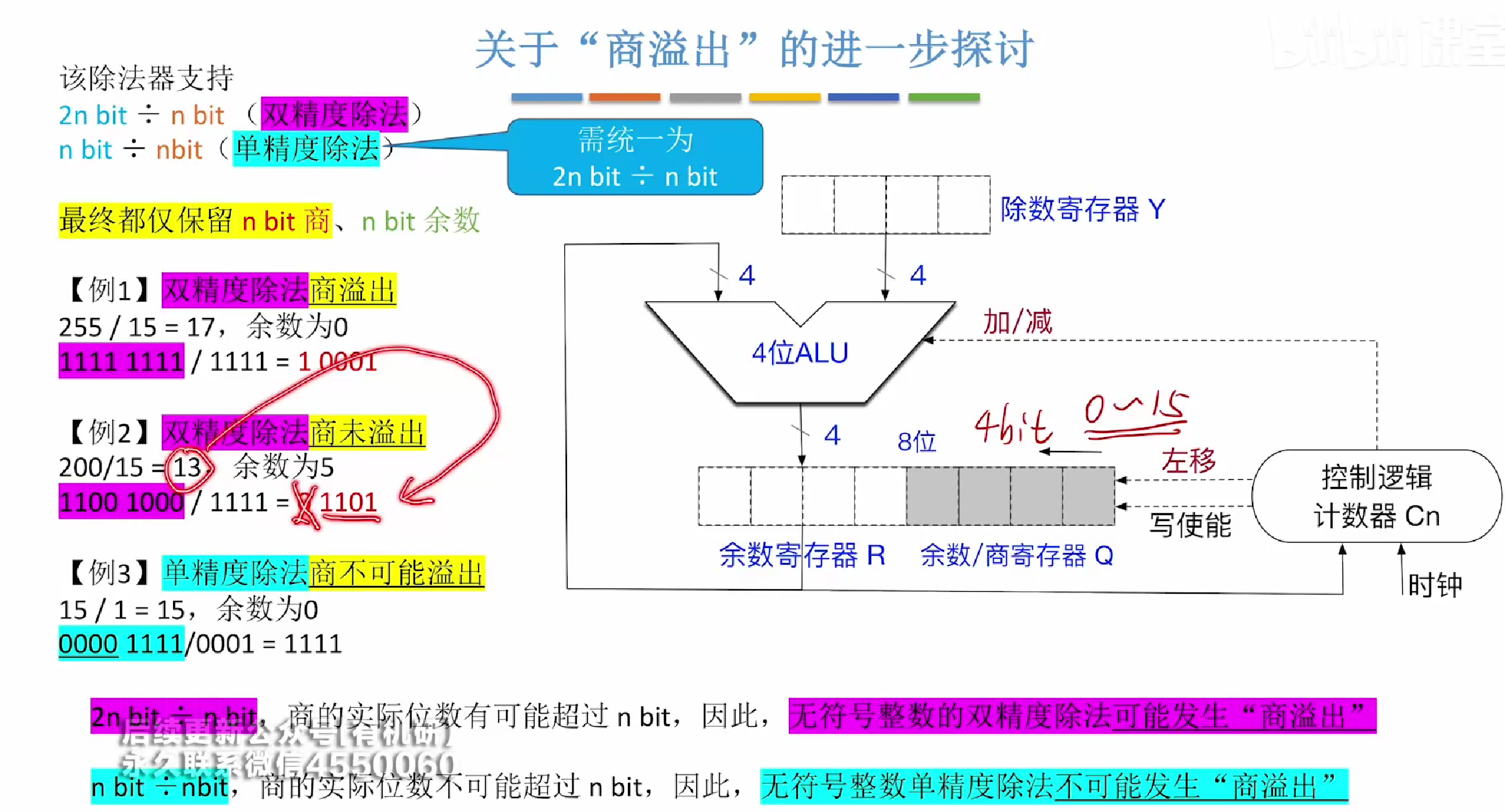
其中关于商溢出的判断也是如此,我们可以先进行十进制的算法
然后再根据商的最大表示范围判断商是否大于范围
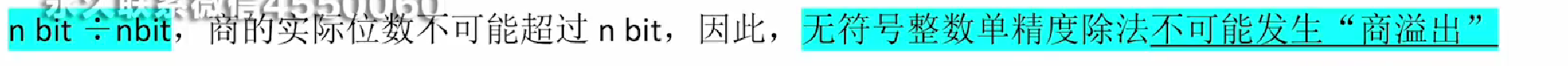
因为4位÷4位最多就是4位商,不怕溢出
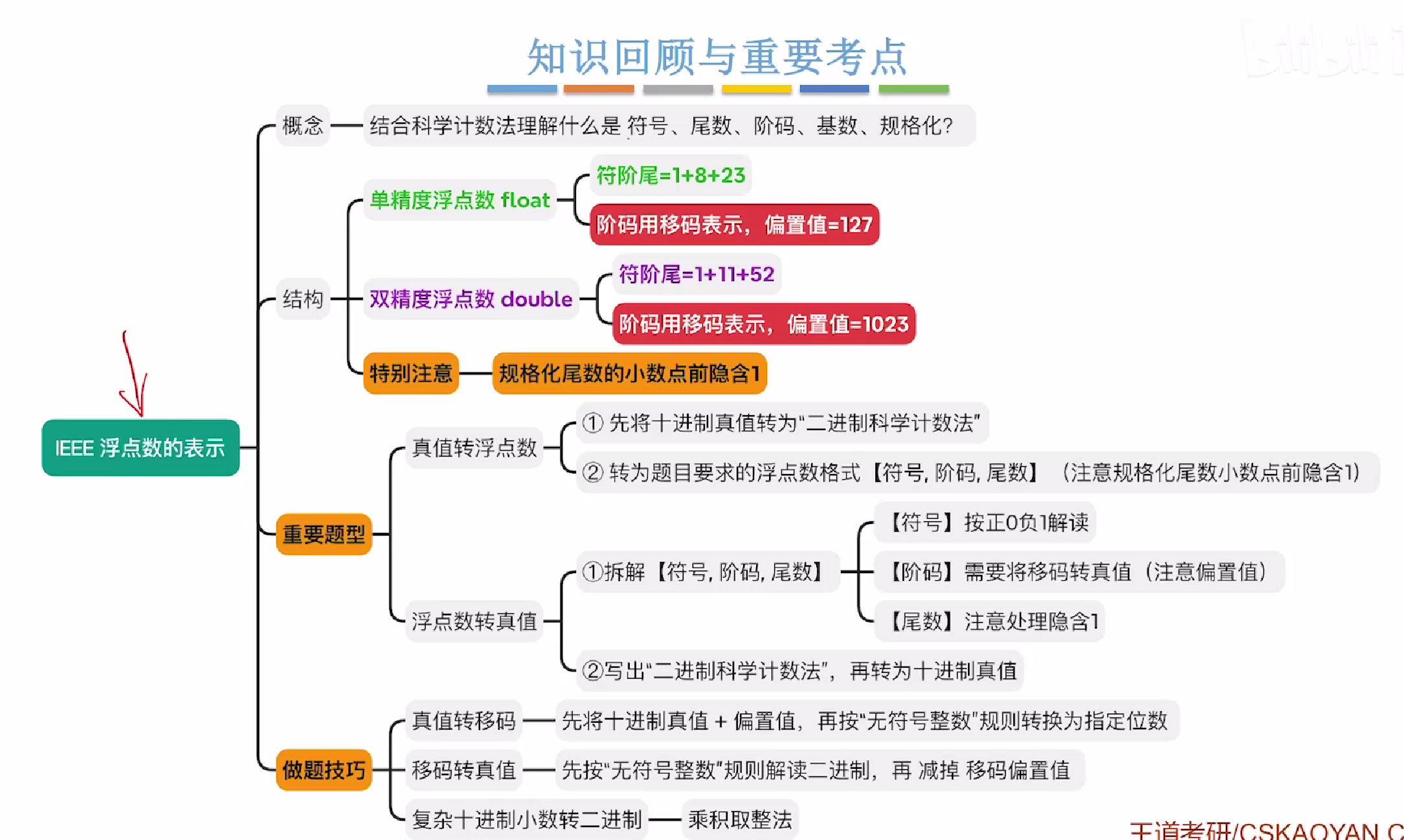
浮点数
主要主义的是单双精度的浮点数的表示方法
注意阶码的偏置值,用阶码-偏置值即可得到阶码的真值
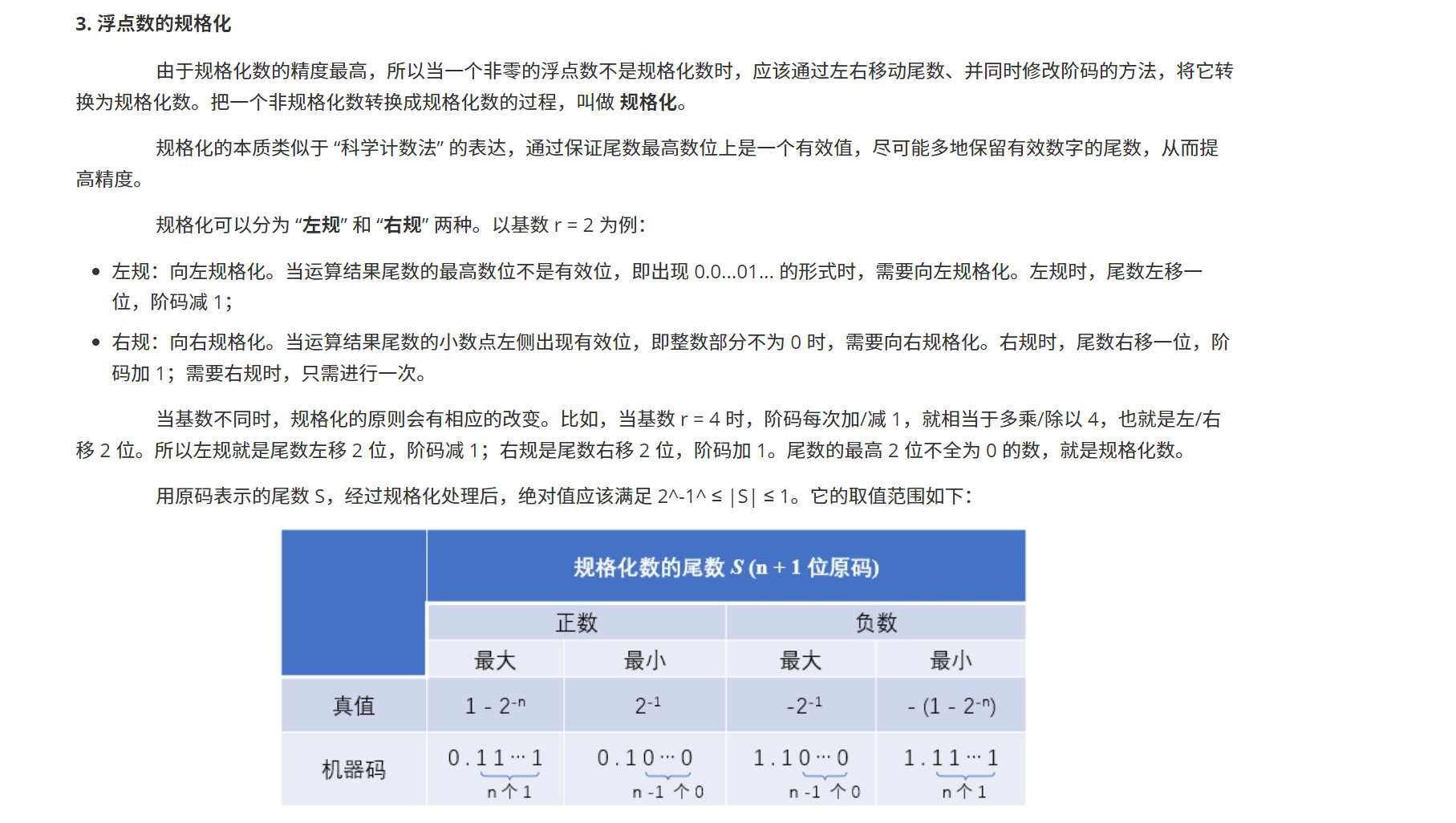
规格化浮点数及其真值表示范围
当为非IEEE 754标准的浮点数规格化,其本质就代表着尾数的最高位次为一个有效数位,不能再进行移动
比如以2为基数的规格化数
0.1111
这样的数字,其尾数的最高位为1,那么其为有效数位,在这种情况下,你往左移动一位,会溢出,往右移一位,会使得最高位不是有效位
那么这样的数被称为规格化
那么如果以4为基数的规格化数
其阶码加一,那么就代表着尾数需要移动两位才能抹平差距
所以,基数为4的规格化数进行左右规的时候,一次性需要移动两位数字
所以对于基数为4的规格化数
其规格化表现为
0.xx 1010100
xx处不为0,即一次左规会导致溢出,然后一次右规又会导致最高位无效,其尾数部分最高有效位为开头的两位数
若基数为8则是开头前三位不为0即可
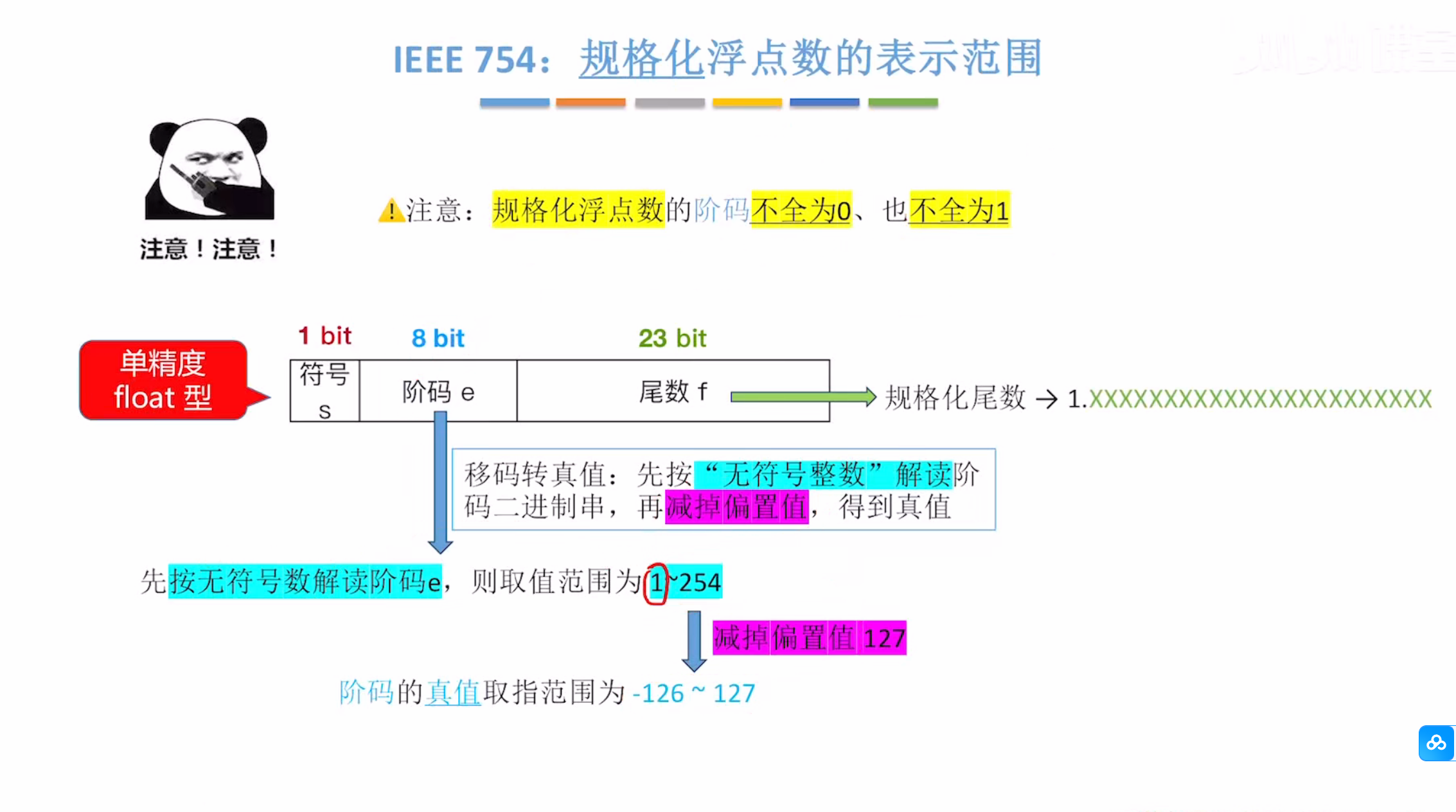
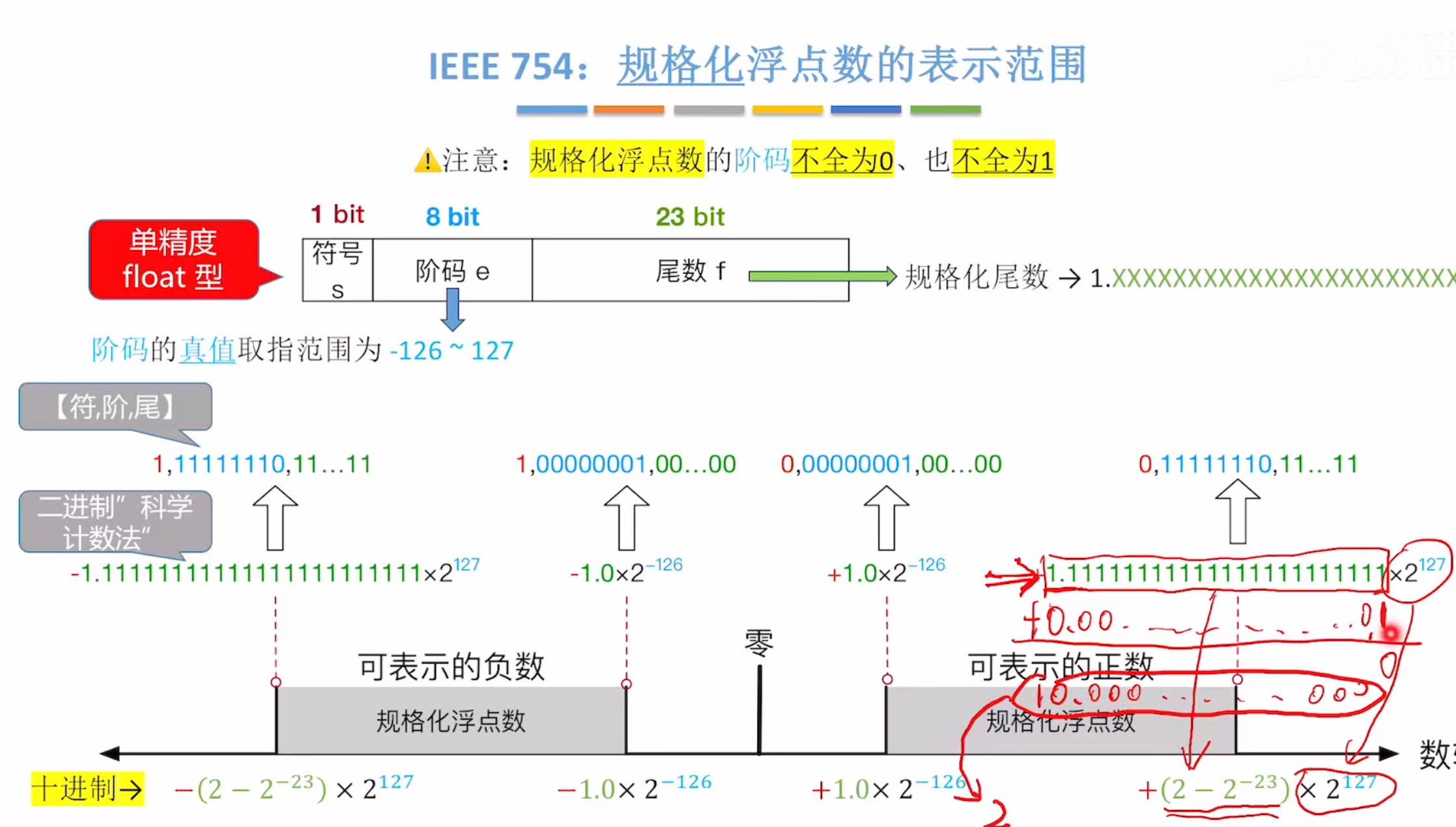
十进制表示法如图所示推导
特殊浮点数
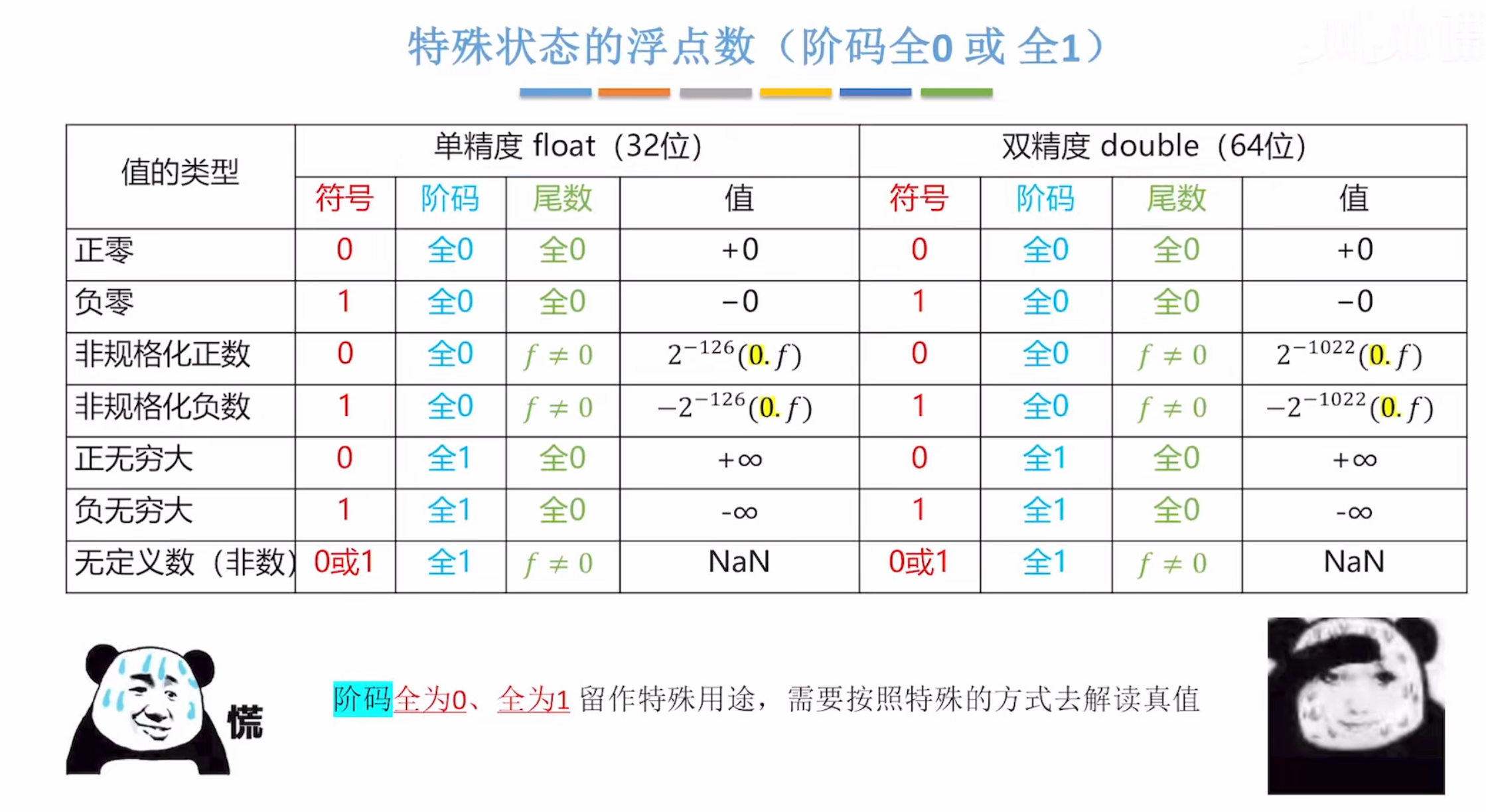
非规格化浮点数的表示及其范围
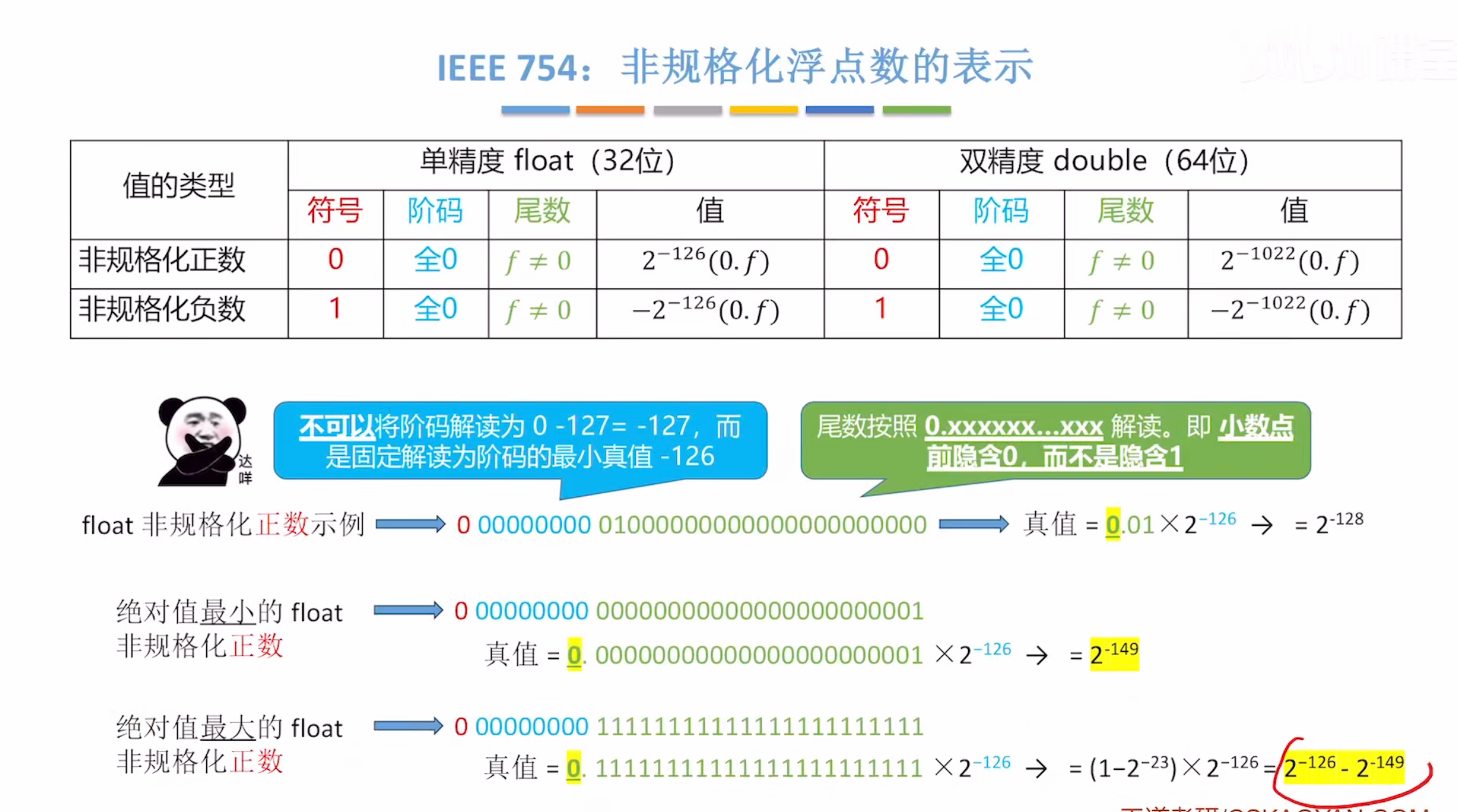
负数只需要添加负号即可

浮点数表示范围总结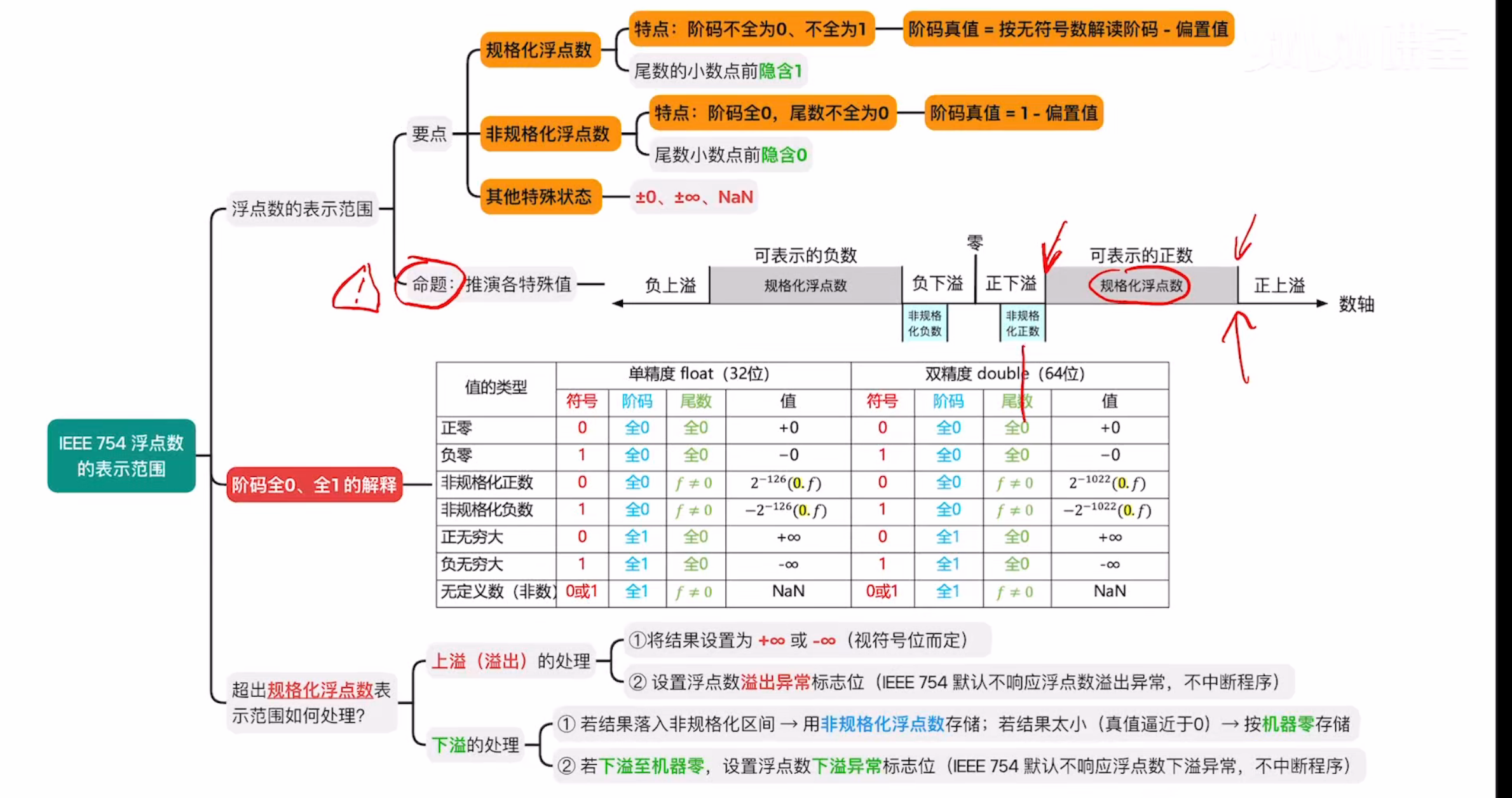
错题
答案:D
对阶操作中,浮点数的格式都是相同的,所以不会发生溢出
尾数舍入时,如右图所示,假定25位尾数舍入一个1然后进一,导致一直进位,然后需要右规,所以阶码变大可能上溢
尾数溢出时,我们只需要调整阶码即可

答案:B
这种类型的题目关键在于判断精度的转化是难点
比如int 型数据能够表示31位的数
float只能表示到24位
如图所示,如果int 表示了31位数的1
那么转换为浮点数,其规格化之后尾数部分有30个1此时尾数部分超出所以要舍弃则精度丢失

对于Ⅳ选项他有如下过程,列出两个数的数值大小,我们发现如果要进行计算那么f会进行强制类型转换然后进行对阶运算,其中发现阶码需要变大大约210,那么尾数需要右移210位,而double类型的尾数只能够表示53位所以f相当于后面的都被舍弃变成了0,这种现象叫做大数吃小数
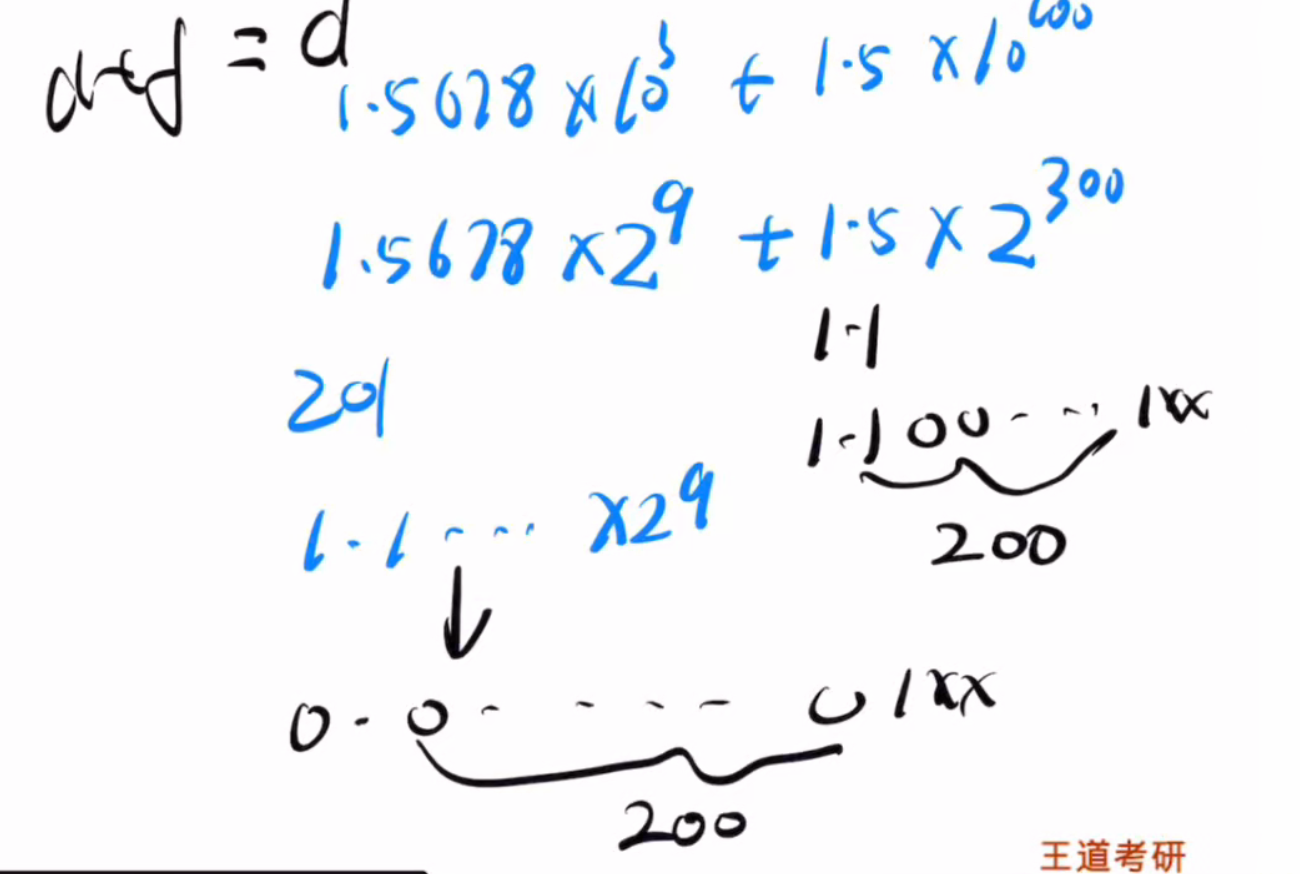
答案:D
解题步骤
A的尾数部分为
x: 00 111 00 11101
y:00 101 00 10100
此时发现y的阶码小于x
我们对y进行右规和阶码扩大
y: 00 111 00 00101
x: 00 111 00 11101
两者相加
得到00 111 01 00010
此时发现尾数部分符号位多出两位进行右规
同时阶码+1
得到 01 000 00 10001
此时我们发现阶码溢出
故选D

答案:D
c语言主要转型的机制如下


答案:B
可以根据下图所示的运算规则进行判断
但同时也可以直接用概念判断
cf表示无符号数是否溢出,所以我们直接将r1和r2进行无符号数相减判断是否溢出即可,r1>r2所以不会溢出cf=0
of代表有符号数是否溢出两个负数相减则肯定不会溢出
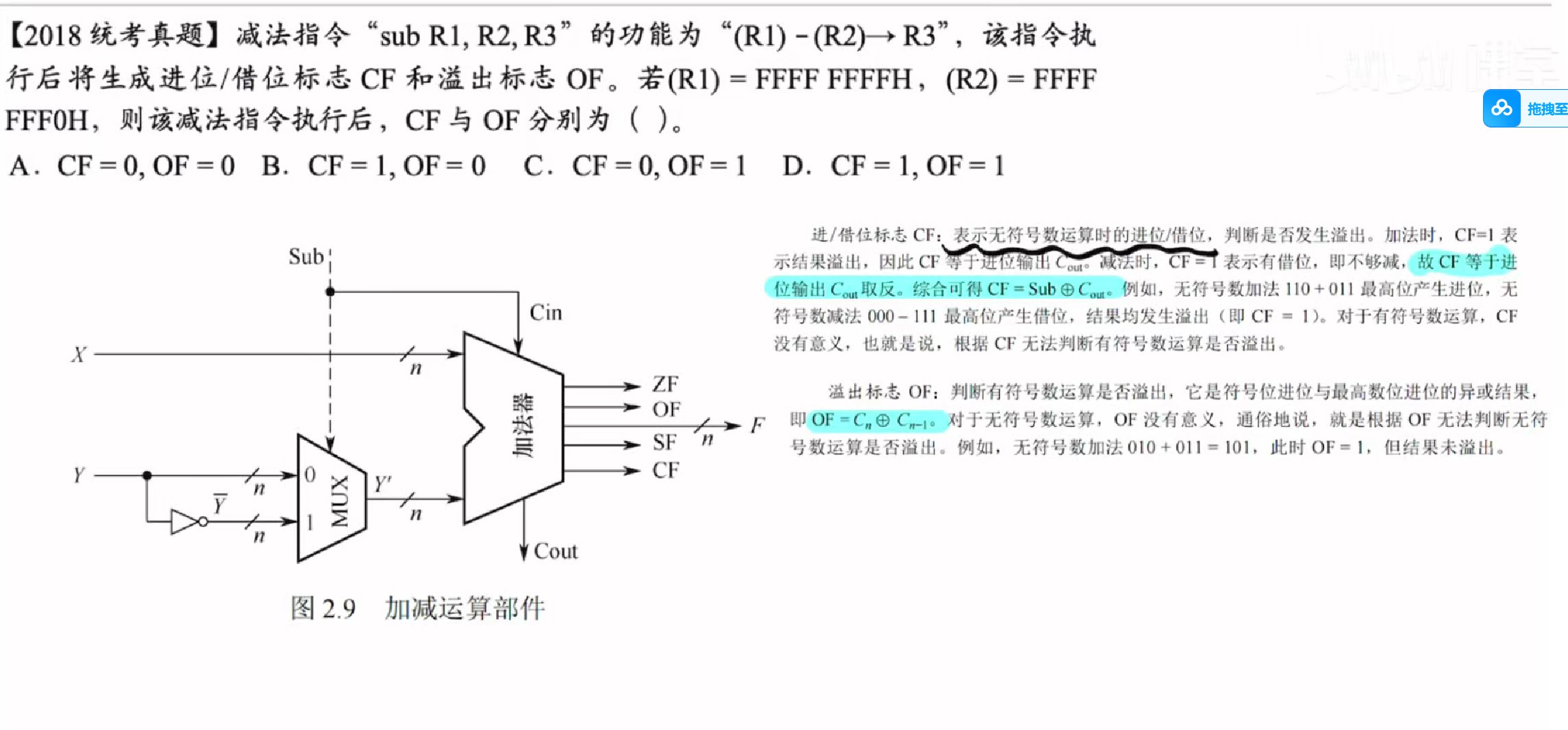
答案:A
cf代表无符号数的溢出
所以我们将-20进行无符号数的转换
int型32位二进制数
所以y=
x-y一定溢出无符号整数范围

本章重要记忆点
浮点数补码表示法
浮点数采用补码表示其符号位和尾数首位一定相反
移位运算
算数移位运算:用于移动有符号数,符号位也跟着移动,左移补零,右移补符号位,若移动后符号位发生改变则溢出
逻辑移位运算:直接补零
补码表示范围
对于一个n位补码表示的范围为[-2的n-1次方,2的n-1次方-1]
加减运算器及其CF OF标志位的判断

