机器人学和自动化领域中的路径规划方法

路径规划是机器人学和自动化领域中的一个重要问题，其目的是找到一条从起始点到目标点的路径，同时避免障碍物和满足特定的约束条件。以下是一些常见的路径规划方法：

1. 栅格法（Grid-based methods）：

   • 将环境划分为栅格单元，每个单元具有特定的状态（如自由、障碍物）。
   • 通过搜索算法（如Dijkstra算法、A*算法）在栅格上找到一条路径。

2. 人工势场法（Artificial Potential Fields）：

   • 使用吸引力和排斥力模拟机器人在环境中的移动。
   • 吸引力将机器人拉向目标点，排斥力将机器人从障碍物推开。

3. Dijkstra算法：

   • 一种经典的最短路径搜索算法，适用于加权图。
   • 从起始点开始，逐步扩展到相邻节点，直到到达目标点。

4. A*算法（A-Star）：

   • 是Dijkstra算法的改进，使用启发式函数来估计从当前节点到目标节点的距离。
   • 通过优先扩展估计距离最小的节点来加速搜索过程。

5. RRT（快速随机树）算法：

   • 一种概率性算法，通过随机采样快速生成路径。
   • 适用于高维空间和复杂环境。

6. PRM（概率路图）算法：

   • 通过在构型空间中随机采样生成图，然后找到一条连接起始点和目标点的路径。
   • 适用于高维空间和大规模问题。

7. 遗传算法（Genetic Algorithms）：

   • 模拟自然选择和遗传机制，通过迭代优化路径。
   • 适用于复杂的优化问题，但计算成本较高。

8. 粒子群优化（Particle Swarm Optimization, PSO）：

   • 模拟鸟群或鱼群的行为，通过群体协作找到最优路径。
   • 适用于连续空间的优化问题。

9. 动态窗口法（Dynamic Window Approach）：

   • 只考虑机器人当前位置周围的局部环境，动态地更新路径。
   • 适用于需要实时反应的环境，如移动机器人避障。

10. 模型预测控制（Model Predictive Control, MPC）：

    • 通过预测未来一段时间内的路径来优化当前的控制输入。
    • 适用于需要考虑动力学约束的路径规划问题。

每种方法都有其优缺点，适用于不同的应用场景。在实际应用中，可能需要根据具体问题的特点和约束条件选择合适的路径规划方法，或者将多种方法结合起来使用。

下面对其中一些方法进行详细讲解：
基于采样的路径规划算法是一类在构型空间或状态空间中通过随机采样来寻找路径的方法。这些算法特别适用于高维空间和复杂环境，因为它们不依赖于环境的网格化表示。以下是几种常见的基于采样的路径规划算法：

一：基于采样的规划算法

1. 快速随机树（Rapidly-exploring Random Tree, RRT）

原理：

• RRT是一种增量式算法，它通过随机采样并连接这些采样点来构建一棵树。
• 算法从起始点开始，随机选择一个目标点，然后找到树中离这个目标点最近的节点，并向目标点方向扩展。

特点：

• 易于实现，适用于高维空间。
• 不保证找到最优解，但通常能找到可行解。
• 对于非凸空间和障碍物较多的环境表现良好。

---

RRT伪代码:

---

$Algorithm1:RRTAlgorithm$
$Input:M,x_{init},x_{goal}$
$Result:Apath\Gamma from{x}_{init}to{x}_{goal}$
$T.init();$\\初始化空间树
$fori=1tondo$
$x_{rand}\leftarrow Sample(M);$ \\在关键空间中做一个随机采样
$x_{near}\leftarrow Near(x_{rand},T);$\\在树结构中找到一个距离$x_{rand}$最近的点$x_{near}$
$x_{new}\leftarrow Steer(x_{rand},x_{near},StepSize);$\\在最近的点$x_{near}$点附近找到另一个随机采样点x_{rand},并朝着$x_{rand}迈进一小步，大小为StepSize$
$E_i\leftarrow Edge(x_{new},x_{near});$ \\构建$x_{near}$到$x_{new}$的边
$ifCollisionFree(M,E_i)then$\\检测边$E_i$在关键空间中是否发生碰撞
$T.addNode(x_{new});$\\如果不发生碰撞，则把新点$x_{new}$加到空间树中
$T.addEdge(E_i);$\\把新边$E_i$也加到空间树中
$if{x}_{new}=x_{goal}then$\\直到新节点等于目标节点或者$dist|x_{new}-x_{goal}|<某个阈值$
$Success();$

---

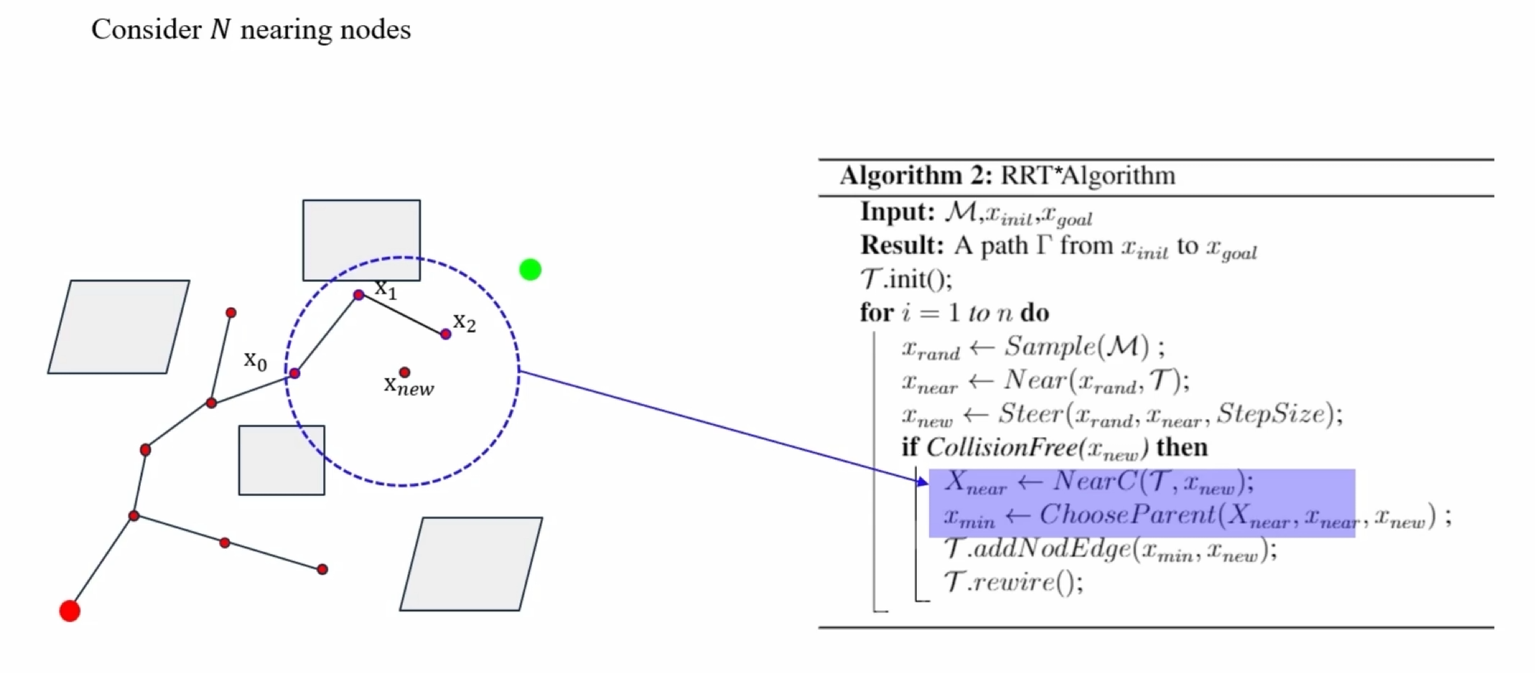
2. 快速随机树星（Rapidly-exploring Random Tree Star, RRT*）

原理：

• RRT*是RRT的改进版本，它不仅能够快速找到一条路径，还试图优化这条路径，使其尽可能短。
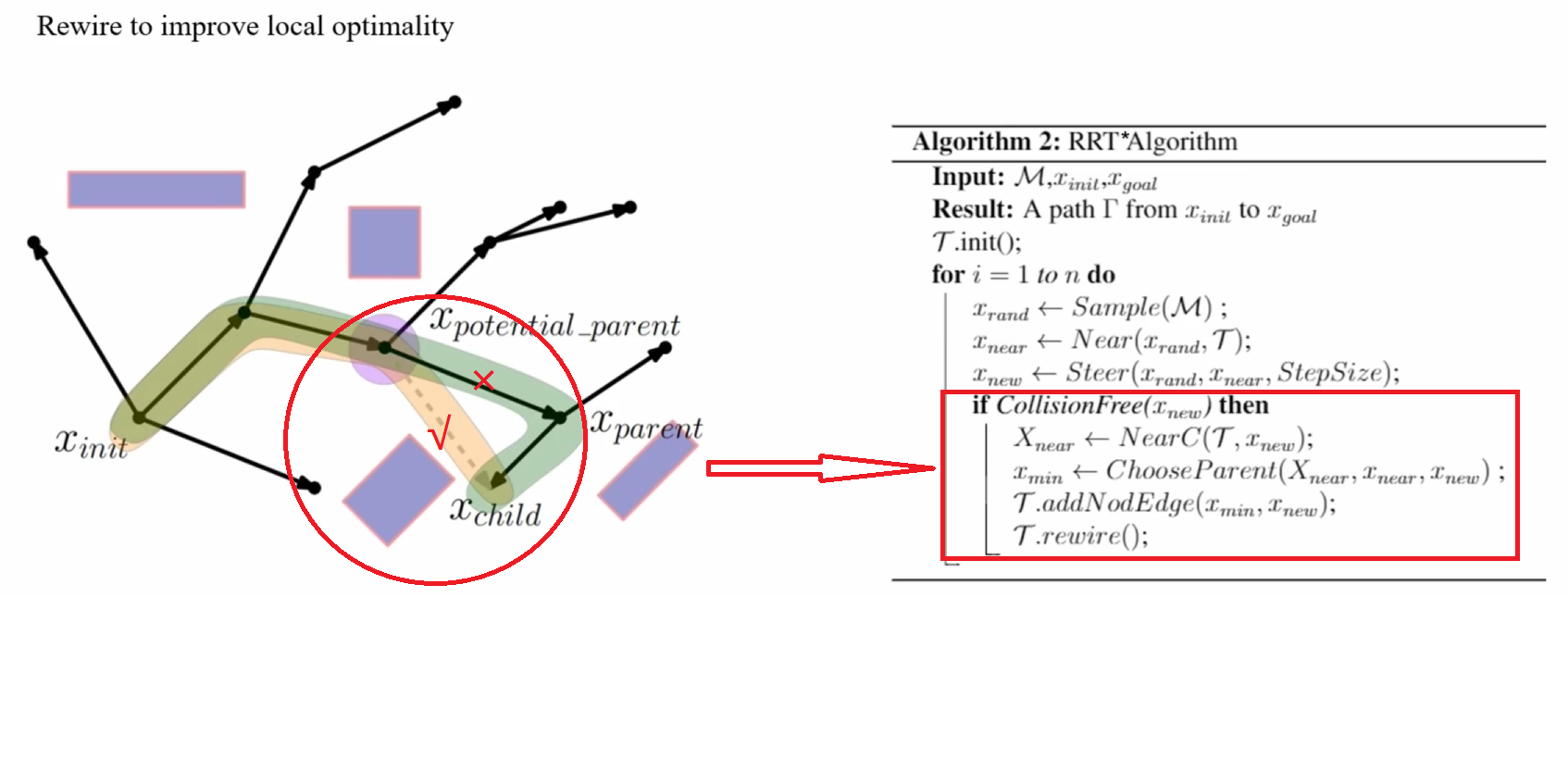
• 通过重新连接树中的边和节点，RRT*能够在找到路径后继续改进路径的质量。

特点：

• 渐近最优，即随着时间的推移，找到的路径会越来越接近最优路径。
• 计算成本比RRT高，因为需要更多的重新连接和优化步骤。
  
  

3. 概率路图（Probabilistic Roadmap, PRM）

原理：

• PRM首先在构型空间中随机采样大量点，然后连接这些点以形成图。
• 一旦图构建完成，就可以使用图搜索算法（如A*）找到从起始点到目标点的路径。

特点：

• 适用于静态环境，因为一旦构建了图，环境就被假定为不变。
• 对于高维空间表现良好，因为采样点的数量通常与维度无关。
• 需要足够的采样密度以确保图的连通性。

4. 基于采样的优化算法

原理：

• 这些算法（如基于采样的优化算法SBO）通过在路径上随机采样并优化这些采样点来改进路径。
• 通过迭代优化，可以找到更平滑、更短或更符合特定约束的路径。

特点：

• 可以结合RRT、PRM等算法使用，以提高路径的质量。
• 适用于需要优化路径平滑性或能量消耗的场景。

实现步骤

1. 采样：在构型空间或状态空间中随机采样点。
2. 连接：根据某种规则（如距离）连接采样点，形成树或图。
3. 搜索：使用图搜索算法找到从起始点到目标点的路径。
4. 优化（可选）：通过迭代优化路径上的点来改进路径。

基于采样的路径规划算法因其灵活性和对高维空间的适应性而受到广泛关注。然而，这些算法的性能很大程度上依赖于采样策略和环境的特性，因此在实际应用中需要仔细调整参数。

二：基于图结构的规划算法

1. Dijkstra算法：
   • 一种经典的最短路径搜索算法，适用于加权图。
   • 从起始点开始，逐步扩展到相邻节点，直到到达目标点。
     详情可参考我的另一篇博客，有对该算法有更加详细的介绍：
     Dijkstra算法一种用于求解单源最短路径问题的经典算法
2. A*算法（A-Star）：
   • 是Dijkstra算法的改进，使用启发式函数来估计从当前节点到目标节点的距离。
   • 通过优先扩展估计距离最小的节点来加速搜索过程。