ndarray的创建(小白五分钟从入门到精通)
ndarray的创建
用途 | 方法 | 语法示例 | 核心作用 | 输出示例 |
基础构造 | ||||
▪ 从 Python 数据结构创建 | np.array() | np.array([[1, 2], [3, 4]]) | 将列表/元组转换为 ndarray | array([[1, 2], [3, 4]]) |
▪ 复制数组 | np.copy() | np.copy(arr) | 创建独立副本(深拷贝) | 与原数组相同但不共享内存 |
预定义形状填充 | ||||
▪ 全0数组 | np.zeros() | np.zeros((2,3)) | 快速初始化全0数组 | [[0., 0., 0.], [0., 0., 0.]] |
▪ 全1数组 | np.ones() | np.ones((3,2), dtype=int) | 快速初始化全1数组 | [[1, 1], [1, 1], [1, 1]] |
▪ 未初始化数组 | np.empty() | np.empty((2,2)) | 预分配内存(值随机) | 随机值(如 [[1e-323, 0.], [0., 0.]]) |
▪ 填充固定值 | np.full() | np.full((2,3), 5) | 用指定值填充数组 | [[5, 5, 5], [5, 5, 5]] |
基于数值范围生成 | ||||
▪ 等差序列 | np.arange() | np.arange(0, 10, 2) | 生成步长固定的序列(不含终点) | [0, 2, 4, 6, 8] |
▪ 等间隔序列 | np.linspace() | np.linspace(0, 1, 5) | 生成指定数量的等间隔值(含终点) | [0.0, 0.25, 0.5, 0.75, 1.0] |
▪ 对数间隔序列 | np.logspace() | np.logspace(0, 2, 3, base=10) | 生成对数间隔值(如 10^0, 10^1, 10^2) | [1.0, 10.0, 100.0] |
特殊矩阵生成 | ||||
▪ 单位矩阵 | np.eye() | np.eye(3) | 生成单位矩阵(对角线为1) | [[1., 0., 0.], [0., 1., 0.], [0., 0., 1.]] |
▪ 对角矩阵 | np.diag() | np.diag([1, 2, 3]) | 生成以指定值为对角线的矩阵 | [[1, 0, 0], [0, 2, 0], [0, 0, 3]] |
随机数组生成 | ||||
▪ 均匀分布随机数 | np.random.rand() | np.random.rand(2,2) | 生成 [0,1) 均匀分布的随机数 | [[0.43, 0.89], [0.21, 0.57]] |
▪ 正态分布随机数 | np.random.randn() | np.random.randn(2,2) | 生成标准正态分布随机数(均值为0,方差为1) | [[-0.5, 1.2], [0.3, -1.8]] |
▪ 随机整数 | np.random.randint() | np.random.randint(1,10, (2,2)) | 生成指定范围内的随机整数 | [[3, 7], [5, 2]] |
高级构造方法 | ||||
▪ 从字符串创建 | np.array() | np.array(['a', 'bc']) | 将字符串转换为字符数组 | array(['a', 'bc'], dtype='<U2') |
▪ 从文件读取 | np.loadtxt() | np.loadtxt('data.txt') | 从文本文件加载数据 | 依赖文件内容(如 [[1., 2.], [3., 4.]]) |
▪ 函数生成数组 | np.fromfunction() | np.fromfunction(lambda i,j: i+j, (3,3)) | 根据函数生成数组元素 | [[0., 1., 2.], [1., 2., 3.], [2., 3., 4.]] |
创建方法汇总
- 基础构造: 适用于手动构建小规模数组或复制已有数据。
- 预定义形状填充: 用于快速初始化固定形状的数组(如全0占位、全1初始化)。
- 基于数值范围生成: 生成数值序列,常用于模拟时间序列、坐标网格等。
- 特殊矩阵生成: 数学运算专用(如线性代数中的单位矩阵)。
- 随机数组生成: 模拟实验数据、初始化神经网络权重等场景。
- 高级构造方法: 处理非结构化数据(如文件、字符串)或通过函数生成复杂数组。
2.2.3.1 从 Python 数据结构转换
将 Python 列表、元组等转换为 ndarray,是最直接的方式。
np.array(object, dtype=None)
Python |
注意事项
- 混合类型时,NumPy 会统一为最高优先级类型(如 int + float → float,数值 + 字符串 → 字符串)。
- 列表的嵌套层级决定 ndim(维度数)。
2.2.3.2 预定义形状填充
快速初始化固定形状的数组,常用于占位或初始化权重矩阵。
Python |
Python |
默认数据类型为 float64,需显式指定 dtype 为 int 或其他类型。
未初始化的数组 (np.empty)
np.empty(shape, dtype=float)
返回给定形状和类型的未初始化的新数组。
创建未初始化的数组(值随机,取决于内存状态),适用于对性能要求极高的场景。
Python |
不推荐直接使用:需手动填充数据,否则可能引入不可预测的错误。
需要注意的是,np.empty 并不保证数组元素被初始化为 0,它只是分配内存空间,数组中的元素值是未初始化的,可能是内存中的任意值。
重复填充数组 (np.full)
np.full(shape, fill_value, dtype)
Python |
zeros_like():返回与给定数组具有相同形状和类型的0新数组。
ones_like():返回与给定数组具有相同形状和类型的1新数组。
empty_like():返回与给定数组具有相同形状和类型的未初始化的新数组。
Plain Text |
2.2.3.3 基于数值范围生成
(1) np.arange:等差序列
np.arange(start, stop, step)
返回在给定范围内用均匀间隔的值填充的一维数组。
Python |
(2) np.linspace:等间隔数组(含终点)
np.linspace(start, stop, num=50)
返回指定范围和元素个数的等差数列。数组元素类型为浮点型。
Python |
(3) np.logspace:对数间隔数组
np.logspace(start, stop, num=50, base=10)
返回指定指数范围、元素个数、底数的等比数列。
Python |
2.2.3.4 特殊矩阵
矩阵补充知识
矩阵是线性代数的核心概念,可以理解为一个数字的矩形表格,用来表示数据、方程组或线性变换。下面用最直观的方式介绍它的基本概念和应用。
矩阵是一个由 行(row) 和 列(column) 排列成的矩形数组,例如:
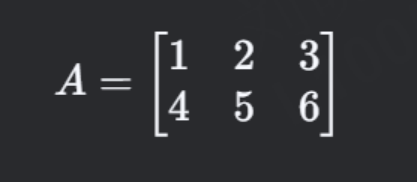
- 形状(shape):这个矩阵有 2 行 3 列,记作 2×32×3 矩阵。
- 元素(entry):矩阵中的每个数字称为元素,如 A1,2=2A1,2=2(第 1 行第 2 列)。
- 矩阵的用途
(1) 表示线性方程组
例如,方程组:
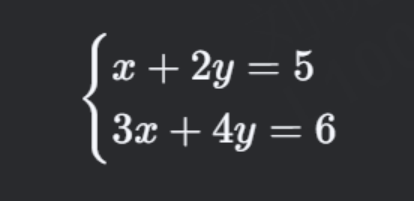
可以写成矩阵形式:
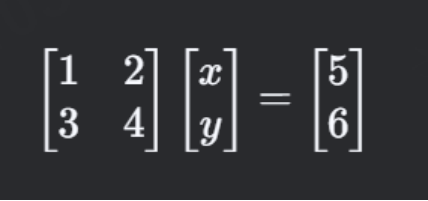
即 Ax=b,其中:
- A 是系数矩阵,
- x 是未知数列向量,
- b 是常数项列向量。
(2) 表示线性变换
矩阵可以描述空间中的变换,比如旋转、缩放、投影。
例如,一个 2×22×2 矩阵可以表示二维平面的旋转:
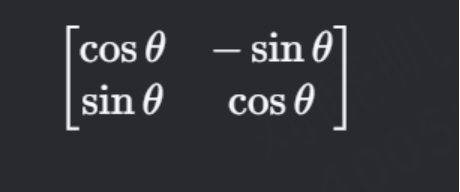
作用在向量 [xy][xy] 上,会使其旋转 θθ 角度。
(3) 数据表示(如机器学习)
在机器学习中,数据集通常用矩阵表示:
- 每一行代表一个样本(如一张图片),
- 每一列代表一个特征(如像素值)。
- 矩阵的基本运算
(1) 矩阵加法
对应位置的元素相加,要求两个矩阵形状相同:
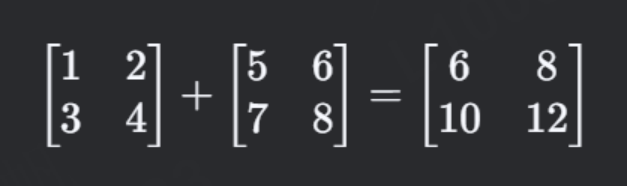
(2) 矩阵数乘
矩阵的每个元素乘以一个标量(数):
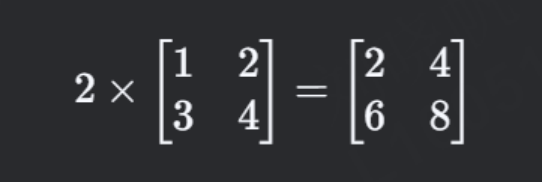
(3) 矩阵乘法
矩阵乘法 不是 对应元素相乘,而是 行 × 列 的点积运算:

注意:矩阵乘法不满足交换律(AB≠BAAB=BA)。
(4) 转置(Transpose)
行列互换:

- 特殊矩阵
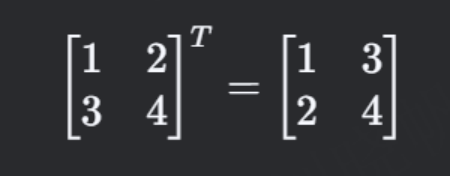
(1) 单位矩阵 (np.eye/np.identity)
Python |
Python |
(2) 对角矩阵 (np.diag)
Python |
Python |
2.2.3.5 随机数组
(1) 均匀分布随机数 (np.random.rand)
返回给定形状的数组,用 [0, 1) 上均匀分布的随机样本填充。
Python |
(2) 正态分布随机数 (np.random.randn)
返回给定形状的数组,用标准正态分布(均值为0,标准差为1)的随机样本填充。
Python |
(3) 随机整数 (np.random.randint)
返回给定形状的数组,用从低位(包含)到高位(不包含)上均匀分布的随机整数填充。
Python |
(4)random.uniform()
random.uniform():返回给定形状的数组,用从低位(包含)到高位(不包含)上均匀分布的随机浮点数填充。
arr3 = np.random.uniform(3, 6, (2, 3))
# [[5.69275495 3.84857937 3.2899215 ]
# [5.32035519 3.7460973 3.33859905]]
(5) 设置随机种子 (np.random.seed)
np.random.seed 是 NumPy 中用于设置**随机数生成器种子**的函数,目的是确保程序的随机操作可以重复生成相同的结果(即保证随机结果的确定性)。这在实验复现、调试和教学场景中非常有用。
Python |
每次运行上述代码都会得到相同的随机数序列(例如 [0.37454012, 0.95071431, 0.73199394])。
关键细节
- 种子的一致性:
- 相同种子生成的随机数序列完全一致。
- 不同种子(如 np.random.seed(0) 和 np.random.seed(1))会产生不同序列。
- 作用范围:
- 种子对后续所有基于 NumPy 的随机函数生效(如 np.random.rand(), np.random.normal(), np.random.shuffle() 等)。
通过控制种子,你能在“随机”和“可复现”之间灵活切换!
2.2.3.6 高级构造方法
(1) np.loadtxt
Python |
(2) np.genfromtxt
Python |
2.2.3.7 创建方法推荐场景
场景 | 推荐方法 | 优点 |
快速初始化全0/全1数组 | np.zeros/np.ones | 内存预分配,明确值 |
生成数值序列 | np.arange/np.linspace | 灵活控制范围和步长 |
创建单位矩阵或对角矩阵 | np.eye/np.diag | 数学运算专用 |
高性能预分配内存 | np.empty | 速度最快(需手动初始化) |
随机数据生成 | np.random 模块 | 模拟实验数据 |
