复变函数中的对数函数及其MATLAB演示
复变函数中的对数函数及其MATLAB演示
引言
在实变函数中,对数函数 ln x \ln x lnx定义在正实数集上,是一个相对简单的概念。然而,当我们进入复变函数领域时,对数函数展现出更加丰富和复杂的性质。本文将介绍复变函数中对数函数的基本概念、性质,并通过MATLAB进行可视化演示。
复对数函数的定义
复对数函数是实对数函数的推广。对于非零复数 z z z,其对数定义为:
ln z = ln ∣ z ∣ + i ( Arg ( z ) + 2 π k ) , k ∈ Z \ln z = \ln|z| + i(\operatorname{Arg}(z) + 2\pi k),\quad k \in \mathbb{Z} lnz=ln∣z∣+i(Arg(z)+2πk),k∈Z
这里:
- ∣ z ∣ |z| ∣z∣是 z z z的模
- Arg ( z ) \operatorname{Arg}(z) Arg(z)是 z z z的主辐角(通常取 ( − π , π ] (-\pi, \pi] (−π,π])
- k k k为任意整数,表明复对数是一个多值函数
主值(当 k = 0 k=0 k=0时)记为:
Ln z = ln ∣ z ∣ + i Arg ( z ) \operatorname{Ln} z = \ln|z| + i\operatorname{Arg}(z) Lnz=ln∣z∣+iArg(z)
复对数的性质
- 多值性:复对数函数有无穷多个值,各值相差 2 π i 2\pi i 2πi的整数倍
MATLAB演示
计算复对数:
MATLAB中使用log函数计算复对数的主值:
z = 1 + 1i;
ln_z = log(z);
disp(['主值: ', num2str(ln_z)]);
disp(['实部(ln|z|): ', num2str(real(ln_z))]);
disp(['虚部(Arg(z)): ', num2str(imag(ln_z))]);
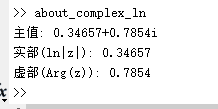
运行结果:
结论
Matlab中log函数可以直接计算复数的主值
