手搓传染病模型（SEIAR）

在探寻传染病传播规律与趋势预测的众多模型中，SEIAR 模型占据着独特地位，它特别适用于描绘那些具有特定特性的急性传染病流行走向。这类疾病往往具备传染性强、传播途径直接且简单、存在隐性感染者、潜伏期较短、感染后一段时间内具备传染性、病程整体较短、在治愈过程中不提供免疫保护等特点。SEIAR 模型中，各个字母分别对应不同人群：S 代表易感者，E 代表暴露者，I 代表显性感染者，A 代表隐性感染者，R 代表康复者。在模型动态运行中，S 仓室会以单位时间 betaS(I + κA) 的速率向 E 仓室流入，而 E 仓室同样以单位时间 betaS(I + κA) 的速率向 E 仓室流入。

先看模型

话不多说咱们开始手搓

% 模型参数
N = 10000; % 总人数
I0 = 10; % 初始有症状感染人数
p = 0.15; % 发病概率
A0 = I0 * p / (1 - p); % 初始无症状感染人数
E0 = I0 * 2; % 初始暴露人数
R0 = 0; % 初始康复人数
S0 = N - I0 - A0 - E0; % 初始易感人数
beta = 0.001; % 传染率
omega1 = 0.5; % 暴露转化为感染者速率
omega2 = 0.8; % 暴露转化为无症状感染者速率
kappa = 0.5; % 隐形感染者相对患者的传染力的倍数
gamma1 = 0.2; % 显性感染者康复率
gamma2 = 0.25; % 无症状感染者康复率
epsilon = 0.0027; % 恢复者失去免疫力的速率
num_days = 50; % 模拟天数% x(1):有症状感染人群I， 
% x(2):易感人群S， 
% x(3):无症状感染人群A，
% x(4):暴露人群E
% x(5):康复人群R
dxdt = @(t, x) [(1 - p) * omega1 * x(4) - gamma1 * x(1); % dIdt-beta * x(2) * (x(1) + x(3) * kappa) / N + epsilon * x(5); % dSdtp * omega2 * x(4) - gamma2 * x(3); % dAdtbeta * x(2) * (x(1) + x(3) * kappa) / N - (p * omega1 + (1 - p) * omega2) * x(4); % dEdtgamma1 * x(1) + gamma2 * x(3) - epsilon * x(5) % dRdt];[t, y] = ode45(dxdt, 1: num_days, [I0, S0, A0, E0, R0]);
hold on
plot(t, y(:, 1));
% plot(t, y(:, 2));
plot(t, y(:, 3));
plot(t, y(:, 4));
plot(t, y(:, 5));
legend('感染人数I', '无症状感染人群A', '暴露人群E', '康复人群R', 'Location', 'best');

看下效果

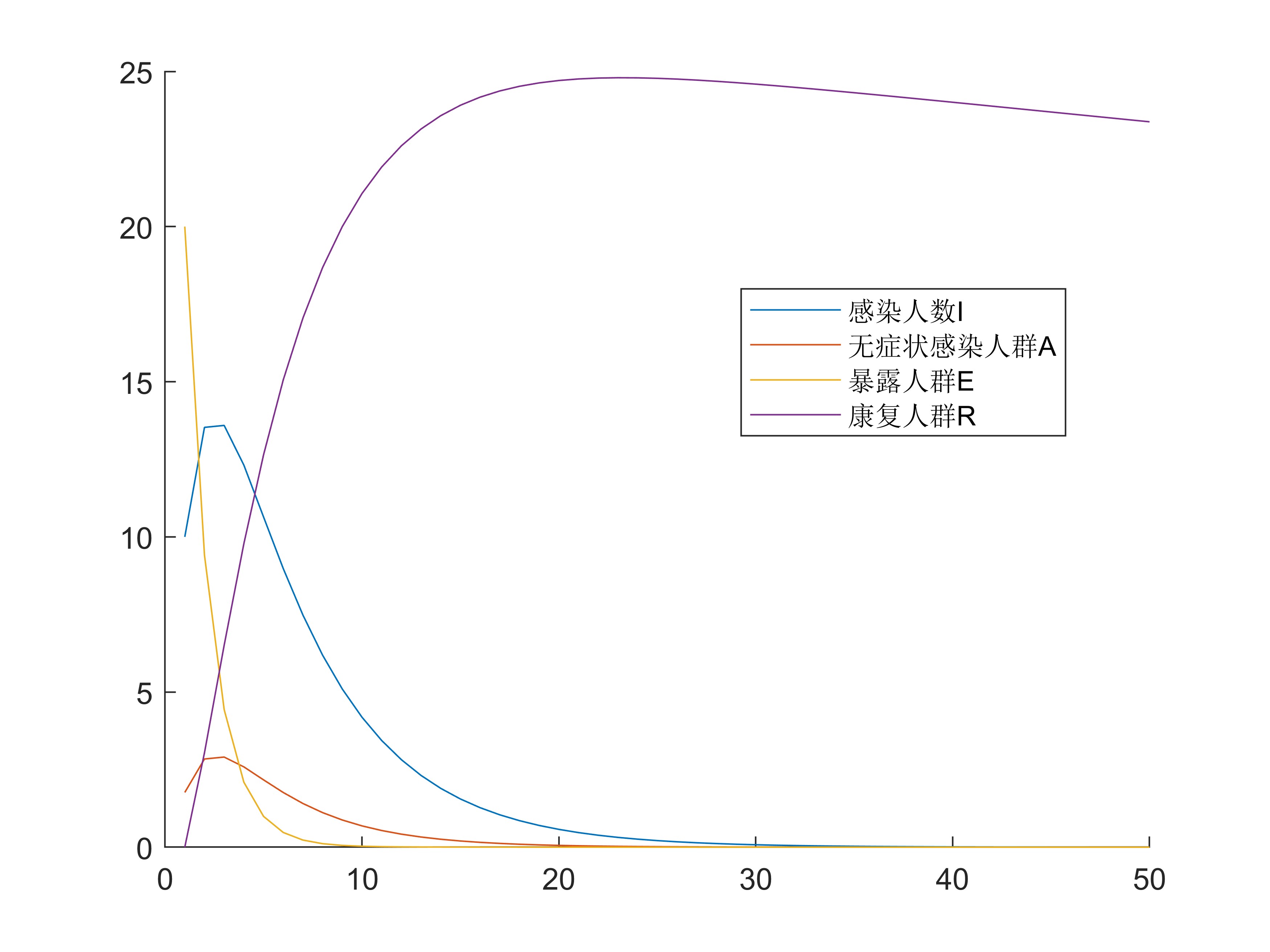
结果解读

在模拟小区或学校流感疫情的 SEIAR 模型中，我们观察到疫情的阶段性发展态势呈现出一种此起彼伏的波浪式态势。初始阶段，虽仅10人感染，但随着病毒迅速传播，暴露者（E）人数在第0天达到20人，成为疫情的“前哨”。随后，显性感染者（I）与无症状感染者（A）在第2天同步达到峰值（分别为14人与3人），标志着感染的势头迅猛。随着疫情的持续，康复者（R）人数在第22天达到25人，预示着群体免疫屏障的初步形成。整个疫情进程在第3天迎来新增感染高峰，而至第30天，新增感染人数逐渐归零，呈现出疫情从爆发到平息的完整周期特性。这一动态过程揭示了流感在封闭社区传播的阶段性特征，为制定精准防控策略提供了理论依据。