RL代码实践 02——策略迭代
目录
一、问题描述
二、问题分析和解决
1、策略迭代算法
一、问题描述
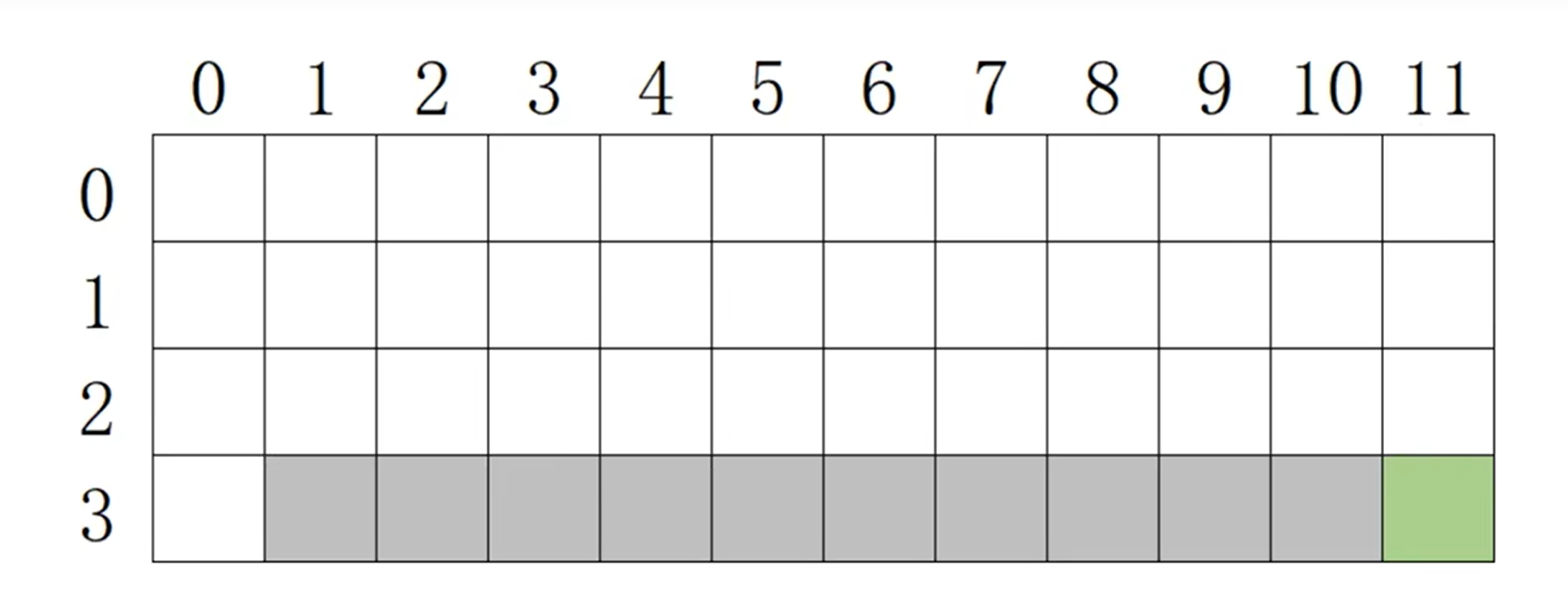
悬崖漫步
灰色格子代表悬崖,一旦进入就游戏失败;
绿色格子是终点,一旦进入就游戏成功;
白色格子是通路。
已知对于每个格子,可选的动作有4种,分别往上下左右走。
奖惩规则如下:
- 普通步长:
-1(鼓励少走步)- 撞墙:
-2(略高于普通步长,减少撞墙)- 终点:
+50,悬崖陷阱:-100(明确目标和风险)求每个格子的策略,使可以找到通往终点的最优路径。
二、问题分析和解决
这是一个有模型的情况:
对于特定的状态(格子)s,采取特定的动作a后,能到达的下一状态已知且概率已知,
获得的奖励已知且概率已知。
可以用策略迭代算法或者值迭代算法。
1、策略迭代算法
首先初始化策略,主要分为两个阶段:
(1)策略评估(Policy Evaluation)
需要计算出各个状态的value。
有两个方法:一个是根据贝尔曼公式求解,另一个是用迭代求解。
这里用迭代算法求解,直到value收敛(np.abs(values - old_values) < theta))才结束。
具体来说,
即对于第k轮迭代,
某状态的 state value = 各个动作的q值 * 各个动作的概率 之和,
而q值 action value = reward + next_state_value * 0.9。
注意此时next_state_value是上一轮,即k-1轮的值。
(2)策略改进(Policy Improvement)
get_pi()使用贪心策略(np.argmax)选择每个状态的最优动作,生成确定性策略(概率1赋予最优动作)。也可以采用用随机性策略:若多个动作的 Q 值相同,可均分概率。(但是值迭代算法一般默认greedy,不用随机性策略)
外层循环交替执行策略评估和策略改进,直到策略稳定(pi == old_pi)。
# 悬崖漫步
import numpy as np# 设置(获取)格子状态
def get_state(row, col):if row!=3 or col==0:return 'ground' # 通路if row==3 and col==11:return 'terminal' # 终点return 'trap' # 悬崖for row in range(4):for col in range(12):if get_state(row, col)=='ground':print('o', end=' ') # 不换行,用空字符结尾elif get_state(row,col)=='terminal':print('p', end=' ')else:print('x', end=' ')print()# 在特定s做特定a,求得到的下一s和r
def move(row, col, action):# 如果当前状态已经是掉进悬崖或者到达终点,直接返回(因为游戏结束了,不会再有状态转移)if get_state(row,col) in ['terminal', 'trap']:return row, col, 0 # 让它待在原地不能移动,原地不动没有奖惩# 状态转移if action == 0: # 向上走row-=1elif action == 1: # 向下走row+=1elif action == 2: # 向左走col-=1elif action == 3: # 向右走col+=1# 注意限制不能走出地图外面去out = 0 # 标记是否出界if row<0 or row>3 or col<0 or col>11:out = 1row = max(0,row)row = min(3,row)col = max(0,col)col = min(11,col)# 获得奖励reward = -1 # 普通步长if get_state(row, col)=='trap':reward = -100 # 陷阱if get_state(row, col)=='terminal':reward = 50 # 终点if out==1:reward = -2 # 出界(撞墙)return row, col, reward# 初始化state value table
values = np.zeros((4,12))
# 初始化q-table
q_table = np.zeros((4,12,4))
# 初始化策略(每个格子下采取动作的概率)
pi = np.ones((4,12,4))*0.25# 计算q
def get_q(row, col, action):# 当前rewardnext_row, next_col, reward = move(row, col, action)# 下一状态的valuenext_state_value = values[next_row, next_col]# s,a对应的action valuereturn reward + next_state_value * 0.9# 计算q-table(选择所有动作的可能性)
def get_q_table():new_q_table = np.zeros((4,12,4))# 遍历所有格子for row in range(4):for col in range(12):# 对于特定格子(状态),四个动作的q值for action in range(4):new_q_table[row, col, action] = get_q(row, col, action)return new_q_table# policy evaluation(value update)
def get_values():new_values = np.zeros((4,12))# 遍历所有格子for row in range(4):for col in range(12):# 终止状态价值为0if get_state(row, col) in ['terminal', 'trap']:new_values[row, col] = 0else:# 该状态的value = 各个动作的q值 * 各个动作的概率 之和new_values[row,col] = np.sum(q_table[row, col] * pi[row, col])return new_values# policy improvement(policy update)
def get_pi():new_pi = np.zeros((4,12,4))# 遍历所有格子for row in range(4):for col in range(12):# 终止状态无需策略if get_state(row, col) in ['terminal', 'trap']:continue# # 该状态下,有最大q值的动作有几个# max_q = np.max(q_table[row,col])# count = np.sum(q_table[row,col]==max_q)# # 让这些动作均分概率,其它为0# for action in range(4):# if q_table[row,col,action]==max_q:# new_pi[row, col, action]=1/count# else:# new_pi[row, col, action] =0# greedya = np.argmax(q_table[row, col])for action in range(4):if action == a:new_pi[row, col, action] = 1else:new_pi[row, col, action] = 0return new_pi# 循环迭代策略评估和策略提升,寻找最优解
# 增加收敛判断,可提前终止
theta = 1e-6 # 收敛阈值
for _ in range(100):old_pi = pi.copy() # 保存旧策略old_values = values.copy()# 策略评估:直到价值函数收敛while True:q_table = get_q_table()values = get_values()if np.all(np.abs(values - old_values) < theta):break # 价值函数收敛,结束本轮评估old_values = values.copy() # 注意:要更新旧价值,继续迭代# 策略提升:生成新策略pi = get_pi()if np.all(pi == old_pi):break # 策略不再变化时终止# 打印结果
for row in range(4):for col in range(12):state = get_state(row,col)if state == 'terminal':print('🚩', end=' ') # 终点elif state == 'trap':print('🪨', end=' ') # 悬崖else:action = np.argmax(pi[row, col])if action == 0:print('⬆️',end=' ')elif action == 1:print('⬇️', end=' ')elif action == 2:print('👈',end=' ')else:print('👉',end=' ')print()注意:
如果当前状态已经是掉进悬崖或者到达终点(终止状态),
则在状态转移move函数中,直接返回原地状态和reward=0(因为游戏结束了,不会再有状态转移,让它待在原地不动,没有奖惩);
在get_value函数中,终止状态的value为0(因为后续一直待在原地,奖惩一直为0);
在get_pi函数中,终止状态无需策略,后面打印时打印陷阱或终点的图标即可。

