数据结构day06

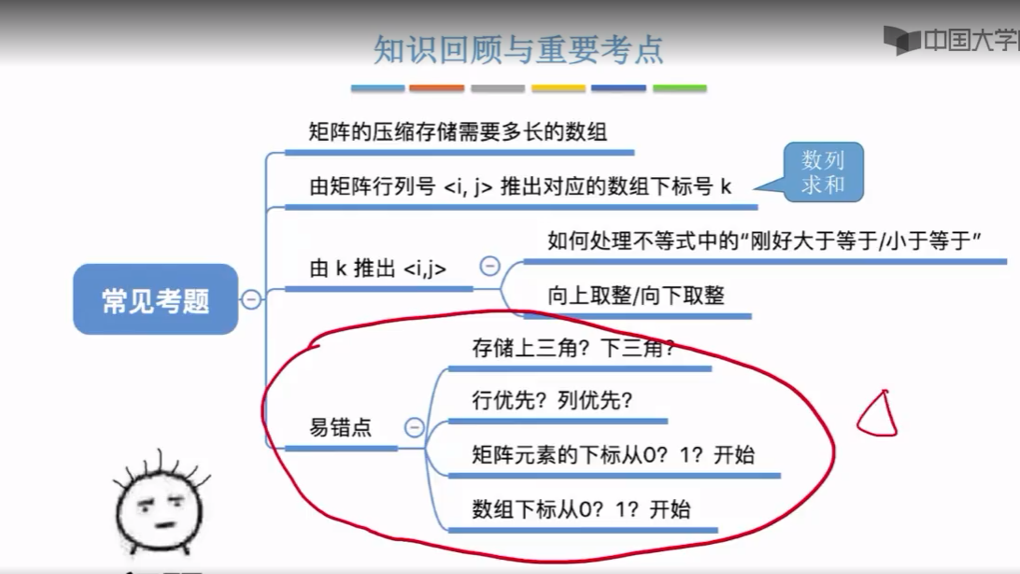
一 特殊矩阵的压缩存储

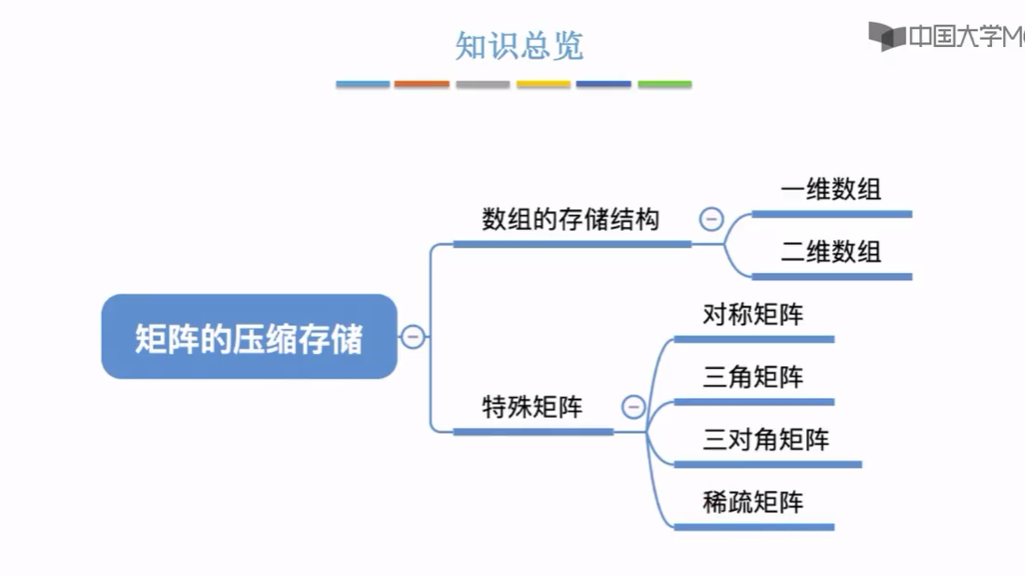
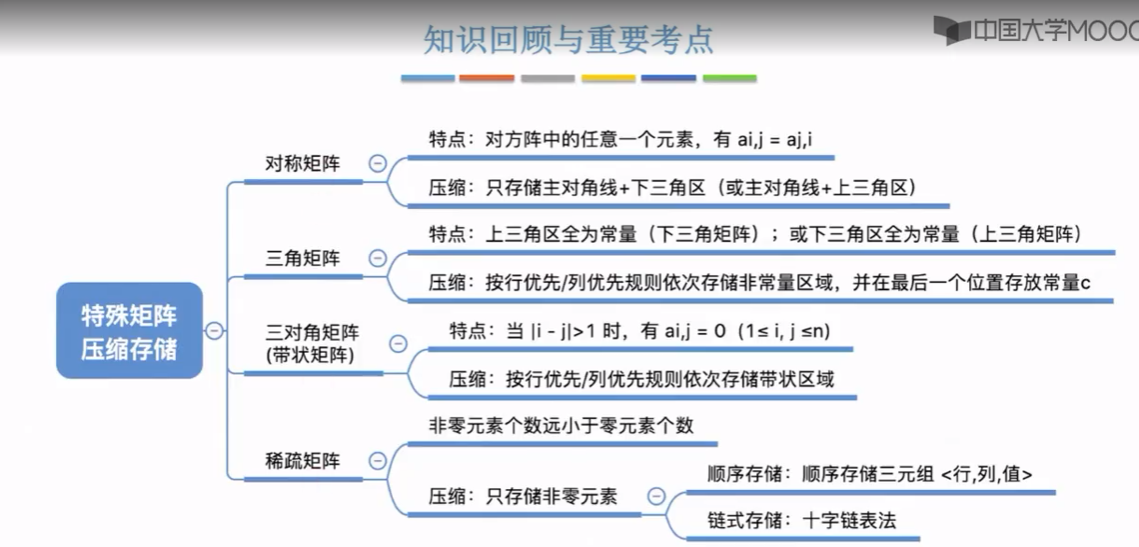
那由于矩阵可以很方便的使用数组来存储，所以我们首先会介绍一下一维数组和二维数组背后的一些实现细节。然后我们会介绍几种特殊矩阵，分别是对称矩阵，三角矩阵，三对角矩阵和稀疏矩阵。这几种矩阵可以用一些简单的策略来节省大量的存储空间。

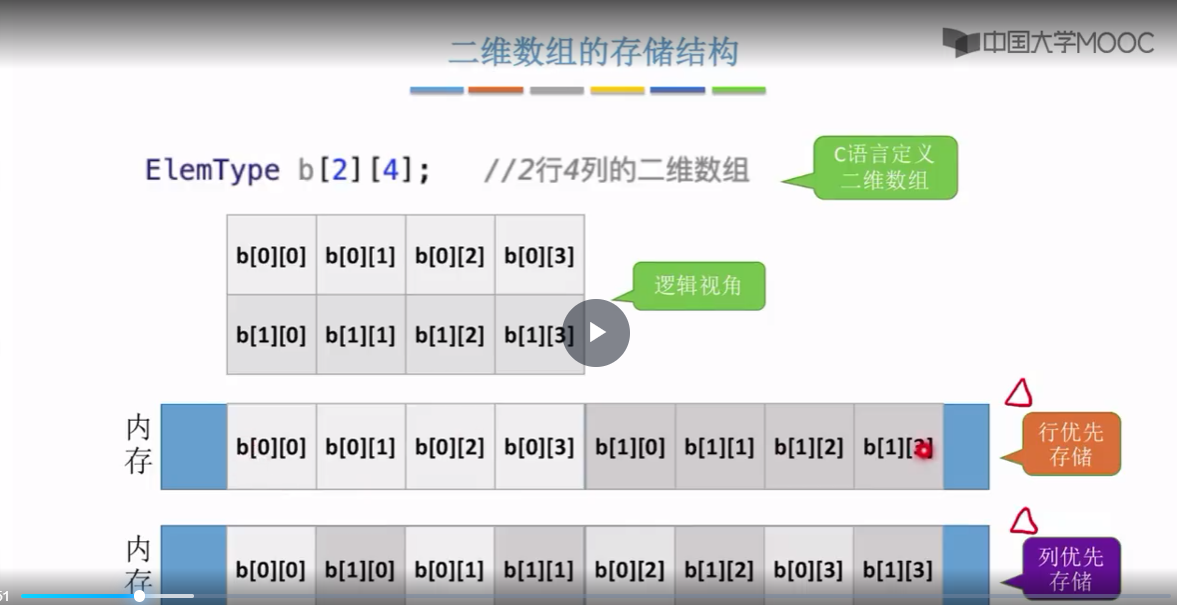
有这样的两种存储方法，第一种存储方法叫做行优先，也就是一行一行的存。就是先存第一行，

第一行存完了之后，紧接其后，再接着存第二行，这是行优先第二种存放方法是列优先。也就是先存第一列，这是第一列的两个元素，再存第二列，那这是第二列的两个元素，那之后的以此类推就是一列一列的存和一行一行的存。这就是两种不同的存储策略，分别是行优先和列优先，所以我们规定行优先或者规定列优先的存储原则。其实本质的目的是想要把这样的一个非线性的二维数组把它拉成一个线性的形状。因为刚才我们说过，计算机内存的这些存储空间都是线性的好，

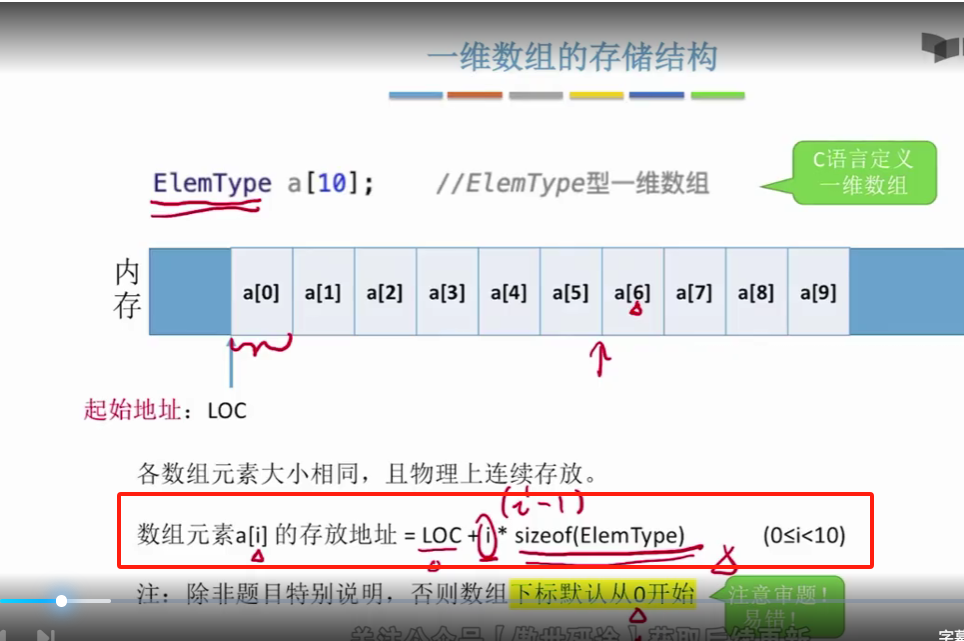
那把这些数据像这样有规律的存放到内存里边之后，所带来的好处就是可以实现随机存取。（这个是需要记住的）

那把这些数据像这样有规律的存放到内存里边之后，所带来的好处就是可以实现随机存取。也就是说，如果我们想要访问二维数组当中的某一个数据元素的话，那我们只需要给出这个元素所对应的行号和列号，那计算机就可以直接算出。这个行号和列号所对应的元素，它的存放地址到底是多少？

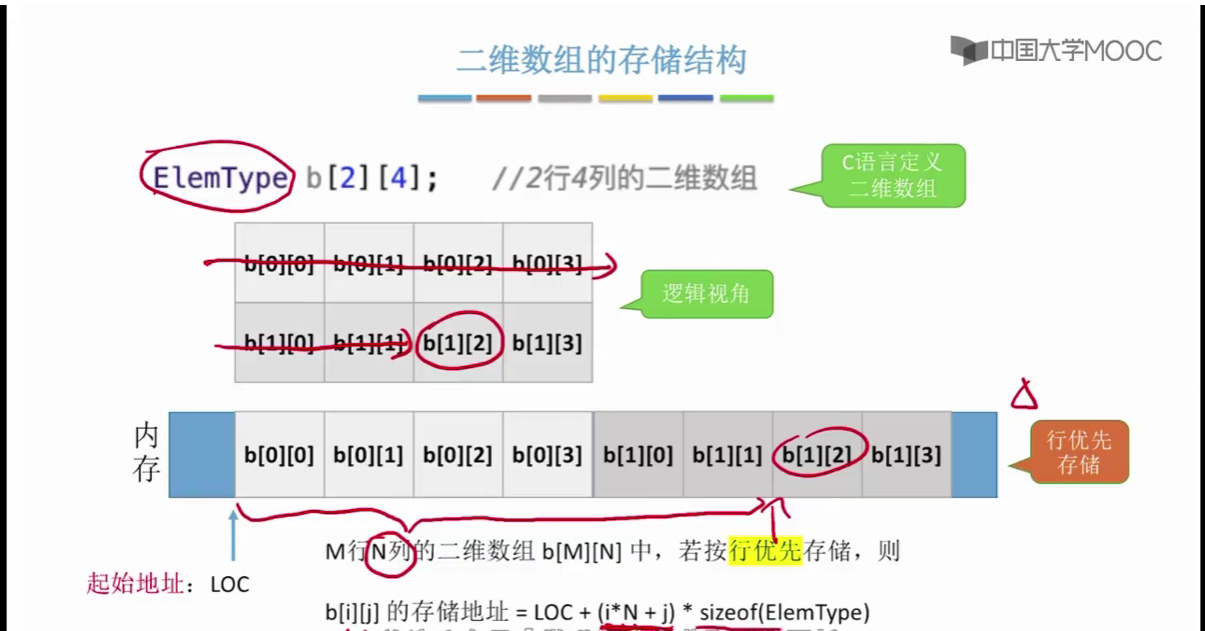
首先来看，如果采用行优先存储的话，那我们怎么计算某一个元素？它的存储地址呢？其实很简单，我们只需要算出它前面的这些数据元素总共占多少个字节，

然后再加上起始地址，那这不就是这个元素，它的存放地址吗？

所以只要我们给出一个二维数组的行号和列号。

那其实计算机就可以立即算出这个元素，所对应的存储地址，也就是说二维数组它也具有随机存取的特性

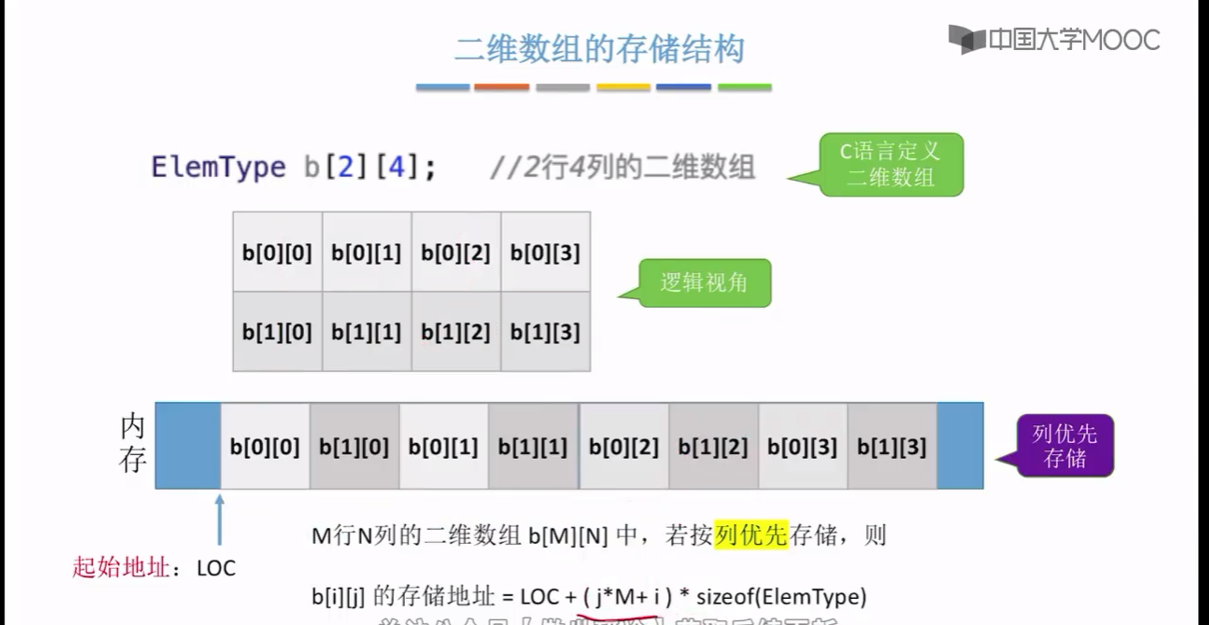
那这个地址的计算方法其实就是一个很简单的数学问题，我们在这个地方。主要是要理解什么叫列优先存储，什么叫行优先存储好，接下来我们才会正式进入这个小节的重点内容。怎么在计算机当中存储矩阵这种类型的数据？

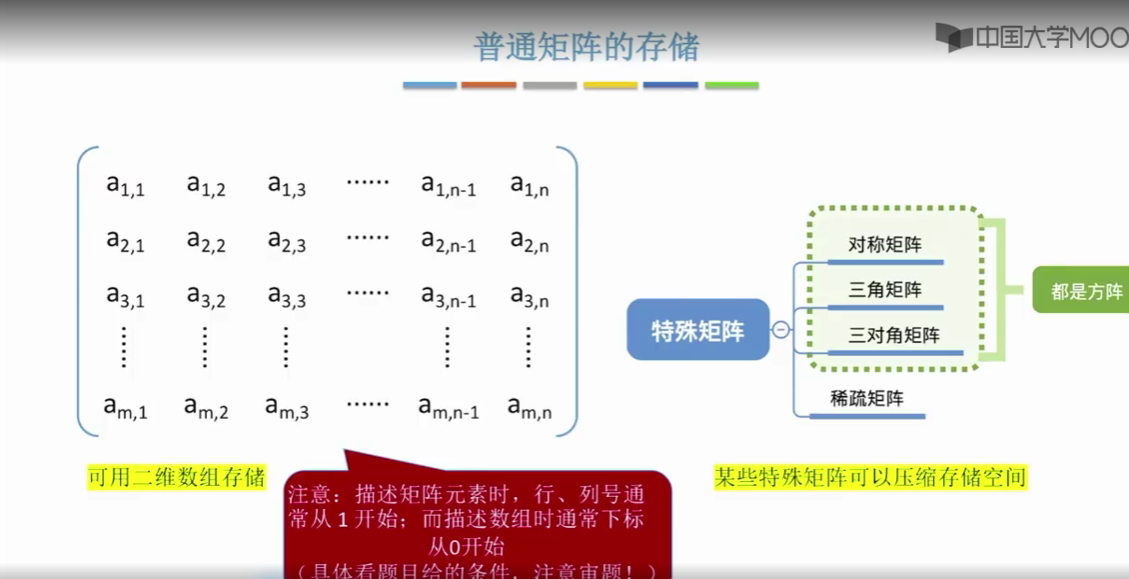
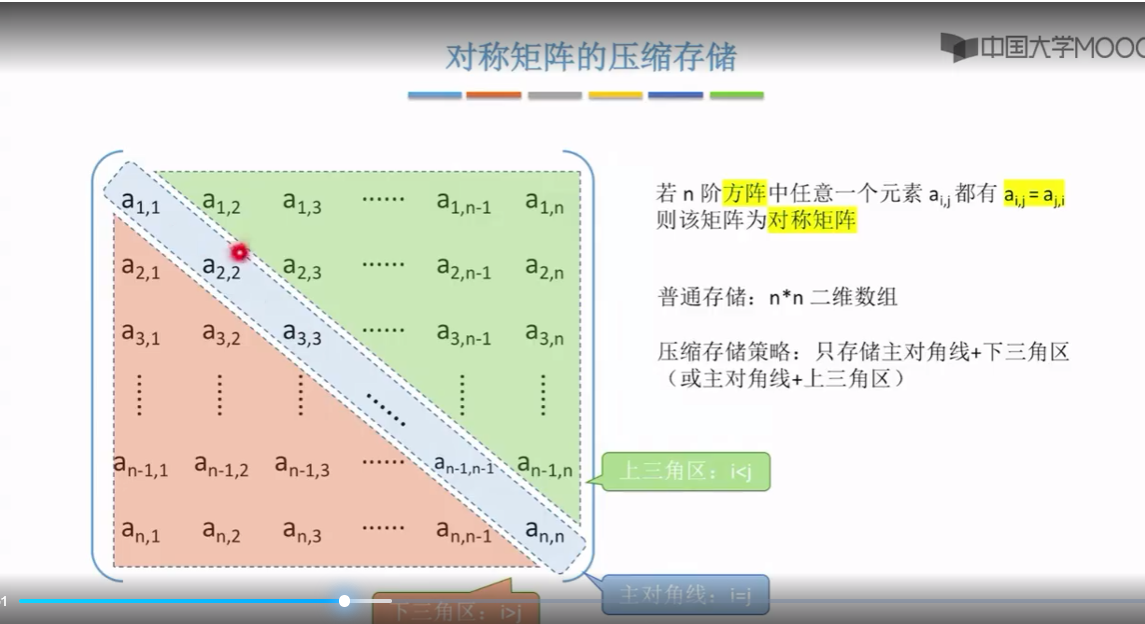
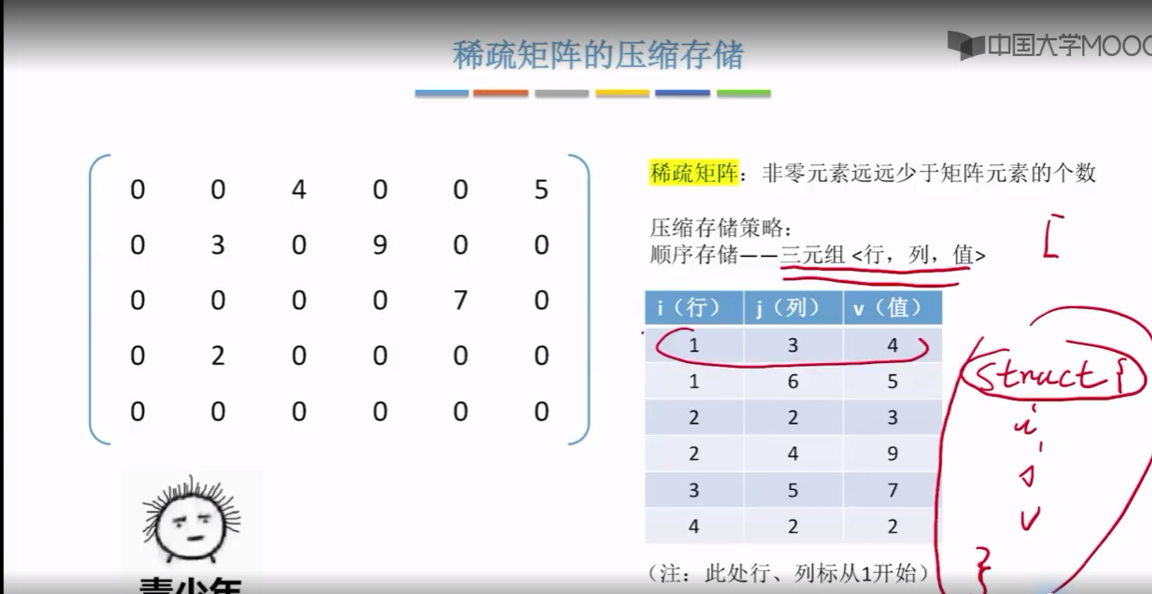
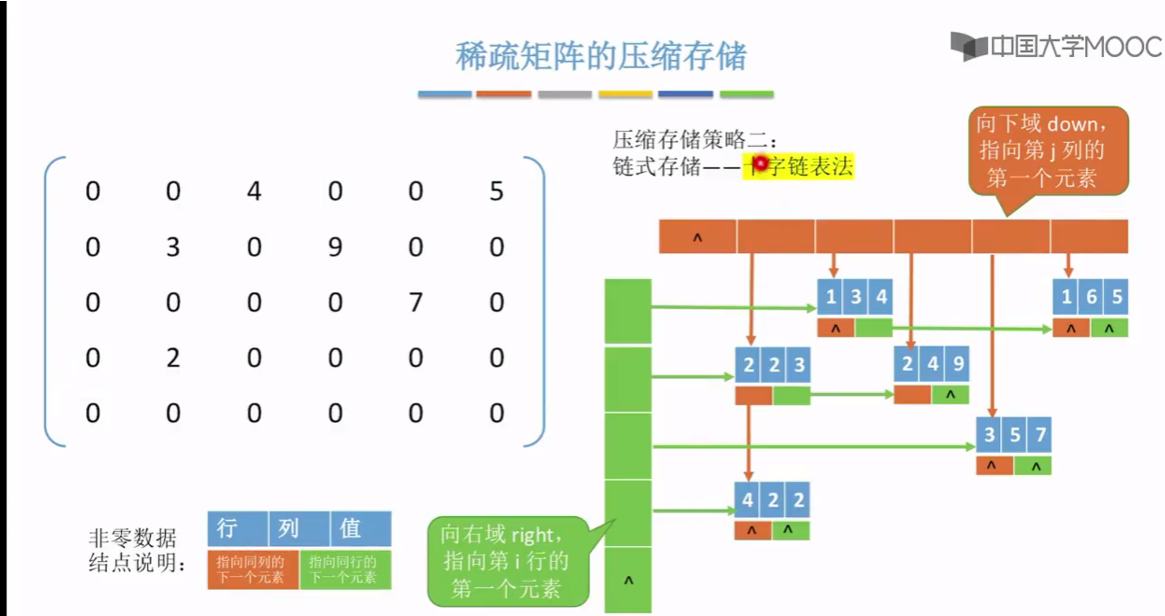
接下来分别看一下 压缩的存储策略

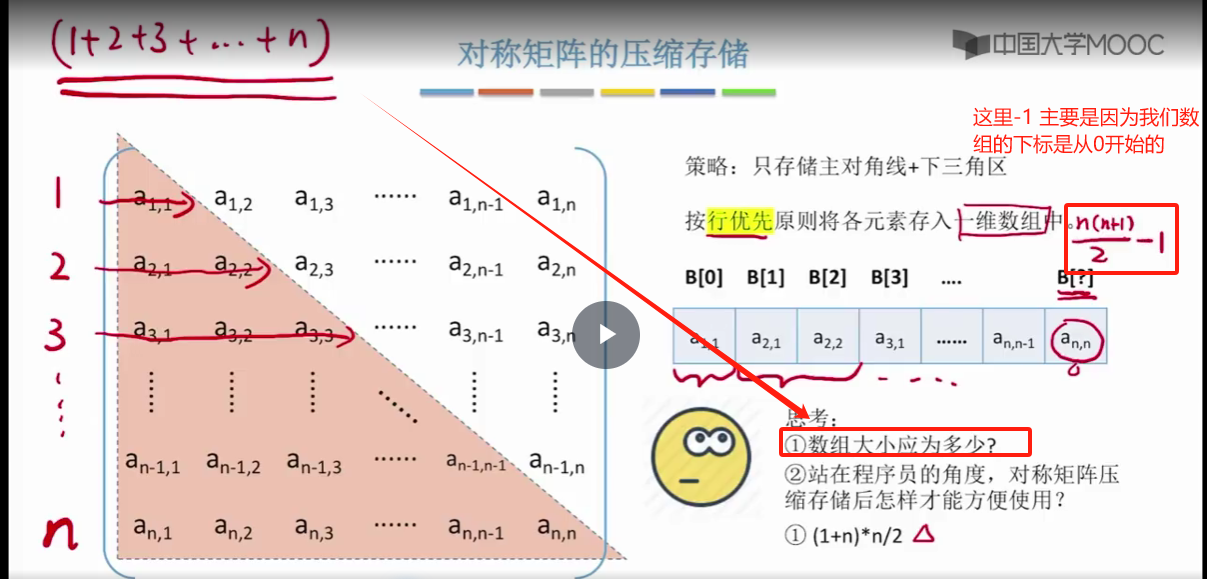
接下来要探讨的是第二个问题，就站在程序员的角度来看，我们把一个矩阵的数据存储之后。最终的目的其实是想要用这些数据，

对吧？好，那当你在用这些数据的时候，你肯定是希望从你的视角看到的是一个矩阵，而不是这样的一个一维数组。也就说你肯定是希望能够从这个矩阵的视角，用矩阵的元素下标来访问这些各个元素，而不是直接使用这个一维数组的某个下标。那为了实现这个目的，其实很简单的一个方法就是你可以自己实现一个映射函数

那这样的话，当你想要访问矩阵中的某一行某一列这个元素的时候。是不是只需要用这个映射函数一转，你就可以知道诶，它存放在这个数组里边的哪个位置好，所以这是把对称矩阵压缩存储之后，我们需要实现的很重要的一个东西。也是考研当中最喜欢考察的一个点。

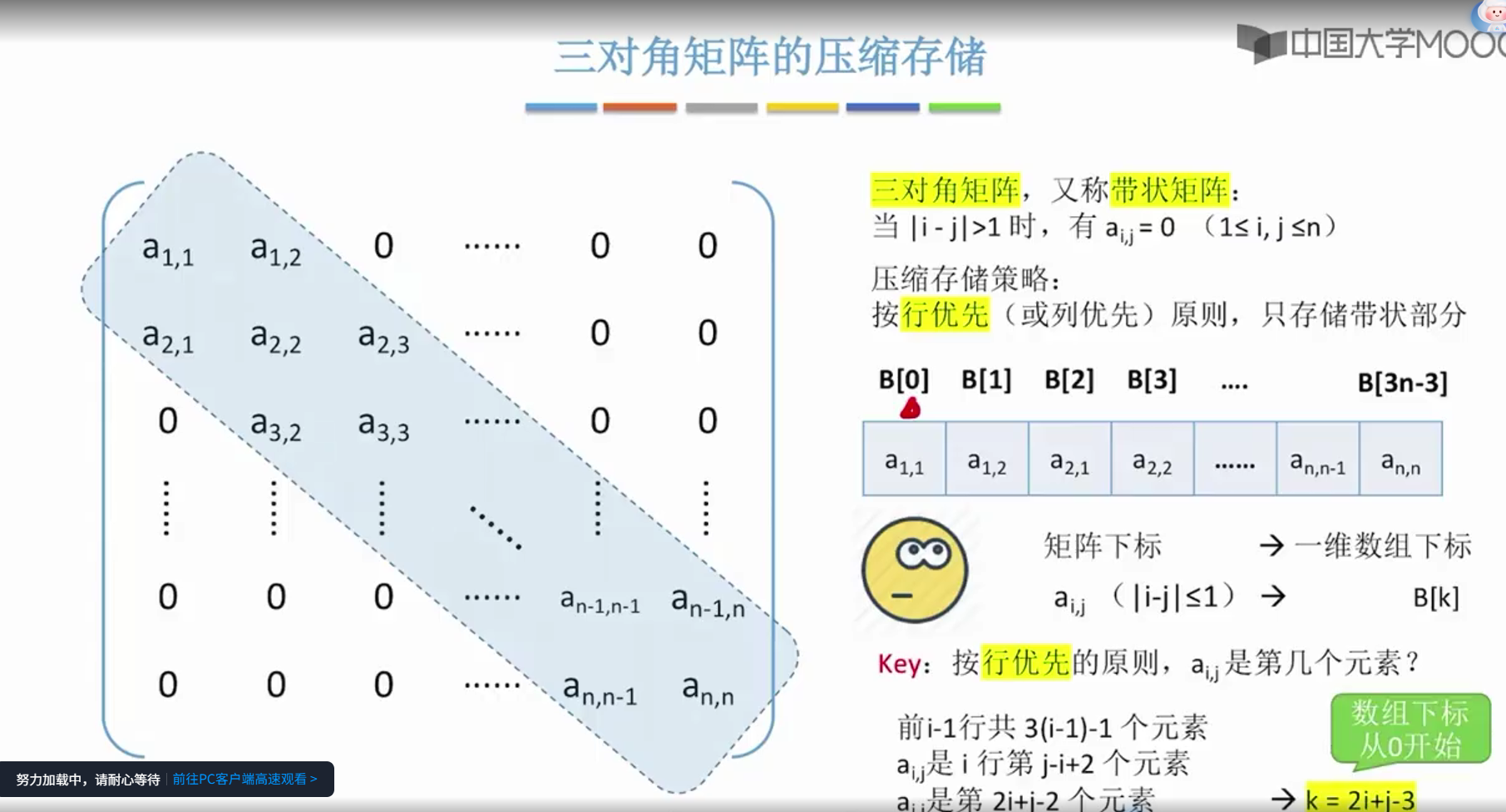
接下来就来探讨这个问题，就是怎么把矩阵的行号和列号把它映射为与之对应的数组下标

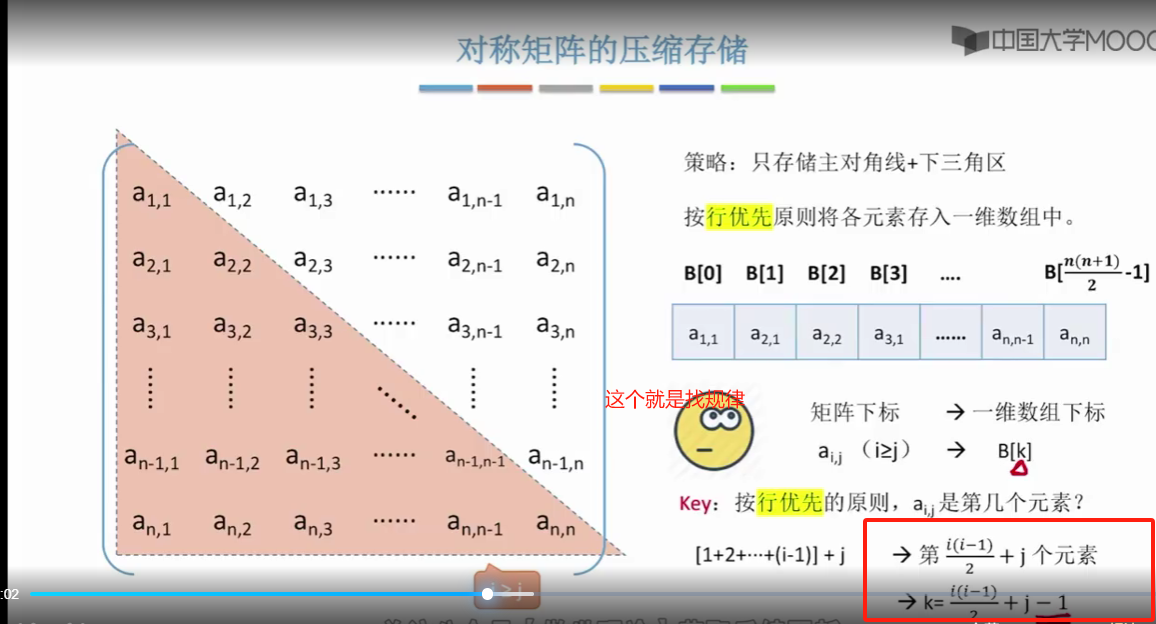
按列优先

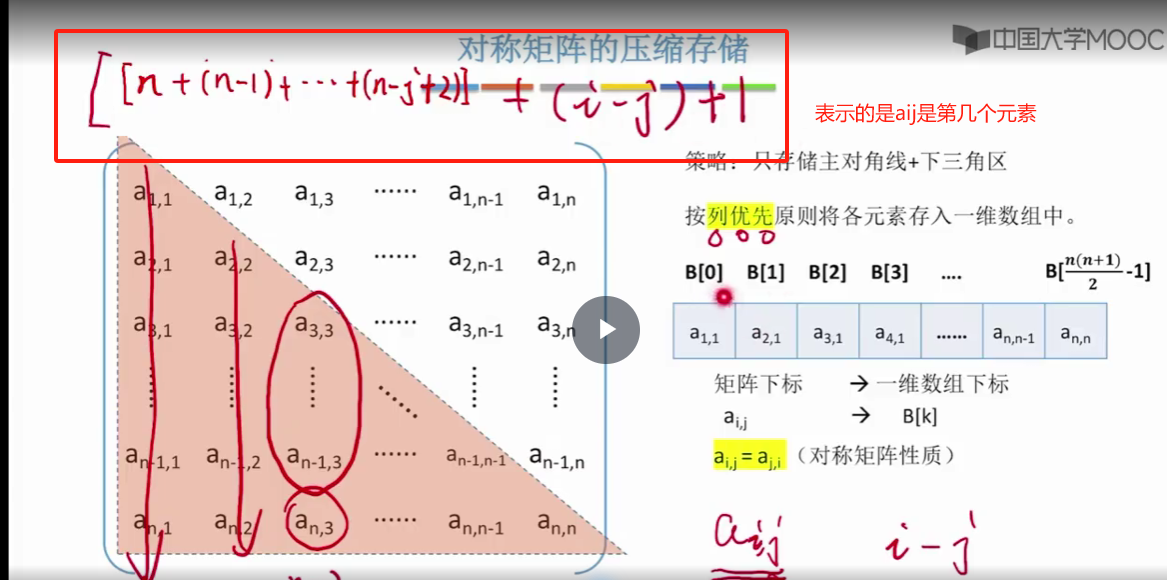
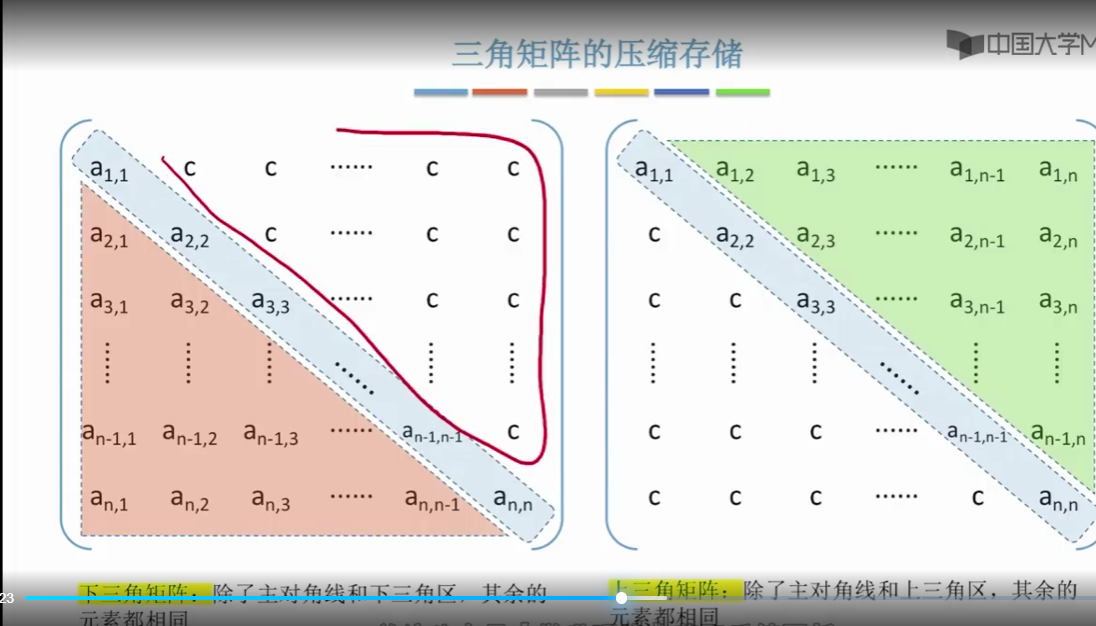
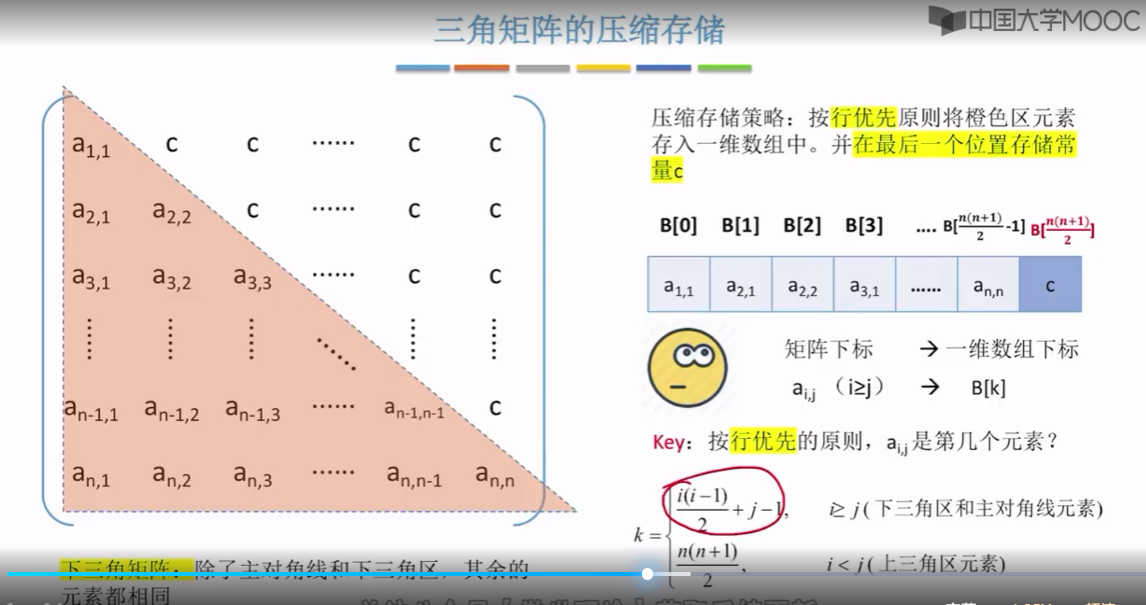
我们就需要把呃横号和列号把它映射为与之对应的数组下标。那计算方法是不是和对称矩阵一毛一样啊？你看这个式子都是一样的，唯一不同的是，如果我们此次要访问的是上三角区，也就是。行号小于列号I小于j的这个区域的话。那这个区域所有的元素，它们都是一个常量c，因此访问这个区域的任何一个元素。我们都应该把它映射到这个一维数组的最后一个位置（最后一个位置存放的数据就是常量c）