从头学 | 目标函数、梯度下降相关知识笔记（一）

很多基本的概念最近忘的有点多，简单回顾一些

---

---

1 目标函数、梯度下降

1.1 回归模型中的目标函数

在回归模型中，目标函数（即损失函数）通常设定为均方误差（MSE），其数学形式为：

导数形态为：
$$\frac{\partial L}{\partial {\hat{y}}_i}=\frac{2}{N}(y_i-{\hat{y}}_i)$$

MSE通过计算预测值与真实值的平均平方距离，将模型的“好坏”转化为可量化的数值。误差越小，模型拟合数据的能力越强。

回归模型的目标函数符合凸函数特性：

• 凸函数特性：在线性回归中，损失函数是凸函数，梯度下降能收敛到全局最优解；
• 非凸问题：在复杂模型（如神经网络）中，可能陷入局部最优，需通过调整学习率或初始化策略改进。

一些其他常见的目标函数：

目标函数	导数特性	算法影响
MSE	线性梯度，随误差增大而增强	易受异常值干扰，收敛震荡
交叉熵	梯度与误差直接相关	适合概率优化，收敛稳定
Huber损失	分段线性/恒定梯度	鲁棒性强，抗噪声能力优异
L1正则化	非连续梯度（符号函数）	导致参数稀疏化，特征选择

1.1.1 回归任务目标函数

(1) 均方误差（MSE）

定义：
$$L=\frac{1}{N}\sum _{i=1}^N(y_i-{\hat{y}}_i{)}^2$$
导数：
$$\frac{\partial L}{\partial {\hat{y}}_i}=\frac{2}{N}(y_i-{\hat{y}}_i)$$
特点：导数值与预测误差呈线性关系，对异常值敏感

(2) Huber损失

定义：分段函数（$\delta$为阈值参数）
$$L=\{\begin{array}{ll}\frac{1}{2}(y-\hat{y}{)}^2& |y-\hat{y}|\le \delta \\ \delta |y-\hat{y}|-\frac{1}{2}{\delta }^2& |y-\hat{y}|>\delta \end{array}$$
导数：
$$\frac{\partial L}{\partial \hat{y}}=\{\begin{array}{ll}-(y-\hat{y})& |y-\hat{y}|\le \delta \\ -\delta \cdot \text{sign}(y-\hat{y})& |y-\hat{y}|>\delta \end{array}$$
特点：结合MSE和MAE优点，对离群值鲁棒

1.1.2 分类任务目标函数

(1) 交叉熵损失（Cross-Entropy）

定义（二分类）：
$$L=-\frac{1}{N}\sum _{i=1}^N[y_i\log {\hat{y}}_i+(1-y_i)\log (1-{\hat{y}}_i)]$$
导数（Sigmoid激活时）：
$$\frac{\partial L}{\partial z_i}={\hat{y}}_i-y_i$$
特点：梯度与预测概率偏差直接相关，适合概率输出场景

(2) 对数损失（Log Loss）

定义（多分类）：
$$L=-\frac{1}{N}\sum _{i=1}^N\sum _{c=1}^C{y}_{i,c}\log {\hat{y}}_{i,c}$$
导数（Softmax激活时）：
$$\frac{\partial L}{\partial z_j}={\hat{y}}_j-y_j$$
特点：梯度体现预测概率与真实标签的差异

1.1.3 正则化项导数

• L1正则化：菱形的角点更容易与等高线相切。例如，若原始最优解在菱形外，正则化后的解会落在菱形的顶点（如坐标轴上），导致某些参数为0。
• L2正则化：圆形的边界与等高线相切时，切点通常不在坐标轴上，因此参数整体被压缩但不会稀疏。

特性	L1正则化	L2正则化
目标函数惩罚项	绝对值之和（(\sum |\theta_j|)）	平方和（(\sum \theta_j^2)）
参数更新方向	趋向于零	趋向于缩小但非零
特征选择能力	强（稀疏性）	弱（平滑性）
适用场景	高维特征选择、模型压缩	防止过拟合、处理共线性

(1) L2正则化

定义：
$$R=\frac{\lambda }{2}\Vert \theta {\Vert }^2$$
导数：
$$\frac{\partial R}{\partial {\theta }_j}=\lambda {\theta }_j$$
特点：导数为线性，导致参数收缩效应
L2正则化的解空间是圆形，参数被限制在一个圆形区域内，最优解通常出现在边界上的非角点位置，参数值较小但非零，整体分布平滑。

(2) L1正则化

定义：
$$R=\lambda \Vert \theta {\Vert }_1$$

因为此时Loss求解空间（就是导数）是菱形，参数被限制在一个菱形区域内，最优解倾向于出现在菱形的顶点（即坐标轴上），导致某些参数为0，产生稀疏性。

导数：
$$\frac{\partial R}{\partial {\theta }_j}=\lambda \cdot \text{sign}({\theta }_j)$$
特点：导数为常数，产生稀疏解

---

1.2 梯度下降的更新原理

通过沿目标函数梯度（下降最快方向）的负方向逐步调整参数，使损失函数最小化。
也就是沿着函数公式的导数方向，进行迭代运算。

如果在回归模型当中就是回归系数W与截距项B在不断变化，
来寻找均方误差达到最小值时候，W、B分别是什么。

其参数更新公式为：

梯度下降的步骤是：

• 1.随机选择一个起点（初始参数值）；
• 2.观察四周最陡的下坡方向（计算梯度）；
• 3.迈出一步（调整参数）；
• 4.重复直到到达山谷底部（损失函数最小）。

1.2.1 批量梯度下降（BGD）与随机梯度下降（SGD）

BGD：每次参数更新需要遍历所有样本，计算整体数据的平均梯度。
白话：就像考试前把整本教材复习一遍再调整学习方法，虽然全面但耗时长。
SGD：每次随机选择一批batch_size样本计算梯度，立刻更新参数。
白话：像边做题边改错，每做一道题就调整一次思路，速度快但容易受个别难题影响。

Mini-Batch SGD的常见实践：实际应用中，更常用的是小批量梯度下降（Mini-Batch SGD），即每次从打乱后的数据中按固定步长抽取一批样本（如32、64个）。例如网页4的代码若修改为

for i in range(0, m, batch_size):batch = X_b[i:i+batch_size]  # 抽取小批量

1.3 导数的意义

导数（尤其是梯度）是梯度下降类优化算法的基础。
通过计算目标函数关于模型参数的偏导数，可以确定 参数更新方向与步长。!!!

例如：

• 梯度下降：参数更新公式为 ${\theta }_{k+1}={\theta }_k-\alpha {\nabla }_{\theta }L({\theta }_k)$，其中梯度 ${\nabla }_{\theta }L$ 由导数计算得到
• 自适应优化器：如Adam、RMSProp等算法依赖梯度的一阶矩和二阶矩统计量

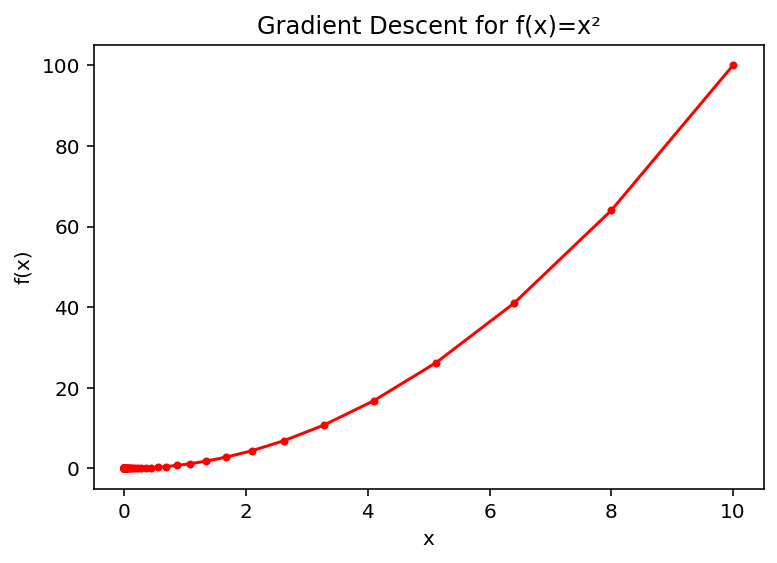
下面贴一个python关于f(x) = x^2 的案例：

import numpy as np
import matplotlib.pyplot as plt
import copydef f(x):return x**2def df(x):return 2*xdef gradient_descent(x0, lr=0.1, tol=1e-6, max_iter=1000):x = x0history = [x]for _ in range(max_iter):_x = copy.deepcopy(x)grad = df(x)if abs(grad) < tol:breakx -= lr * grad # lr-学习率history.append(x)print(f' 原来的x-{round(_x,4)}; x求导值-{round(grad,4)}; 更新x-{round(x,4)}  ')return x, np.array(history)# 参数设置
x0 = 10.0
x_min, history = gradient_descent(x0)# 可视化
plt.plot(history, f(history), 'ro-', markersize=3)
plt.xlabel('x')
plt.ylabel('f(x)')
plt.title('Gradient Descent for f(x)=x²')
plt.show()
print(f"最优解 x = {x_min:.6f}")

可以看到：

grad = df(x)
x -= lr * grad # lr-学习率

通过df(x)计算得到了gradient梯度之后，会更新x，其中LR是学习率

其他：

神经网络中反向传播的数学基础
在神经网络中，导数通过链式法则实现误差的逐层反向传播：

• 计算损失函数对输出层权重的偏导数 $\frac{\partial L}{\partial W^{(L)}}$
• 通过递归计算隐层权重梯度 $\frac{\partial L}{\partial W^{(l)}}=\frac{\partial L}{\partial z^{(l)}}\cdot \frac{\partial z^{(l)}}{\partial W^{(l)}}$，其中 $z^{(l)}$ 为第$l$层输出

模型特征选择与可解释性

• 通过计算特征对损失的偏导数 $\frac{\partial L}{\partial x_i}$，可量化特征重要性（如Integrated Gradients方法）
• 导数形态分析可揭示模型决策边界特性（如ReLU激活函数的梯度稀疏性）

---

2 python代码案例

2.1 简单的单变量二次函数优化

import numpy as np
import matplotlib.pyplot as plt
import copy# 原来函数
def f(x):return x**2# 求导函数
def df(x):return 2*x# 梯度下降函数
def gradient_descent(x0, lr=0.1, tol=1e-6, max_iter=1000):x = x0history = [x]for _ in range(max_iter):_x = copy.deepcopy(x)grad = df(x)if abs(grad) < tol:breakx -= lr * grad # lr-学习率history.append(x)print(f' 原来的x-{round(_x,4)}; x求导值-{round(grad,4)}; 更新x-{round(x,4)}  ')return x, np.array(history)# 参数设置
x0 = 10.0
x_min, history = gradient_descent(x0)# 可视化
plt.plot(history, f(history), 'ro-', markersize=3)
plt.xlabel('x')
plt.ylabel('f(x)')
plt.title('Gradient Descent for f(x)=x²')
plt.show()
print(f"最优解 x = {x_min:.6f}")

其中

 x -= lr * grad # lr-学习率

很关键，就是在更新X，lr为学习率，grad为导数，因为一阶导是线性的，所以方向比较一致以及明显

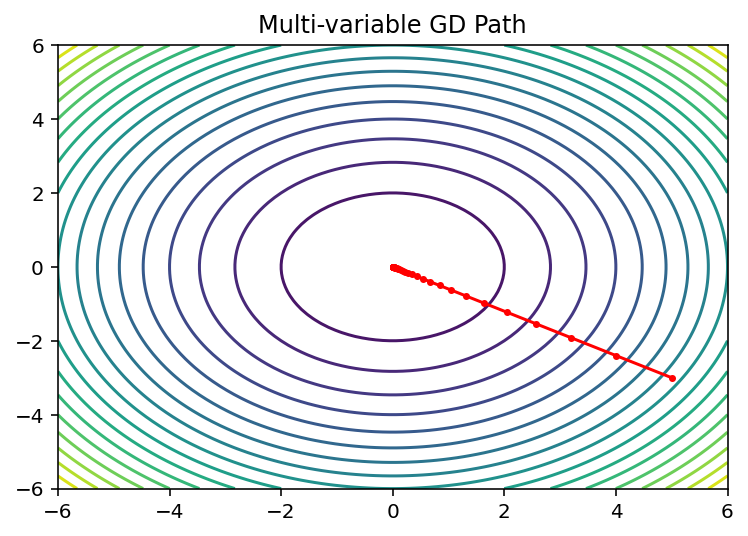
2.2 多变量二次函数优化

def f(x, y):return x**2 + y**2def grad(x, y):return 2*x, 2*ydef multivariable_gd(x0, y0, lr=0.1, tol=1e-6, max_iter=1000):x, y = x0, y0history = [(x, y)]for _ in range(max_iter):gx, gy = grad(x, y)if np.sqrt(gx**2 + gy**2) < tol:breakx -= lr * gxy -= lr * gyhistory.append((x, y))return (x, y), np.array(history)# 参数设置
x0, y0 = 5.0, -3.0
(x_min, y_min), history = multivariable_gd(x0, y0)# 可视化
X, Y = np.meshgrid(np.linspace(-6,6,100), np.linspace(-6,6,100))
Z = f(X, Y)
plt.contour(X, Y, Z, levels=20)
plt.plot(history[:,0], history[:,1], 'r.-', markersize=5)
plt.title('Multi-variable GD Path')
plt.show()
print(f"最优解 (x, y) = ({x_min:.6f}, {y_min:.6f})")

跟单变量二次函数类似，此时是两个参数求偏导，然后分别进行更新

        x -= lr * gxy -= lr * gy

2.3 多目标函数优化

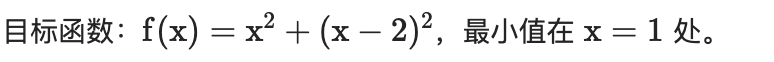
def f(x):return x**2 + (x-2)**2def df(x):return 2*x + 2*(x-2)  # 两个目标函数的梯度之和def multi_objective_gd(x0, lr=0.1, tol=1e-6, max_iter=1000):x = x0history = [x]for _ in range(max_iter):grad = df(x)if abs(grad) < tol:breakx -= lr * gradhistory.append(x)return x, np.array(history)# 运行与可视化
x0 = 5.0
x_min, history = multi_objective_gd(x0)
plt.plot(history, label='x trajectory')
plt.axhline(1, color='gray', linestyle='--', label='True minimum')
plt.xlabel('Iteration')
plt.ylabel('x')
plt.legend()
plt.show()
print(f"最优解 x = {x_min:.6f}")

相对来说，就是跟单变量二次函数类似，就是求导的时候，公式会兼顾多个目标，曲线迭代的过程跟单变量二次类似

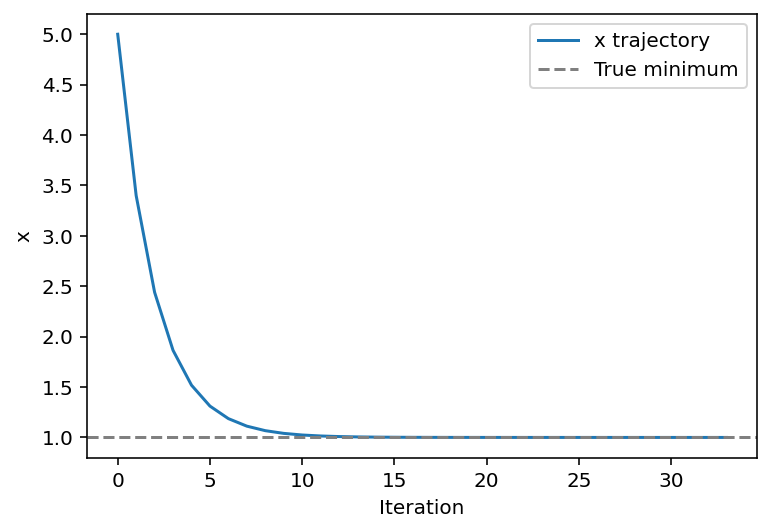
2.4 线性回归（均方误差优化）

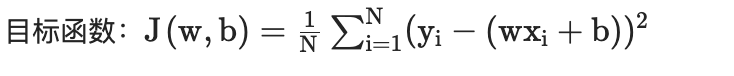
导数：
$$\frac{\partial L}{\partial {\hat{y}}_i}=\frac{2}{N}(y_i-{\hat{y}}_i)$$
特点：导数值与预测误差呈线性关系，对异常值敏感

# 生成模拟数据
np.random.seed(42)
X = np.linspace(0, 10, 100)
y = 2*X + 3 + np.random.randn(100)*2def mse_loss(w, b, X, y):return np.mean((y - (w*X + b))**2)def gradient(w, b, X, y):dw = -2 * np.mean(X*(y - (w*X + b)))db = -2 * np.mean(y - (w*X + b))return dw, dbdef linear_regression_gd(w0=0, b0=0, lr=0.01, max_iter=1000):w, b = w0, b0loss_history = []for _ in range(max_iter):dw, db = gradient(w, b, X, y)w -= lr * dwb -= lr * dbloss_history.append(mse_loss(w, b, X, y))return (w, b), loss_history# 训练与可视化
(w_opt, b_opt), losses = linear_regression_gd()
plt.plot(losses)
plt.xlabel('Iterations')
plt.ylabel('MSE Loss')
plt.title('Linear Regression Training')
plt.show()
print(f"最优参数：w={w_opt:.2f}, b={b_opt:.2f}")

更新回归系数以及截距项，梯度求解过程跟之前类似：

def gradient(w, b, X, y):dw = -2 * np.mean(X*(y - (w*X + b)))db = -2 * np.mean(y - (w*X + b))return dw, db
dw, db = gradient(w, b, X, y)
w -= lr * dw
b -= lr * db

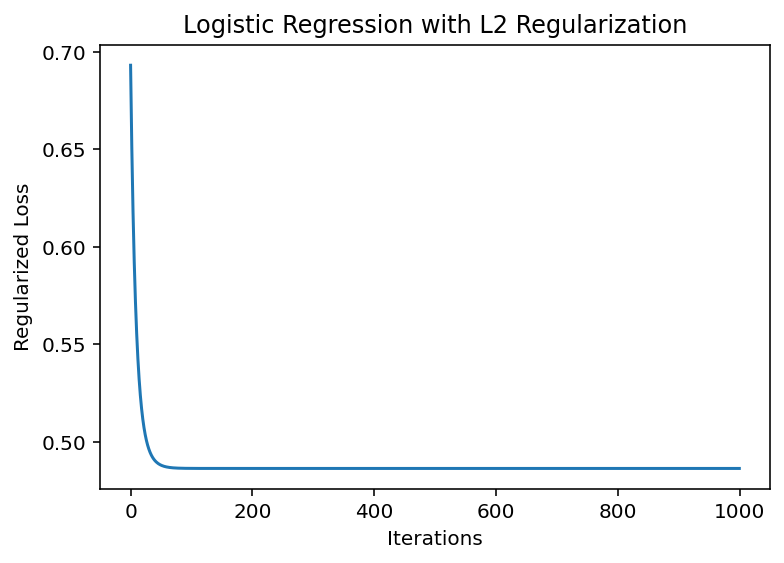
2.5 带L2正则化的逻辑回归

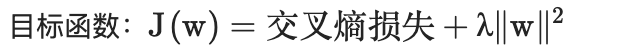
导数：
$$\frac{\partial R}{\partial {\theta }_j}=\lambda {\theta }_j$$
特点：导数为线性，导致参数收缩效应

from sklearn.datasets import make_classification# 生成二分类数据
X, y = make_classification(n_samples=100, n_features=2, n_informative=2, n_redundant=0)
y = y*2 -1  # 标签转为±1def sigmoid(z):return 1 / (1 + np.exp(-z))def l2_regularized_loss(w, X, y, lambda_=0.1):z = np.dot(X, w)loss = np.mean(np.log(1 + np.exp(-y*z))) + lambda_ * np.sum(w**2)grad = -np.mean((y * X.T * sigmoid(-y*z)).T, axis=0) + 2*lambda_*wreturn loss, graddef logistic_gd(X, y, lr=0.1, lambda_=0.1, max_iter=1000):w = np.zeros(X.shape[1](@ref)loss_history = []for _ in range(max_iter):loss, grad = l2_regularized_loss(w, X, y, lambda_)w -= lr * gradloss_history.append(loss)return w, loss_history# 添加偏置项
X = np.hstack([X, np.ones((X.shape[0],1))])
w_opt, losses = logistic_gd(X, y)# 可视化训练过程
plt.plot(losses)
plt.xlabel('Iterations')
plt.ylabel('Regularized Loss')
plt.title('Logistic Regression with L2 Regularization')
plt.show()
print(f"最终权重：{w_opt}")

逻辑回归是sigmod