当前位置：首页 > ai >正文

新手蓝桥杯冲击国一练习题单(四)

ai 2025/7/27 21:42:23

2025蓝桥杯省赛已结束，接下来是冲击国赛的时间

此题单为算法基础精选题单，包含蓝桥杯常考考点以及各种经典算法，可以帮助你打牢基础，查漏补缺。

本题单目标是冲击蓝桥杯省一国一，团体程序天梯赛个人国三、XCPC区域赛铜/银奖

本次题单的重点是图论、模拟(练习暴力写题能力)、填空题

图论是蓝桥杯常考并且较难的内容，如果想要拿到高分，学会常用的几个图论算法是很有必要的

填空题是蓝桥杯中容易拉分的题型，在填空题中常常会有许多坑

本次题单的题目及类型如下：

图论

Dijkstra求最短路 I 模板题—acwing

Dijkstra求最短路 II 模板题—acwing

有边数限制的最短路模板题—acwing

spfa求最短路模板题—acwing

Floyd求最短路模板题—acwing

狡兔 k 窟—2024蓝桥杯省赛真题

星际旅行—2024蓝桥杯cb组省赛真题

模拟

I Love 1543——codeforces周赛

分布式队列—2024蓝桥杯省赛真题

填空题练习

报数游戏—2024蓝桥杯省赛真题

类斐波那契循环数——2024蓝桥杯真题

更多题单请看：

蓝桥杯冲击国一练习题单(一)

蓝桥杯进制问题秒破解法|冲击国一题单(二)

蓝桥杯新手算法练习题单Java|冲击国一(三)

一、图论

1.1Dijkstra求最短路 I

我是补题链接点我跳转写题

给定一个 n个点 m条边的有向图，图中可能存在重边和自环，所有边权均为正值。

请你求出 1 号点到 n 号点的最短距离，如果无法从 1 号点走到 n 号点，则输出 −1。

输入格式

第一行包含整数 n 和 m。

接下来 mm 行每行包含三个整数 x,y,z，表示存在一条从点 x 到点 y 的有向边，边长为 z。

输出格式

输出一个整数，表示 1 号点到 n 号点的最短距离。

如果路径不存在，则输出 −1。

数据范围

1≤n≤500,
1≤m≤105,
图中涉及边长均不超过10000。

输入样例：

输出样例：

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.StreamTokenizer;
import java.util.*;public class Main {static int n,m,INF=1000000000,N=510;static int dis[]=new int[N];static boolean flag[]=new boolean[N];static int map[][]=new int[N][N];public static void main(String[] args) throws IOException {Read sc=new Read();n=sc.nextInt();m=sc.nextInt();Arrays.fill(dis,INF);for(int i=1;i<N;i++){for(int j=1;j<N;j++){map[i][j]=INF;}}for(int i=0;i<m;i++){int a=sc.nextInt();int b=sc.nextInt();int c=sc.nextInt();map[a][b]= Math.min(map[a][b],c);}int ans=dijk(1);if(ans==INF) System.out.println(-1);else System.out.println(ans);}static int dijk(int start){dis[start]=0;for(int i=0;i<n;i++){int t=-1;for(int j=1;j<=n;j++){if(!flag[j]&&(t==-1||dis[t]>dis[j])){t=j;}}flag[t]=true;for(int j=1;j<=n;j++){dis[j]=Math.min(dis[j],dis[t]+map[t][j]);}}return dis[n];}
}
class Read {BufferedReader bfr = new BufferedReader(new InputStreamReader(System.in));StreamTokenizer st = new StreamTokenizer(bfr);public int nextInt() throws IOException {st.nextToken();return (int) st.nval;}public long nextLong() throws IOException {st.nextToken();return (long) st.nval;}public Double nextDouble() throws IOException {st.nextToken();return (Double) st.nval;}public String nextLine() throws IOException {return bfr.readLine();}public String next() throws IOException {return st.sval;}
}

1.2Dijkstra求最短路 II

我是补题链接点我跳转写题

给定一个 n 个点 m 条边的有向图，图中可能存在重边和自环，所有边权均为非负值。

请你求出 1 号点到 n 号点的最短距离，如果无法从 1 号点走到 n 号点，则输出 −1。

输入格式

第一行包含整数 n 和 m。

接下来 m 行每行包含三个整数 x,y,z，表示存在一条从点 x 到点 y 的有向边，边长为 z。

输出格式

输出一个整数，表示 1 号点到 n 号点的最短距离。

如果路径不存在，则输出 −1。

数据范围

1≤n,m≤1.5×105
图中涉及边长均不小于 0，且不超过 10000
数据保证：如果最短路存在，则最短路的长度不超过 109。

输入样例：

输出样例：

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.StreamTokenizer;
import java.util.*;public class Main {static int N=200010,n,m,INF=100000000,idx;static int dis[]=new int[N],w[]=new int[N],val[]=new int[N],id[]=new int[N],next[]=new int[N];static boolean flag[]=new boolean[N];public static void main(String[] args) throws IOException {Read sc=new Read();n=sc.nextInt();m=sc.nextInt();Arrays.fill(dis,INF);Arrays.fill(id,-1);for(int i=1;i<=m;i++){int a=sc.nextInt();int b= sc.nextInt();int c=sc.nextInt();add(a,b,c);}int ans=dijk2(1);if(ans>=INF/2) System.out.println(-1);else System.out.println(ans);}static int dijk2(int start){dis[start]=0;Queue<dj2> queue=new PriorityQueue<>();queue.offer(new dj2(start,0));while(!queue.isEmpty()){dj2 t=queue.poll();if(flag[t.id])continue;flag[t.id]=true;for (int i=id[t.id];i!=-1;i=next[i]){int j=val[i];if(dis[j]>dis[t.id]+w[i]){dis[j]=dis[t.id]+w[i];queue.offer(new dj2(j,dis[j]));}}}return dis[n];}static void add(int a,int b,int c){val[idx]=b;next[idx]=id[a];w[idx]=c;id[a]=idx++;}
}
class dj2 implements Comparable<dj2>{int id;int d;public dj2(int id,int d){this.id=id;this.d=d;}@Overridepublic int compareTo(dj2 o) {return this.d-o.d;}
}
class Read {BufferedReader bfr = new BufferedReader(new InputStreamReader(System.in));StreamTokenizer st = new StreamTokenizer(bfr);public int nextInt() throws IOException {st.nextToken();return (int) st.nval;}public long nextLong() throws IOException {st.nextToken();return (long) st.nval;}public Double nextDouble() throws IOException {st.nextToken();return (Double) st.nval;}public String nextLine() throws IOException {return bfr.readLine();}public String next() throws IOException {return st.sval;}
}

1.3有边数限制的最短路

我是补题链接点我跳转写题

给定一个 n 个点 m 条边的有向图，图中可能存在重边和自环， 边权可能为负数。

请你求出从 1 号点到 n 号点的最多经过 k 条边的最短距离，如果无法从 1 号点走到 n 号点，输出 impossible。

注意：图中可能 存在负权回路 。

输入格式

第一行包含三个整数 n,m,k

接下来 m 行，每行包含三个整数 x,y,z表示存在一条从点 x 到点 y 的有向边，边长为 z。

点的编号为 1∼n

输出格式

输出一个整数，表示从 1 号点到 n 号点的最多经过 k 条边的最短距离。

如果不存在满足条件的路径，则输出 impossible。

数据范围

1≤n,k≤500
1≤m≤10000
1≤x,y≤n
任意边长的绝对值不超过 10000

输入样例：

输出样例：


import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
import java.util.Scanner;public class Main {static int n,m,k,INF=1000000000,N=1000;static List<edge> map=new ArrayList<>();static int dis[]=new int[N],backup[]=new int[N];public static void main(String[] args) {// TODO 自动生成的方法存根Scanner sc=new Scanner(System.in);Arrays.fill(dis, INF);n=sc.nextInt();m=sc.nextInt();k=sc.nextInt();for(int i=1;i<=m;i++){int a=sc.nextInt();int b=sc.nextInt();int c=sc.nextInt();map.add(new edge(a, b, c));}int ans=tbellman(1);if(ans>=INF/2)System.out.println("impossible");else System.out.println(ans);}static int tbellman(int start){dis[start]=0;for(int i=0;i<k;i++){backup=Arrays.copyOf(dis, dis.length);for(int j=0;j<m;j++){int a=map.get(j).a;int b=map.get(j).b;int w=map.get(j).c;dis[b]=Math.min(dis[b], backup[a]+w);}}return dis[n];}}
class edge{int a;int b;int c;public edge(int a,int b,int c){this.a=a;this.b=b;this.c=c;}
}

1.4 spfa求最短路

我是补题链接点我跳转写题

给定一个 n 个点 m 条边的有向图，图中可能存在重边和自环， 边权可能为负数。

请你求出 1 号点到 n 号点的最短距离，如果无法从 1 号点走到 n 号点，则输出 impossible。

数据保证不存在负权回路。

输入格式

第一行包含整数 n 和 m。

接下来 mm 行每行包含三个整数 x,y,z表示存在一条从点 x 到点 y 的有向边，边长为 z。

输出格式

输出一个整数，表示 1 号点到 n 号点的最短距离。

如果路径不存在，则输出 impossible。

数据范围

1≤n,m≤105
图中涉及边长绝对值均不超过 10000

输入样例：

输出样例：

import java.util.Arrays;
import java.util.LinkedList;
import java.util.Queue;
import java.util.Scanner;public class Main {static int N=200000,n,m,INF=1000000000,idx;static int w[]=new int[N],next[]=new int[N],val[]=new int[N],id[]=new int[N],dis[]=new int[N];static boolean flag[]=new boolean[N];public static void main(String[] args) {// TODO 自动生成的方法存根Scanner sc=new Scanner(System.in);n=sc.nextInt();m=sc.nextInt();Arrays.fill(dis, INF);Arrays.fill(id, -1);for(int i=1;i<=m;i++){int a=sc.nextInt();int b=sc.nextInt();int c=sc.nextInt();add(a,b,c);}int ans=tspfa(1);if(ans>=INF/2) System.out.println("impossible");else System.out.println(dis[n]);}static int tspfa(int start){dis[start]=0;Queue<Integer> queue=new LinkedList<>();queue.offer(start);flag[start]=true;while(!queue.isEmpty()){int t=queue.poll();flag[t]=false;for(int i=id[t];i!=-1;i=next[i]){int j=val[i];if(dis[j]>dis[t]+w[i]){dis[j]=dis[t]+w[i];if(!flag[j]){queue.offer(j);flag[j]=true;}}}}return dis[n];}static void add(int a,int b,int c){val[idx]=b;next[idx]=id[a];w[idx]=c;id[a]=idx++;}}

1.5Floyd求最短路

我是补题链接点我跳转写题

给定一个 n 个点 m 条边的有向图，图中可能存在重边和自环，边权可能为负数。

再给定 k 个询问，每个询问包含两个整数 x 和 y，表示查询从点 x 到点 y 的最短距离，如果路径不存在，则输出 impossible。

数据保证图中不存在负权回路。

输入格式

第一行包含三个整数 n,m,k

接下来 m 行，每行包含三个整数 x,y,z，表示存在一条从点 x 到点 y 的有向边，边长为 z。

接下来 k 行，每行包含两个整数 x,y，表示询问点 x 到点 y 的最短距离。

输出格式

共 k 行，每行输出一个整数，表示询问的结果，若询问两点间不存在路径，则输出 impossible。

数据范围

1≤n≤200
1≤k≤n2
1≤m≤20000
图中涉及边长绝对值均不超过 10000

输入样例：

输出样例：

impossible
1

import java.util.Scanner;public class Main {static int N=1000,n,m,k,INF=1000000000;static int map[][]=new int[N][N];public static void main(String[] args) {// TODO 自动生成的方法存根Scanner sc=new Scanner(System.in);n=sc.nextInt();m=sc.nextInt();k=sc.nextInt();for(int i=1;i<N;i++){for(int j=1;j<N;j++){if(i==j)map[i][j]=0;else map[i][j]=INF;}}for(int i=1;i<=m;i++){int a=sc.nextInt();int b=sc.nextInt();int c=sc.nextInt();map[a][b]=Math.min(map[a][b], c);}tfloyd();for(int i=1;i<=k;i++){int a=sc.nextInt();int b=sc.nextInt();if(map[a][b]>=INF/2)System.out.println("impossible");else System.out.println(map[a][b]);}}static void tfloyd(){for(int k=1;k<=n;k++){for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){map[i][j]=Math.min(map[i][j], map[i][k]+map[k][j]);}}}}
}

1.6 狡兔 k 窟

我是补题链接点我跳转

题目描述

一只兔子名叫小蓝，它异常狡猾，在土中挖了若干洞窟并且设置了很多出入口来应对紧急情况。它一共有 n 个通往地面的出入口，在地面上这 n 个出入口之间由 n − 1 条长度为 1 的双向通路连成一个连通图。第 i 个出入口属于第 ci个洞窟，因此小蓝可以在任意一个属于 ci 的出入口从地面进入洞窟然后从任意一个属于 ci 的出入口跑出到达地面。

小蓝提出了 m 个逃跑路线，第 i 个路线希望从出入口 si 逃往 ti ，它希望在逃跑的过程中在地面上跑动的距离尽可能短，请为每条路线计算逃跑时在地面上跑动的最短距离。

输入格式

输入的第一行包含两个正整数 n, m ，用一个空格分隔。

第二行包含 n 个正整数 c1, c2, · · · , cn ，相邻整数之间使用一个空格分隔。

接下来 n − 1 行，第 i 行包含两个整数 ui, vi ，用一个空格分隔，表示地面上的一条通路连接 ui 和 vi 。

接下来 m 行，第 i 行包含两个整数 si, ti ，用一个空格分隔。

输出格式

输出 m 行，每行包含一个整数，依次表示每个询问的答案。

样例输入

6 3
1 3 2 1 2 3
1 2
1 3
2 4
2 5
3 6
2 6
3 2
4 3

样例输出

0
1
1

提示

对于 20% 的评测用例，1 ≤ n, m, ci ≤ 100 ；

对于所有评测用例，1 ≤ n, m, ci ≤ 5000 ，1 ≤ ui, vi, si, ti ≤ n 。

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.StreamTokenizer;
import java.util.*;public class Main {static int N = 50010, n, m, INF = 1000000000, idx;static int dis[]=new int[N],id[]=new int[N],w[]=new int[N],val[]=new int[N],next[]=new int[N];static boolean flag[];static boolean flag2[]=new boolean[N];static List<Integer> list=new ArrayList<>();public static void main(String[] args) throws IOException {Read sc=new Read();n=sc.nextInt();m=sc.nextInt();Arrays.fill(id,-1);int arr[]=new int[n+1];for(int i=1;i<=n;i++){int num=sc.nextInt();arr[i]=num;}for(int i=0;i<n-1;i++){int a=sc.nextInt();int b=sc.nextInt();add(a,b,1);add(b,a,1);}for(int i=1;i<=n;i++){for(int j=i+1;j<=n;j++){if(arr[i]==arr[j]){add(i,j,0);add(j,i,0);}}}for(int i=0;i<m;i++){int a=sc.nextInt();int b=sc.nextInt();System.out.println(dijk2(a,b));}}static int dijk2(int start,int end){if (start == end) return 0;Arrays.fill(dis,INF);flag=new boolean[N];dis[start]=0;Deque<Integer> queue = new ArrayDeque<>();queue.add(start);while(!queue.isEmpty()){int t=queue.poll();if(t==end)return dis[t];if (flag[t]) continue;flag[t] = true;for(int i=id[t];i!=-1;i=next[i]){int j=val[i];if(dis[j]>dis[t]+w[i]){dis[j]=dis[t]+w[i];if (w[i] == 0) {queue.addFirst(j);} else {queue.addLast(j);}}}}return dis[end];}static void  add(int a,int b,int c){val[idx]=b;next[idx]=id[a];w[idx]=c;id[a]=idx++;}
}
class Read {BufferedReader bfr = new BufferedReader(new InputStreamReader(System.in));StreamTokenizer st = new StreamTokenizer(bfr);public int nextInt() throws IOException {st.nextToken();return (int) st.nval;}public long nextLong() throws IOException {st.nextToken();return (long) st.nval;}public Double nextDouble() throws IOException {st.nextToken();return (Double) st.nval;}public String nextLine() throws IOException {return bfr.readLine();}public String next() throws IOException {return st.sval;}
}

1.7 星际旅行

我是补题链接点我跳转写题

问题描述

小明国庆节准备去某星系进行星际旅行，这个星系里一共有 n 个星球，其中布置了 m 道双向传送门，第 i 道传送门可以连接 ai,bi两颗星球（ai≠bi 且任意两颗星球之间最多只有一个传送门）。

他看中了一款 “旅游盲盒”，一共有 Q 个盲盒，第 i 个盲盒里的旅行方案规定了旅行的起始星球 xi 和最多可以使用传送门的次数 yi。只要从起始星球出发，使用传送门不超过规定次数能到达的所有星球都可以去旅行。

小明关心在每个方案中有多少个星球可以旅行到。小明只能在这些盲盒里随机选一个购买，他想知道能旅行到的不同星球的数量的期望是多少。

输入格式

输入共 m+Q+1行

第一行为三个正整数 n,m,Q

后面 m 行，每行两个正整数 ai,bi

后面 Q 行，每行两个整数 xi,yi

输出格式

输出共一行，一个浮点数（四舍五入保留两位小数）。

样例输入

样例输出

2.00

样例说明

第一个盲盒可以旅行到 1,2,3

第二个盲盒可以旅行到 2

第三个盲盒可以旅行到 1,2

所以期望是 (3+1+2)/3=2.00

评测用例规模与约定

对于 20% 的评测用例，保证 n≤300

对于 100%的评测用例，保证 n≤1000,m≤min⁡{n(n−1)2,5n},Q≤50000, 0≤yi≤n

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.StreamTokenizer;
import java.util.*;
public class Main {static int n,m,k,INF=1000000000,N=2000;static int map[][]=new int[N][N];public static void main(String[] args) throws IOException {Read sc=new Read();n=sc.nextInt();m=sc.nextInt();k=sc.nextInt();for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){if(j==i)map[i][j]=0;else map[i][j]=INF;}}while(m-->0){int a=sc.nextInt();int b=sc.nextInt();map[a][b]=Math.min(map[a][b],1);map[b][a]=Math.min(map[b][a],1);}floyd();int ans=0;int q=k;while(k-->0){int a=sc.nextInt();int b=sc.nextInt();int cnt=0;for(int i=1;i<=n;i++){if(map[a][i]<=b)cnt++;}ans+=cnt;}double endand=(double)ans/q;System.out.println(String.format("%.2f",endand));}static void floyd(){for(int k=1;k<=n;k++){for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){map[i][j]=Math.min(map[i][j],map[i][k]+map[k][j]);}}}}
}
class Read {BufferedReader bfr = new BufferedReader(new InputStreamReader(System.in));StreamTokenizer st = new StreamTokenizer(bfr);public int nextInt() throws IOException {st.nextToken();return (int) st.nval;}public long nextLong() throws IOException {st.nextToken();return (long) st.nval;}public Double nextDouble() throws IOException {st.nextToken();return (Double) st.nval;}public String nextLine() throws IOException {return bfr.readLine();}public String next() throws IOException {return st.sval;}
}

二、模拟

2.1 I Love 1543

这是机翻，觉得不好看请点原题

我是补题链接点我跳转写题

一日早晨，Polycarp 醒来，意识到 1543 是他生活中最喜欢的数字。
Polycarp 当天一睁开眼睛看到的第一件事是一个大小为 n×m 的大墙地毯；n 和 m 是偶数。每个单元格内包含从 0 到 9 的一个数字。
Polycarp 对这个地毯的每一层顺时针遍历时，数字 1543 会出现多少次产生了好奇。
地毯的第一层是定义为一条长度为 2⋅(n+m−2) 且厚度为 1 的封闭带，围绕地毯的外部部分。每一层是通过从原始地毯中去除所有先前的层，得到的地毯的第一层。
输入
输入的第一行包含一个整数 t (1≤t≤100) —— 测试用例的数量。接下来的每一行描述一个测试用例。
每个测试用例的第一行包含一对数字 n 和 m (2≤n,m≤10的3次方，n 和 m 是偶数)。
接下来的 n 行长度为 m，由数字 0 到 9 组成 —— 代表地毯的描述。
保证所有测试用例中，n⋅m 的和不超过 10的6次方。
输出
对于每个测试用例，输出一个整数 —— 地毯的所有层中，数字 1543 顺时针遍历时出现的总次数。
示例
输入
8
2 4
1543
7777
2 4
7154
8903
2 4
3451
8888
2 2
54
13
2 2
51
43
2 6
432015
512034
4 4
5431
1435
5518
7634
6 4
5432
1152
4542
2432
2302
5942
输出
1
1
0
1
0
2
2
2

注意：

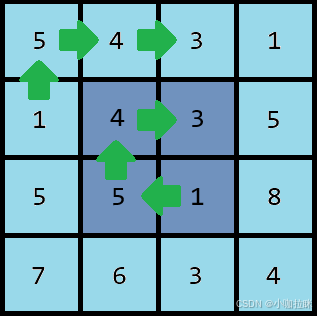
第七个示例中 1543 的出现次数。不同的层使用不同的颜色标记。

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.StreamTokenizer;
import java.util.*;public class Main {public static void main(String[] args) throws IOException {Read sc=new Read();int t=sc.nextInt();while(t-->0){int n=sc.nextInt();int m=sc.nextInt();char map[][]=new char[n][m];for(int i=0;i<n;i++){String s=sc.nextLine();while (s.isEmpty())s=sc.nextLine();map[i]=s.toCharArray();}int ans=0;for(int i=0;i<Math.min(n,m)/2;i++){//层数ArrayList<Character> list = new ArrayList<>();for(int j=i;j<m-i;j++){//右list.add(map[i][j]);}for(int j=i+1;j<n-i;j++){//下list.add(map[j][m-i-1]);}//左for(int j=m-i-2;j>=i;j--){list.add(map[n-i-1][j]);}//上for(int j=n-i-2;j>i;j--){list.add(map[j][i]);}for (int j=0;j<list.size();j++){if(list.get(j)=='1'){if(match(list,j,"1543"))ans++;}}}System.out.println(ans);}}static boolean match(ArrayList<Character> list,int id,String s){for(int i=0;i<s.length();i++){if(s.charAt(i)!=list.get((id+i)%list.size()))return false;}return true;}
}class Read {BufferedReader bfr=new BufferedReader(new InputStreamReader(System.in));StreamTokenizer st = new StreamTokenizer(bfr);public int nextInt() throws IOException {st.nextToken();return (int) st.nval;}public long nextLong() throws IOException {st.nextToken();return (long) st.nval;}public String nextLine() throws IOException {;return bfr.readLine();}
}

2.2分布式队列

我是补题链接点我跳转写题

问题描述

小蓝最近学习了一种神奇的队列：分布式队列。简单来说，分布式队列包含 N 个节点（编号为 0 至 N−1，其中 0 号为主节点），其中只有一个主节点，其余为副节点。

主/副节点中都各自维护着一个队列，当往分布式队列中添加元素时，都是由主节点完成的（每次都会添加元素到主节点对应的队列的尾部）；副节点只负责同步主节点中的队列。可以认为主/副节点中的队列是一个长度无限的一维数组，下标为 0,1,2,3…同时副节点中的元素的同步顺序和主节点中的元素添加顺序保持一致。

由于副本的同步速度各异，因此为了保障数据的一致性，元素添加到主节点后，需要同步到所有的副节点后，才具有可见性。

给出一个分布式队列的运行状态，所有的操作都按输入顺序执行。你需要回答在某个时刻，队列中有多少个元素具有可见性。

输入格式

第一行包含一个整数 N，表示节点个数。

接下来包含多行输入，每一行包含一个操作，操作类型共有以下三种： add、sync 和 query，各自的输入格式如下：

addelement：表示这是一个添加操作，将元素 element添加到队列中;
syncfollowerid：表示这是一个同步操作，followerid号副节点会从主节点中同步下一个自己缺失的元素;
query：查询操作，询问当前分布式队列中有多少个元素具有可见性。

输出格式

对于每一个 query 操作，输出一行，包含一个整数表示答案。

样例输入

3
add 1
add 2
query
add 1
sync 1
sync 1
sync 2
query
sync 1
query
sync 2
sync 2
sync 1
query

样例输出

样例说明

执行到第一个 query 时，队列内容如下：

0： [1,2]

1： []

2： []

两个副节点中都无元素，因此答案为 0。

执行到第二个 query 时，队列内容如下：

0： [1,2,1]

1： [1,2]

2： [1]

只有下标为 0 的元素被所有节点同步，因此答案为 1 。

执行到第三个 query 时，队列内容如下：

0： [1,2,1]

1： [1,2,1]

2： [1]

只有下标为 0 的元素被所有节点同步，因此答案为 1。

执行到第四个 query时，队列内容如下：

0： [1,2,1]

1： [1,2,1]

2： [1,2,1]

三个元素都被所有节点同步，因此答案为 3。

评测用例规模与约定

对于 30% 的评测用例： 1≤输入的操作数 ≤100。

对于 100% 的评测用例： 1≤followerid<N≤2000,1≤N≤10,1≤followerid<N

import java.util.Scanner;public class Main {public static void main(String[] args) {Scanner scan = new Scanner(System.in);int n = scan.nextInt();int a[] = new int[n+1];while (scan.hasNext()) {String s = scan.next();if (s.equals("add")) {int x = scan.nextInt();a[0]++;} else if (s.equals("sync")) {int x = scan.nextInt();a[x] = Math.min(a[0], a[x] + 1);} else {int min = a[0];for (int i = 0; i < n; i++) {min = Math.min(min, a[i]);}System.out.println(min);}}}
}

三、填空题

3.1报数游戏

我是补题链接点我跳转写题

问题描述

小蓝和朋友们在玩一个报数游戏。由于今年是 20242024 年，他们决定要从小到大轮流报出是 2020 或 2424 倍数的正整数。前 1010 个被报出的数是：20,24,40,48,60,72,80,96,100,12020,24,40,48,60,72,80,96,100,120。请问第 202420242024202420242024 个被报出的数是多少?

答案提交

这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

import java.util.Scanner;
// 1:无需package
// 2: 类名必须Main, 不可修改public class Main {public static void main(String[] args) {Scanner scan = new Scanner(System.in);System.out.println(202420242024l/2*24);scan.close();}
}

3.2 类斐波那契循环数

这题目贴出来公式有问题，请跳转写原题

我是补题链接点我跳转写题

问题描述

对于一个有 n 位的十进制数 N=d1d2d3…可以生成一个类斐波那契数列S，数列 S 的前 n 个数为：

{S1=d1,S2=d2,S3=d3,…,Sn=dn}

数列 SS 的第 k(k>n)个数为：

Si=k−n∑k−1Si

如果这个数 N 会出现在对应的类斐波那契数列 S 中，那么 N 就是一个类斐波那契循环数。

例如对于 197，对应的数列 S 为：

{1,9,7,17,33,57,107,197,…}

197 出现在 S 中，所以 197是一个类斐波那契循环数。

请问在 0 至 107中，最大的类斐波那契循环数是多少?

答案提交

这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

import java.util.ArrayDeque;
import java.util.Scanner;public class Main {static ArrayDeque<Integer> deque = new ArrayDeque<>();public static void main(String[] args) {Scanner sc = new Scanner(System.in);for (int i = 10000000; i >= 197; i--) {if (check(i)) {System.out.println(i);break;}deque.clear();}sc.close();}public static boolean check(int n) {int sum = 0, x = n;while (x > 0) {int t = x % 10;if (t != 0) {deque.addFirst(t);}sum += t;x /= 10;}if (deque.size() == 1) return false;deque.addLast(sum);while (!deque.isEmpty() && sum < n) {sum = sum * 2 - deque.pollFirst();deque.addLast(sum);}return sum == n;}
}

3.3 互质

我是补题链接点我跳转写题

问题描述

请计算在 [1,2023的2023次方] 范围内有多少个整数与 2023 互质。由于结果可能很大，你只需要输出对 109+7取模之后的结果。

答案提交

这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

import java.util.Scanner;public class Main {static final int MOD = 1000000007;public static void main(String[] args) {long pow = fastPow(2023, 2022, MOD);long result = (pow * 1632) % MOD;System.out.println(result);}public static long fastPow(long base, long exp, long mod) {long result = 1;base %= mod; while (exp > 0) {if ((exp & 1) == 1) {result = (result * base) % mod;}base = (base * base) % mod;exp >>= 1;}return result;}
}

查看全文

http://www.xdnf.cn/news/155.html