强连通分量:Kosaraju算法
强连通分量:Kosaraju算法
想象一下你正在一个大型购物中心里,商场里有多个出入口,每个出入口都连接着不同的店铺。有些店铺之间是单向通道(比如只能从A到B,不能从B到A),有些则是双向通道。现在,如果我们想知道哪些店铺组成了一个"互相可达"的群体(即从群体中任何一个店铺出发,都能到达群体中的其他所有店铺),这个问题就类似于图论中的强连通分量(Strongly Connected Components, SCC)问题。
在计算机科学中,强连通分量是指有向图中任意两个顶点都能互相到达的最大子图。识别强连通分量在很多领域都有重要应用,比如社交网络分析、编译器优化、网络路由等。今天我们要介绍的Kosaraju算法,就是一种高效寻找强连通分量的方法。
Kosaraju算法由S. Rao Kosaraju在1978年提出,虽然它的时间复杂度与Tarjan算法相同(都是O(V+E)),但它的实现更为直观,更容易理解。让我们一起来探索这个算法的奥秘。
一、算法执行流程
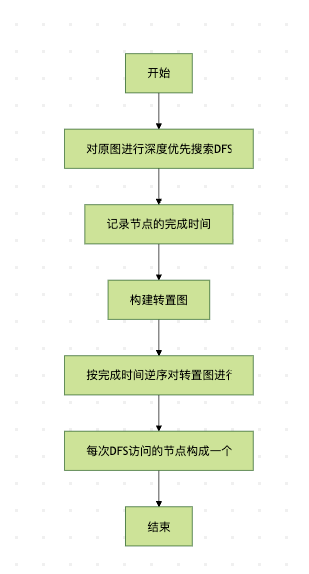
图1:Kosaraju算法的基本流程
理解了基本概念后,我们来看Kosaraju算法的具体执行流程。整个算法可以分为三个主要步骤:
- 第一次DFS遍历:对原图进行深度优先搜索,并在节点完成访问时记录其完成时间(即节点被完全处理的时间点)。
- 构建转置图:将有向图中所有边的方向反转,得到转置图。
- 第二次DFS遍历:按照第一次DFS得到的完成时间逆序,对转置图进行DFS。每次DFS访问的节点就构成一个强连通分量。
这个流程看起来简单,但为什么这样就能找到强连通分量呢?让我们通过一个具体例子来理解。
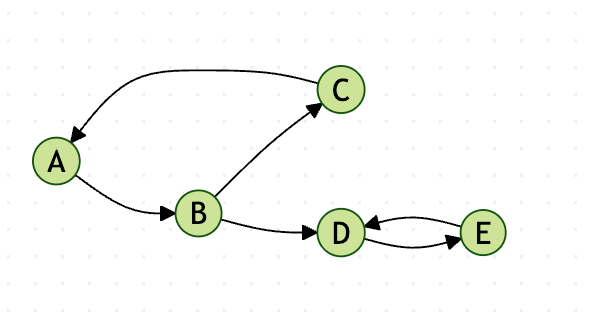
图2:示例有向图
以上图为例,我们可以直观地看到有三个强连通分量:{A,B,C}、{D,E}和{F}。接下来,我们将用Kosaraju算法来找出这些分量。
二、技术原理与实现
现在我们已经了解了算法的基本流程,让我们深入探讨其技术原理和具体实现。Kosaraju算法的关键在于理解为什么在转置图上按照完成时间逆序进行DFS就能找到强连通分量。
算法的核心思想是:强连通分量在转置图中仍然是强连通分量。通过第一次DFS,我们实际上是在对图中的节点进行拓扑排序(虽然不是严格的拓扑排序,因为图中可能有环)。然后在转置图中按照这个顺序进行DFS,可以确保我们首先访问的是"源头"节点,从而正确识别各个强连通分量。
下面是Python实现的完整代码:
from collections import defaultdictclass Graph:def __init__(self, vertices):self.V = verticesself.graph = defaultdict(list)def add_edge(self, u, v):self.graph[u].append(v)def dfs_util(self, v, visited, stack):visited[v] = Truefor neighbor in self.graph[v]:if not visited[neighbor]:self.dfs_util(neighbor, visited, stack)stack.append(v)def get_transpose(self):g = Graph(self.V)for u in self.graph:for v in self.graph[u]:g.add_edge(v, u)return gdef find_scc(self):stack = []visited = [False] * self.V# 第一次DFS,填充完成时间栈for i in range(self.V):if not visited[i]:self.dfs_util(i, visited, stack)# 创建转置图transpose = self.get_transpose()# 重置访问标记visited = [False] * self.Vsccs = []# 按照完成时间逆序处理转置图while stack:v = stack.pop()if not visited[v]:scc = []transpose.dfs_util(v, visited, scc)sccs.append(scc)return sccs# 示例使用
g = Graph(6)
g.add_edge(0, 1) # A->B
g.add_edge(1, 2) # B->C
g.add_edge(2, 0) # C->A
g.add_edge(1, 3) # B->D
g.add_edge(3, 4) # D->E
g.add_edge(4, 3) # E->Dprint("强连通分量:")
for scc in g.find_scc():print(scc)
代码1:Kosaraju算法的Python实现
上述代码首先定义了一个Graph类,包含添加边、DFS辅助函数、构建转置图和查找强连通分量的方法。在示例中,我们创建了与图2对应的有向图,然后调用find_scc()方法找出所有强连通分量。
实现要点:
- 使用邻接表表示图结构
- 第一次DFS遍历记录节点完成时间(使用栈结构)
- 构建转置图时反转所有边的方向
- 第二次DFS按照完成时间逆序进行
算法步骤详解
让我们更详细地分解算法的每个步骤,用之前的示例图来说明:
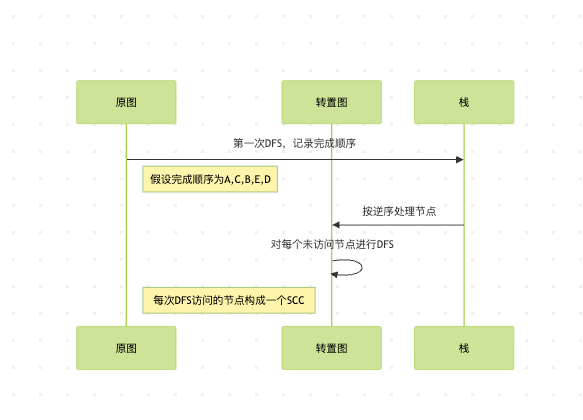
图3:Kosaraju算法的交互流程
-
第一次DFS遍历:
从任意节点开始DFS(假设从A开始),记录节点的完成时间。完成顺序可能是A、C、B、E、D(实际顺序取决于具体的DFS实现)。
这里的关键是,强连通分量中的节点会在连续的时间段内完成。例如,A、B、C会连续完成,因为它们属于同一个强连通分量。
-
构建转置图:
将所有边的方向反转。例如A→B变为B→A,B→C变为C→B,等等。
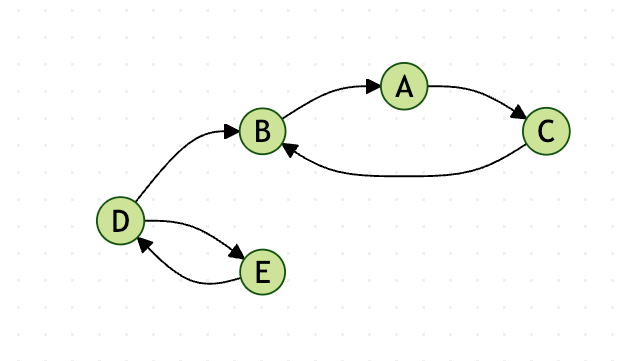
图4:转置图示例
-
第二次DFS遍历:
按照第一次DFS的完成时间逆序处理节点(即D、E、B、C、A)。
从D开始DFS,可以访问D和E,因此{D,E}是一个强连通分量。
接下来处理B(如果未被访问),可以访问B、A、C,因此{A,B,C}是另一个强连通分量。
三、算法正确性分析
理解了算法步骤后,我们不禁要问:为什么这个算法能正确找到所有强连通分量?让我们从数学角度分析其正确性。
关键在于两个观察结果:
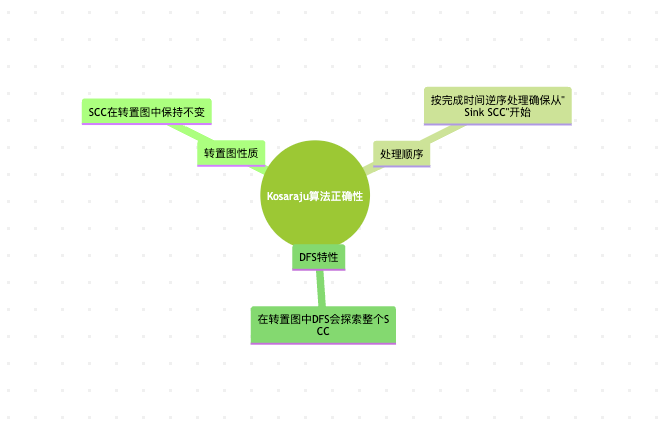
图5:算法正确性分析
-
转置图性质:
强连通分量在转置图中仍然是强连通分量。因为如果原图中u和v互相可达,那么在转置图中它们仍然互相可达(只是路径方向相反)。
-
处理顺序:
按照完成时间逆序处理节点,相当于按照某种"拓扑排序"的逆序处理。这样可以确保我们先处理"汇聚"节点(即没有出边的节点或SCC),在转置图中这些节点就变成了"源头"节点。
-
DFS特性:
在转置图中从一个节点开始DFS,会探索该节点所在的整个强连通分量,因为强连通分量中的节点互相可达,而转置图保持了这种可达性。
通过这种设计,Kosaraju算法能够有效地将图分解为若干个强连通分量。每次在转置图中找到一个未被访问的节点开始DFS,就能发现一个新的强连通分量。
四、算法复杂度分析
在实际应用中,算法的效率至关重要。让我们分析Kosaraju算法的时间和空间复杂度。
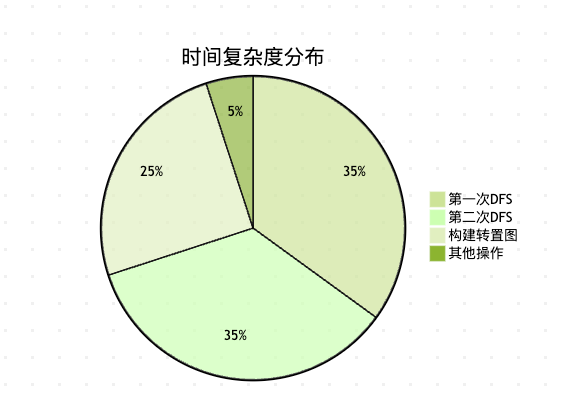
图6:时间复杂度分布
-
时间复杂度:O(V + E)
算法执行两次DFS,每次DFS的时间复杂度都是O(V+E)。构建转置图也需要O(V+E)时间。因此总时间复杂度为O(V+E)。
-
空间复杂度:O(V + E)
需要存储原图和转置图,空间复杂度为O(V+E)。此外还需要O(V)的额外空间用于存储访问标记和栈。
性能优化提示:
- 对于大规模图,可以考虑使用迭代DFS代替递归DFS以避免栈溢出
- 可以使用位操作来压缩访问标记数组,减少内存使用
- 并行化第一次DFS和转置图构建可以提升性能
五、应用场景与比较
理解了Kosaraju算法的原理和实现后,我们来看看它的实际应用场景以及与其他算法的比较。

图7:算法比较与应用场景
与其他算法的比较
| 算法 | 优点 | 缺点 |
|---|---|---|
| Kosaraju | 实现简单,易于理解 | 需要两次DFS和转置图 |
| Tarjan | 单次DFS,效率高 | 实现复杂,需要维护更多状态 |
| Gabow | 类似Tarjan但使用不同数据结构 | 同样实现复杂 |
典型应用场景
- 编译器优化:识别代码中的循环结构,进行优化
- 社交网络分析:发现紧密联系的群体或社区
- 网络路由:分析网络拓扑结构,优化路由路径
- 电子电路设计:分析电路中的反馈回路
- 网页链接分析:识别网页间的紧密连接结构
六、总结
通过今天的讨论,我们深入了解了Kosaraju算法的原理和实现。让我们回顾一下本文的主要内容:
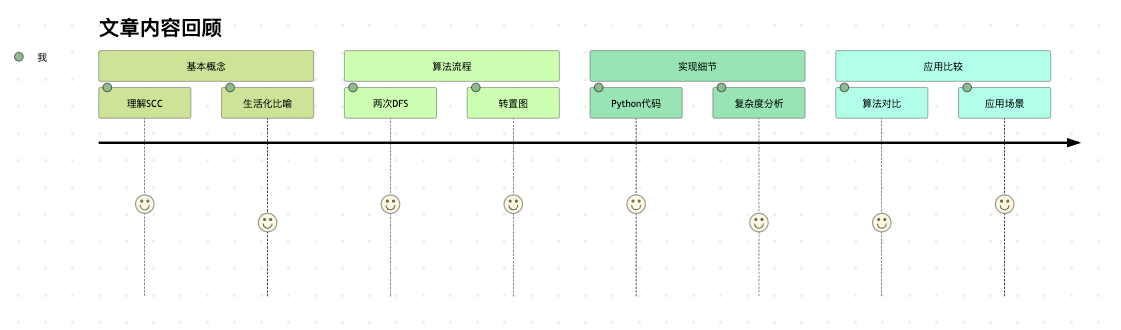
图8:文章内容回顾
- 基本概念:介绍了强连通分量的定义和直观理解
- 算法流程:详细讲解了Kosaraju算法的三个关键步骤
- 技术实现:提供了完整的Python实现代码
- 正确性分析:解释了为什么算法能正确找到所有SCC
- 复杂度分析:评估了算法的时间和空间复杂度
- 应用比较:对比了不同算法,列举了典型应用场景
Kosaraju算法以其简洁性和直观性,成为学习强连通分量问题的绝佳起点。虽然在实际应用中可能会选择更高效的Tarjan算法,但理解Kosaraju算法对于掌握图论基本概念和算法设计思想非常有帮助。
希望大家通过本文的学习,对强连通分量和Kosaraju算法有了更深入的理解。在实际应用中,可以根据具体需求选择合适的算法。如果有任何问题或想法,欢迎随时交流讨论!
