傅里叶变换的基本思想通俗解释与应用介绍
傅里叶变换（Fourier Transform）是信号处理、物理学、工程学等多个领域中非常重要的数学工具。它帮助我们将一个随时间变化的信号（比如声音、电磁波、振动等）从时域转换到频域，从而分析这个信号由哪些频率成分组成。
图1 从不同维度展示信号的傅里叶变换特征情况
目录
一、傅里叶变换的基本思想
二、连续傅里叶变换定义
三、物理意义举例说明
四、离散傅里叶变换（DFT）
五、图示理解
六、应用场景
七、一些常见误区澄清
八、简单例子演示
一、傅里叶变换的基本思想
任何满足一定条件的函数都可以表示为多个不同频率的正弦/余弦波的叠加。
换句话说：
一个复杂的时间信号（如一段音乐、心电信号），可以看作是由许多不同频率、幅度和相位的正弦波组成的。
傅里叶变换的作用就是：把这段“混合信号”拆开，看看里面都有哪些频率成分，以及它们各自的“强度”是多少。
二、连续傅里叶变换定义（数学表达式）
对于一个连续时间信号 𝑓(𝑡)，它的傅里叶变换定义如下：
其中：
- f(t)是原始信号（时域）
- F(ω) 是该信号的频谱（频域）
- ω是角频率（单位：弧度/秒），ω=2πf
- j=−1是虚数单位
是复指数函数，用于提取不同频率的正弦分量
傅里叶逆变换：
如果你已经知道频域的信息 F(ω)，可以通过逆变换还原回时域信号：
三、物理意义举例说明
假设你有一段音乐录音（比如一首歌），用麦克风采集后得到一个电压随时间变化的信号 f(t)f(t)。
通过傅里叶变换 F(ω)，你可以看到：
- 这个信号在哪些频率上有能量（即有哪些音符）
- 每个频率的能量大小（振幅）
- 各频率之间的相对关系（相位）
这就像给信号做了一个“频率体检”，告诉你它是怎么构成的。
四、离散傅里叶变换（DFT）
在实际应用中，我们通常只能获取有限个采样点的数据（例如音频数字化、图像处理），所以更常用的是离散傅里叶变换（DFT）：
其中：
是第 n个采样点- N是总采样点数
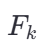是第 k个频率分量的值
计算机实现的快速算法叫做 快速傅里叶变换（FFT），是现代数字信号处理的核心技术之一。
五、图示理解（想象一下）
| 图像 | 内容 |
|---|---|
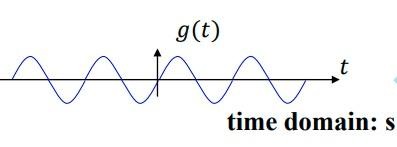 | 一个简单的时域信号（横轴是时间） |
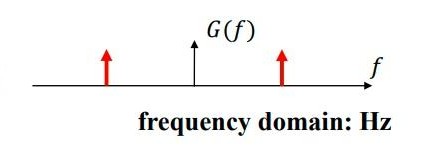 | 经过傅里叶变换后的频域图（横轴是频率） |
在频域图中，每个峰代表一种频率成分，峰的高度代表其强度。
六、应用场景
| 领域 | 应用 |
|---|---|
| 通信系统 | 调制解调：在无线通信中，为了有效传输信息，需要对信号进行调制。傅里叶变换有助于分析和设计这些调制方案，以及实现解调过程。 信道编码：通过分析信道的频率响应，可以设计出更有效的编码和纠错策略，提高通信系统的性能。 |
| 音频处理 | 音频压缩：如MP3格式的音频文件，通过傅里叶变换分析音频信号中的频率成分，去除人耳听不到的高频和低频部分来实现压缩。 噪音消除：使用傅里叶变换可以识别并过滤掉音频信号中的背景噪音，提高音质。 |
| 图像处理 | 图像压缩：JPEG图像格式利用离散余弦变换（DCT），一种与傅里叶变换紧密相关的技术，来压缩图像数据。通过对图像进行二维傅里叶变换，可以分离出重要的频率信息，丢弃不重要的信息以达到压缩的目的。 边缘检测：傅里叶变换可以帮助识别图像中的边缘特征，这对于计算机视觉和图像识别非常重要。 |
| 医学成像 | MRI（磁共振成像）：MRI扫描过程中生成的数据是通过傅里叶变换来重建图像的。原始数据代表的是空间频率的信息，通过逆傅里叶变换将其转换为空间域中的图像。 |
| 金融分析 | 时间序列分析：在金融市场分析中，傅里叶变换被用来分析股票价格、汇率变动等的时间序列数据，以识别其中的周期性和趋势性成分。 |
七、一些常见误区澄清
| 误解 | 正确理解 |
|---|---|
| 傅里叶变换只能处理周期信号 | 不对，非周期信号也可以用，只是频谱变成连续的 |
| 只有实信号才能做傅里叶变换 | 错，复信号（如雷达信号）也适用 |
| FFT 就是 DFT | FFT 是 DFT 的快速实现方法，不是数学定义本身 |
| 傅里叶变换只有工程师才用得上 | 物理、生物、经济等领域都广泛应用 |
八、简单例子演示
假设有一个简单的信号：
其中
对它进行傅里叶变换后，在频域会看到两个明显的峰值，分别出现在 50 Hz 和 120 Hz 处，高度分别为 1 和 0.5。
欢迎大家在学习过程中留言评论，一起讨论交流！