当前位置：首页 > ai >正文

MYOJ_4149:(洛谷P1002)[NOIP 2002 普及组] 过河卒(坐标型DP)

ai 2025/7/17 7:31:49

题目描述

棋盘上 A 点有一个过河卒，需要走到目标 B 点。卒行走的规则：可以向下、或者向右。同时在棋盘上 C 点有一个对方的马，该马所在的点和所有跳跃一步可达的点称为对方马的控制点。因此称之为“马拦过河卒”。

棋盘用坐标表示，A 点 (0,0)、B 点 (n,m)，同样马的位置坐标是需要给出的。

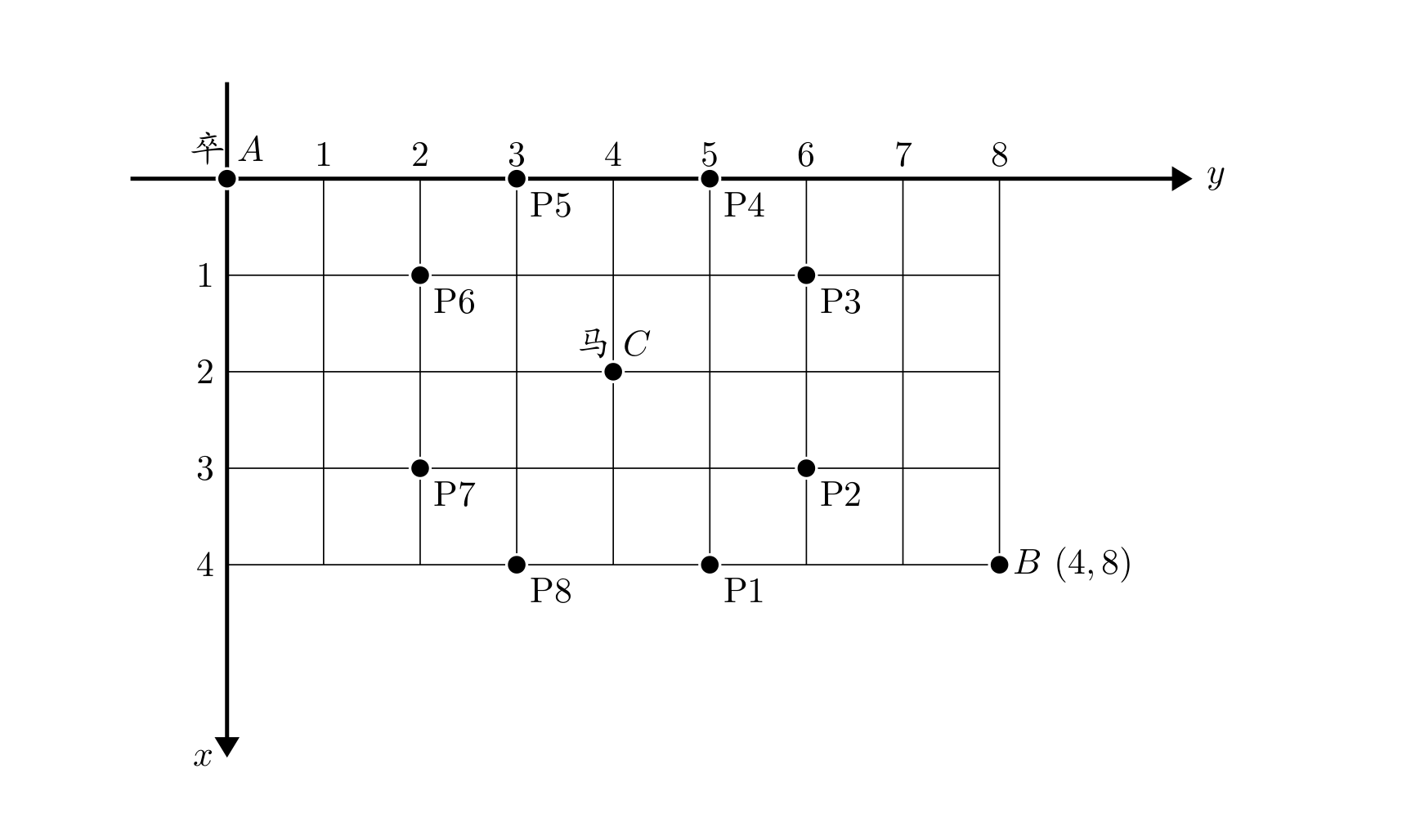
现在要求你计算出卒从 A 点能够到达 B 点的路径的条数，假设马的位置是固定不动的，并不是卒走一步马走一步。

注意：输出可能会很大。

输入

一行四个正整数，分别表示 B 点坐标和马的坐标。

输出

一个整数，表示所有的路径条数。

样例输入输出

输入1：6 6 3 3
输出1：6

输入2：8 6 0 4
输出2：1617

思路：

既然马的位置固定，那么可以确定所有无法到达的点，可以像之前图论一样设置dir8方向数组。

接下来分析。

决策：卒在每一步向右/向下走

策略：从起点(0,0)出发到其中一点(i,j)的一条可行路径

策略集合即从起点(0,0)出发到其中一点(i,j)所有可行路径

得出状态转移方程：起点路径为1条，边界可到达的点：

第一行（i = 0）：dp[0][j] = dp[0][j-1] (只有左方)
第一列（j = 0）：dp[i][0] = dp[i-1][0] (只有上方)
注意，这两行遇到无法到达的点后面久都是0了

其余可到达的点，均为上方到达情况与左方到达情况的加和,即

dp[i][j] = dp[i-1][j] + dp[i][j-1]

并先判断并标记无法到达的点为0

STEP 1:输入，并使用vis数组预先标记无法到达的点。

STEP 2:初始化dp[0][0]=1，并按照状态转移方程标记第0行和第0列

STEP 3:状态转移方程标记剩余点

STEP 4:输出dp[n][m]

代码

#include<bits/stdc++.h>
using namespace std;
long long n,m,hx,hy,dp[25][25],dir[8][2]={{2,1},{2,-1},{1,2},{-1,2},{-1,-2},{-2,-1},{1,-2},{-2,1}};
bool vis[25][25];
int main()
{cin>>n>>m>>hx>>hy;vis[hx][hy]=true;for(int i=0;i<8;i++){vis[hx+dir[i][0]][hy+dir[i][1]]=true;}dp[0][0]=1;for(int i=1;i<=n;i++){if(!vis[i][0]){dp[i][0]=dp[i-1][0];}else{break;}}for(int j=1;j<=m;j++){if(!vis[0][j]){dp[0][j]=dp[0][j-1];}else{break;}}for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){if(!vis[i][j]){dp[i][j]=dp[i-1][j]+dp[i][j-1];}}}cout<<dp[n][m];return 0;
}